激光陀螺捷联惯性导航系统解析对准误差特性分析

陈河， 张志利， 周召发， 刘朋朋， 赵晓枫

(火箭军工程大学 导弹工程学院， 陕西 西安 710025)

0　引言

捷联惯性导航系统(SINS)是一个积分系统，导航解算需要在已知系统初始位置、速度和姿态的基础上进行。SINS的初始姿态通过初始对准获取，对准误差会对导航精度产生直接影响。因此，初始对准的误差分析对算法改进、器件选型和系统精度评估等具有重要指导意义。截至目前，已有很多学者对惯性器件带来的对准误差进行了大量分析，如文献[1-5]分析了惯性器件误差对解析对准的影响，文献[6-7]分析了惯性器件误差对罗经法对准的影响，文献[8-10]推导了惯性器件误差带来的Kalman滤波对准误差，文献[11-15]分析了惯性系粗对准的误差。上述文献的分析表明，不同对准方法中器件常值误差带来的对准误差是一致的。然而，上述研究均着重分析器件常值误差带来的对准失准角，未考虑对准误差的随机特性，也没有分析对准失准角带来的姿态角误差。由于常值误差的影响可以通过器件标定或适当的对准方法(如二位置对准、连续旋转对准等)加以消除[16-18]，实际中更关心的往往是误差的随机特性。对于激光陀螺捷联惯性导航而言，测量输出中除包含常值误差外，还包含随机游走误差，造成对准误差的随机波动。与传统的机械陀螺相比，随机游走误差是光学陀螺特有的性能指标，用于描述陀螺输出的白噪声水平，对初始对准和导航性能有重要影响，尤其是高精度导航系统中，随机游走成为制约对准速度和系统性能的重要因素。文献[19]分析了随机游走对罗经对准方位失准角的影响；文献[20]基于解析法的速率形式分析了陀螺随机游走对方位失准角的影响，但其分析以载体姿态为0的特殊条件为前提，且推导过程不够严密。在很多应用领域如方位瞄准中，关心的往往是失准角带来的姿态角误差，而不是姿态失准角本身。此外，激光陀螺SINS中惯性器件的输出是增量输出而不是速率输出。因此，本文从解析对准法的增量形式出发，推导了器件误差带来的对准误差及其随机特性，并分析由此造成的姿态角误差，特别是方位角误差。

1　解析对准的基本原理

(1)

采用(1)式的优点主要是惯性器件带来的对准失准角最小，且对准结果不受纬度误差的影响[21]。

实际中，激光陀螺SINS的输出往往是角增量和速度增量，采用增量形式计算姿态矩阵的公式为

(2)

2　对准失准角分析

2.1　测量误差分析

根据SINS的比力方程，载体静止时有

gb=-fb.

(3)

比力fb由加速度计测得，经过刻度误差和安装误差补偿后其测量值为

(4)

(5)

采用增量输出时，有

(6)

(7)

(8)

则加速度计增量输出均值的测量误差为

(9)

(10)

静基座对准时ωie的测量值为

(11)

对应的增量输出为

(12)

(13)

(14)

式中：

(15)

2.2　对准失准角分析

为便于分析，设

(16)

(17)

则有

(18)

根据失准角的定义，有

(19)

比较(18)式、(19)式，可得

φ×=-N.

(20)

将(5)式、(11)式代入(17)式，得

(21)

由于误差为小量，保留1阶小量，有

(22)

同理，设r=g×ωie，s=g×ωie×g，则有

(23)

(24)

由(22)式～(24)式可得

(25)

将(25)式代入矩阵N的计算公式，得

(26)

根据(25)式，整理可得

(27)

式中：δgE、δgN分别为δg在导航系的东向和北向分量；δωE为δω在导航系的东向分量。

对比(20)式和(27)式，可得

(28)

同理可以求得采用增量计算公式(2)式时对准失准角为

(29)

2.3　失准角的统计特性

(30)

结合(29)式可知：

(31)

可见对准失准角的数学期望(均值)取决于陀螺仪和加速度计的常值误差。这与文献[1-5]的分析一致。惯性器件的随机游走造成对准失准角的随机变化，下面分析失准角标准差与随机游走系数之间的关系。为便于分析，将(29)式改写为如下矩阵形式：

(32)

式中：

设P(x)表示随机向量x的协方差矩阵，则有

(33)

结合(10)式、(14)式、(32)式、(33)式可以计算出失准角矢量的协方差矩阵，其对角元素为3个失准角的方差，进行开方运算即可得到失准角的标准差。这里直接给出推导结果：

(34)

式中：T为对准总时间，T=nΔt；

综上所述可以看出，由于矩阵A的前两行均为零元素，东向和北向失准角的随机特性不受陀螺仪随机游走的影响，只与加速度计随机游走有关。

3　对准姿态角误差

姿态角的定义与文献[23]一致，则有

(35)

微分可得

(36)

又由

(37)

可得

(38)

将(38)式代入(36)式并整理，可得

(39)

E(δφ)=HE(φ).

(40)

结合(31)式可得

(41)

姿态角误差矢量的协方差矩阵为

P(δφ)=HP(φ)HT.

(42)

结合(10)式、(14)式、(32)式和(33)式可以计算出姿态角误差矢量的协方差矩阵，其主对角线上的元素为3个姿态角误差的方差，对方差进行开方运算即可得到姿态角误差的标准差。

4　仿真与试验

4.1　仿真分析

设对准点位于北纬34.25°，初始姿态角为俯仰角θ=5°，横滚角γ=3°，航向角ψ=50°，采样频率100 Hz(Δt=0.01 s)，惯性器件性能参数如表1所示。将上述参数代入(31)式、(34)式、(41)式、(42)式，可以计算出对准误差的理论值(见表2)，其中标准差1～4对应的对准时间分别为1 min、5 min、10 min和15 min. 从表2中可以发现：由于加速度计的随机游走较小，带来的水平对准随机误差很小；激光陀螺随机游走较大，带来的方位对准误差较大，因此在短时对准时应结合具体精度要求选择满足要求的陀螺仪。

表1　惯性器件参数设置Tab.1　Parameter configurations of inertial sensors for initial alignment simulation

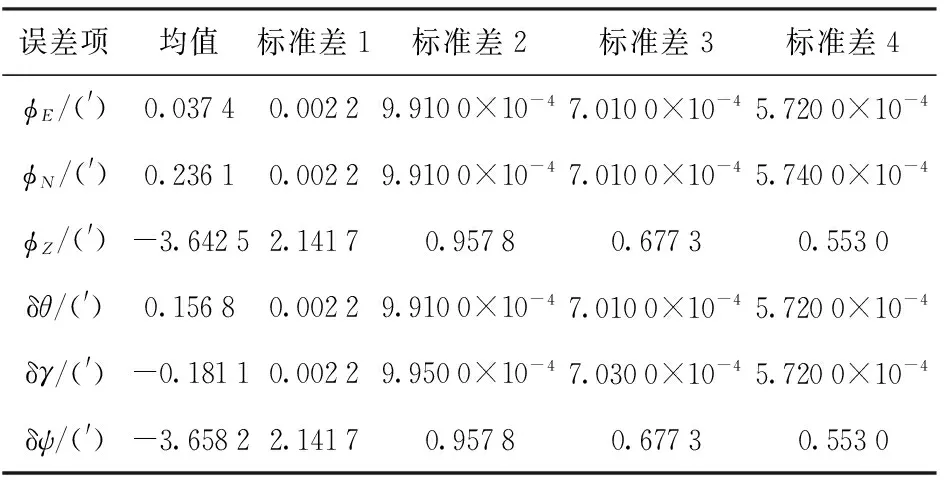
表2　对准误差理论值Tab.2　Theoretical values of initial alignment errors

通过仿真得到SINS在静止基座上的输出结果，然后采用解析法粗对准；在10 s～15 min之间每隔5 s取一个时间值作为对准时间，对每一个对准时间T，分别进行100次对准仿真，计算对准失准角和姿态角误差的均值和标准差。图1是对准时间T从10 s～15 min变化时对应的对准误差理论变化曲线和仿真变化曲线。从图1(a)和图1(c)中可以看出，仿真得到的失准角均值和姿态角误差均值都围绕理论值上下波动，原因在于仿真结果通过计算100次对准失准角的均值得到，本质上也是一个随机变量。从图1(a)和图1(c)中还可以看出，仿真结果绕理论值的波动随对准时间的增长而减小，与理论分析结果一致。从图1(b)和图1(d)中可以看出，误差标准差随对准时间的增长而不断减小，仿真结果与理论分析吻合很好。

对比图1(a)和图1(c)还可以发现，水平失准角φE、φN和水平姿态角误差δθ、δγ明显小于天向失准角φZ和方位角误差δψ. 从(31)式和(41)式可以看出其原因在于，加速度计零偏相对于地球重力加速度的比值(10-5量级)小于陀螺常值漂移相对于地球自转角速度的比值(10-3量级)。此外，水平失准角和水平姿态角误差的大小有明显区别，而天向失准角和方位角误差的大小相差不大。对比(31)式和(41)式可以看出：其原因在于水平失准角和水平姿态误差只与加速度计零偏有关，由于系数矩阵H的作用，二者区别比较明显；而天向失准角和方位角误差计算公式中，陀螺常值漂移项是相同的，区别仅在于加速度计零偏项系数，由于加速度计零偏带来的误差远小于陀螺常值漂移的影响，φZ和δψ相差不大。

分析图1(b)和图1(d)还可以发现：由于加速度计随机游走很小，水平失准角和水平姿态角误差的标准差很小；而天向失准角和方位角误差的标准差则比较大，在对准时间较短时甚至大于其均值。因此对准时水平失准角和姿态角会很快收敛，而天向失准角和方位角则需要较长时间才能收敛到较高精度。由于加速度计的随机游走远小于陀螺的随机游走，(34)式中φZ标准差计算公式中根号内加速度计的随机游走项(10-12量级)远小于陀螺随机游走项(10-5量级)，因此计算天向失准角方差时可以忽略加速度计随机游走的影响，相当于将矩阵B中的-tanL/(gΔt)置0. 计算方位角误差的方差时，同样可以忽略加速度计随机游走的影响，相当于将矩阵H第2行的前两项置0；由于矩阵H第3行的第3项为1，忽略加速度计随机游走影响后φZ和δψ的标准差相等。

4.2　试验验证

为了进一步对理论分析结果进行验证，在实验室转台上进行了相关试验。实验室纬度34.31°，试验中SINS近似处于水平状态；激光陀螺零偏分别为0.005 1°/h、0.004 5°/h、0.003 8°/h，随机游走系数分别为0.000 6°/h1/2、0.001 2°/h1/2、0.000 7°/h1/2；加速度计零偏分别为54 μg、62 μg、57 μg，由于加速度计随机游走很小，试验分析中未予考虑。误差的理论值可以根据试验地点的纬度和惯性器件的误差参数计算出来。可以采用高精度的陀螺经纬仪寻北结果作为方位角真值来计算对准方位误差，而俯仰角和横滚角真值难以获取；由于难以得到SINS的真实姿态矩阵，对准失准角真值也难以获取。试验时仅对方位角误差进行了验证。

方位角误差随时间的变化曲线如图3所示。图3中，试验误差由实际对准得到的方位角均值减去寻北仪测量得到的方位角得到；计算方位角误差理论值时，采用对准得到的姿态矩阵代替真实姿态矩阵进行计算；误差均值和标准差均采用7次试验数据计算得到。试验中SINS保持静止不动，启动系统5 min后开始采集数据，共采集7组数据，每组数据采集10 min，整个试验过程中系统不断电。

从图3(a)中可以看出，方位角误差均值随时间变化曲线与理论曲线也基本吻合，但由于试验中难免引入干扰因素的影响，对准时间较短时方位角误差均值与理论值存在较大偏差；从图3(b)可以看出，方位角误差标准差变化曲线与理论分析结果吻合很好。

方位角误差随SINS方位角的变化如图4所示。图4中误差均值和标准差为7次试验计算得到的结果。试验时系统固定在转台上并近似调平，转动转台使系统指向北附近，启动系统5 min后开始采集数据，共采集7组，每组数据采集1 min；然后依次使转台顺时针转过15°，共24个位置，转到每个位置均使系统静置5 min后采集7组1 min时长的数据；整个试验过程中系统不断电。

从图4中可以看出，试验结果与理论分析结果基本吻合。图4中试验曲线与理论曲线的偏差来源于两个方面：一是试验中干扰因素的影响；二是每个位置试验仅进行了7次，样本较小，导致误差均值和标准差的计算难以达到很高精度。

5　结论

本文对激光陀螺SINS解析法对准的误差进行了分析，推导了惯性器件误差带来的对准失准角及对应的姿态角误差，并分析了其均值和标准差的变化规律。所得主要结论如下：

1)惯性器件误差带来的对准误差均值与对准时间无关，但对准误差标准差与对准时间的平方根呈反比。

2)水平对准误差主要受加速度计精度影响，由于加速度计零偏和随机游走系数一般较小，水平对准可快速达到较高精度。

3)方位对准误差主要受激光陀螺精度影响，激光陀螺随机游走造成的方位对准标准差可达角分级，需要结合对准时间要求选择满足精度的器件。

4)对准误差均值和标准差会随载体姿态角的不同而产生明显改变，实际应用中应通过对惯性器件和对准时间的合理选择来保证任何姿态下对准精度均满足使用要求。

本文主要考虑了惯性器件精度对初始对准的影响，通过(31)式、(34)式、(41)式、(42)式计算出的结果可视为SINS能达到的极限精度，用来对系统和算法性能进行评估。虽然本文着重分析的是惯性器件误差对对准结果的影响，但其他误差(安装误差、刻度误差、外界干扰等)可以等效为器件测量误差，因此采用本文的思路可以分析其对初始对准精度的影响。

参考文献(References)

[1]Britting K R. Inertial navigation system analysis[M]. New York，NY，US: Wiley Interscience, 1971.

[2]Jiang Y F. Error analysis of analytic coarse alignment methods[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 334-337.

[3]周琪, 秦永元, 赵长山. 小角度晃动干扰下解析粗对准的误差分析[J]. 系统工程与电子技术, 2010, 32(7): 1493-1496.

ZHOU Qi, QIN Yong-yuan, ZHAO Chang-shan. Error analysis of analytic coarse alignment on gentle swaying disturbance base[J]. Systems Engineering and Electronics, 2010, 32(7): 1493-1496.(in Chinese)

[4]Li J L, Fang J C, Du M. Error analysis and gyro-bias calibration of analytic coarse alignment for airborne POS[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(11): 3058-3064.

[5]Silva F O, Hemerly E M, Filho W C L. Error analysis of analytical coarse alignment formulations for stationary SINS[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(4): 1777-1796.

[6]徐博, 陈春, 郝燕玲, 等. 动基座捷联罗经初始对准误差分析[J]. 系统工程与电子技术, 2013, 35(4): 812-819.

XU Bo, CHEN Chun, HAO Yan-ling, et al. Error analysis of strapdown compass alignment in dynamic environment[J]. Systems Engineering and Electronics, 2013, 35(4): 812-819. (in Chinese)

[7]高伟, 奔粤阳, 李倩. 捷联惯性导航系统初始对准技术[M]. 北京： 国防工业出版社, 2013.

GAO Wei, BEN Yue-yang, LI Qian. Initial alignment for strapdown inertial navigation system[M]. Beijing: National Defense Industry Press, 2013. (in Chinese)

[8]Cho S Y, Lee H K, Lee H K. Observability and estimation error analysis of the initial fine alignment filter for non-leveling strapdown inertial navigation system[J]. Journal of Dynamic Systems, Measurement, and Control, 2013, 135(3): 021005-1-021005-9.

[9]何昆鹏, 王晓雪. 重力扰动对高精度惯性导航初始对准的影响与补偿[J]. 导航与控制, 2015, 14(5): 84-88.

HE Kun-peng, WANG Xiao-xue. Application of an improved adaptive Kalman filter algorithm in initial alignment of inertial navigation system[J]. Navigation and Control, 2015, 14(5): 84-88.(in Chinese)

[10]Silva F O, Hemerly E M, Filho W C L. On the error state selection for stationary SINS alignment and calibration Kalman filters[J]. Aerospace Science and Technology, 2017, 61(2): 45-56.

[11]孙枫, 曹通. 基于重力信息的惯性系粗对准精度分析[J]. 仪器仪表学报, 2011, 32(11): 2409-2415.

SUN Feng, CAO Tong. Accuracy analysis of coarse alignment based on gravity in inertial frame[J]. Chinese Journal of Scientific Instrument, 2011, 32(11): 2409-2415. (in Chinese)

[12]吴枫, 秦永元, 周琪. 间接解析自对准算法误差分析[J]. 系统工程与电子技术, 2013, 35(3): 586-590.

WU Feng, QIN Yong-yuan, ZHOU Qi. Error analysis of indirect analytic alignment algorithm[J]. Systems Engineering and Electronics, 2013, 35(3): 586-590. (in Chinese)

[13]高薪, 卞鸿巍, 王荣颖, 等. 捷联惯导惯性系对准误差分析[J]. 海军工程大学学报, 2014, 26(6): 42-46.

GAO Xin, BIAN Hong-wei, WANG Rong-ying, et al. Error analysis of coarse alignment for SINS inertial frame[J]. Journal of Naval University of Engineering, 2014, 26(6): 42-46. (in Chinese)

[14]Xu T H, Chang G B, Wang Q X, et al. Analytical 3D rotation estimation using vector measurements with full variance-covariance matrix[J]. Measurement, 2016, 98(2): 131-138.

[15]Chang G B, Xu T H, Wang Q X. Error analysis of Davenport’s q method[J]. Automatica, 2017(75): 217-220.

[16]Song T X, Li K, Wang L, et al. A rapid and high-precision inertial alignment scheme for dual-axis rotational inertial navigation system[J]. Microsystem Technology, 2017, 23(12): 5515-5525.

[17]Du S, Sun W, Gao Y. Improving observability of an inertial system by rotary motions of an IMU[J]. Sensors, 2017, 17(4)：698.

[18]Zhang Y J, Zhou B, Song M L, et al. A novel MEMS gyro north finder design based on the rotation modulation technique[J]. Sensors, 2017, 17(5): 973-994.

[19]张娟秀, 葛磊, 王亚凯. 随机游走对罗经方位对准的影响分析[J]. 中国惯性技术学报, 2017, 25(1): 28-32.

ZHANG Juan-xiu, GE Lei, WANG Ya-kai. Effect of angle random walk on compass azimuth alignment[J]. Journal of Chinese Inertial Technology, 2017, 25(1): 28-32. (in Chinese)

[20]杨俊峰, 司文杰. 陀螺随机游走对导弹自瞄准精度的影响[J]. 航天控制, 2012, 30(5): 21-24.

YANG Jun-feng, SI Wen-jie. The effect of gyro random walk during the process of initial alignment of missile[J]. Aerospace Control, 2012, 30(5): 21-24. (in Chinese)

[21]严恭敏, 严卫生, 徐德民, 等. 纬度未知条件下捷联惯性导航系统初始对准分析[J]. 航天控制, 2008, 26(2): 31-34.

YAN Gong-min, YAN Wei-sheng, XU De-min, et al. SINS initial alignment analysis under geographic latitude uncertainty[J]. Aerospace Control, 2008, 26(2): 31-34. (in Chinese)

[22]Zhao H Y, Shang H, Wang Z L, et al. Comparison of initial alignment methods for SINS[C]∥Proceedings of the 8th World Congress on Intelligent Control and Automation. Taipei，China：IEEE, 2011: 42-47.

[23]秦永元. 惯性导航[M]. 第2版. 北京：科学出版社, 2014.

QIN Yong-yuan. Inertial navigation[M]. 2nd ed. Beijing: Science Press, 2014. (in Chinese)