基于有偏Logistic分布的回归建模及其Score检验

房钦钦，赵为华

（南通大学理学院，江苏南通226019）

0　引言

标准Logistic回归模型中，实际数据是在峰度和平均值相等频率情况下进行分析，然而在实际问题中，数据中因变量的不对称性或不平衡会导致统计分析中的均方误差提高，模型效果也会下降，最后所得到的数据结论也许会与实际情况相差很大，为此，本文引用了偏态参数，该参数值体现了数据的分布偏度情况，利用这一参数在标准Logistic分布的基础上构造了有偏Logistic分布。先对有偏Logistic分布进行简单地研究。

有偏Logistic分布[1]的密度函数为f(x;α)=它的分布函数为F(x;α)=偏态参数。以上记为第一类有偏Logistic分布。

还有一类有偏Logistic分布函数为F(x;α)=1-应的概率密度函数为f(x;α)=为第二类有偏Logistic分布。

由图1和图3可以看出：第一类有偏Logistic分布的偏态参数α取值越大，分布函数会越来越接近1。第二类有偏Logistic分布函数的情况正好相反。

由图2和图4可以看出：密度函数图中，偏态参数α∈(0,1)时，一类有偏Logistic分布为左偏，α＞1时，一类有偏Logistic分布为右偏。而二类有偏Logistic密度分布函数的情况也正好相反。

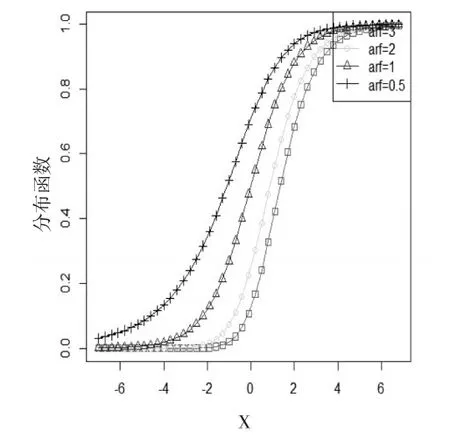
图1四种α不同值的一类有偏函数图

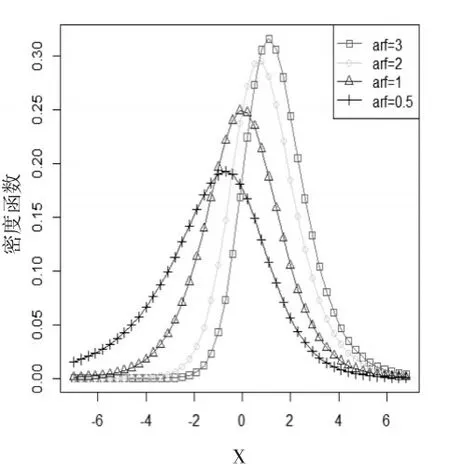
图2四种α不同值的一类有偏密度函数图

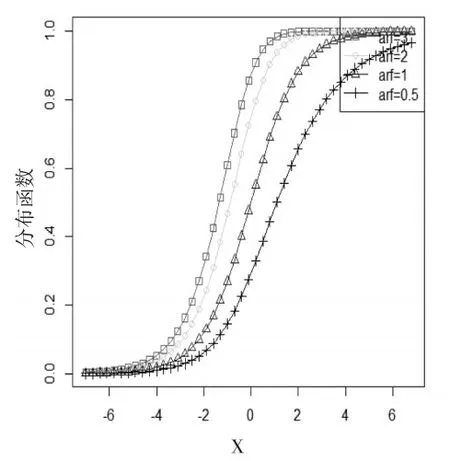
图3四种α不同值的二类有偏函数图

图4四种α不同值的二类有偏密度函数图

1　有偏Logistic分布回归模型以及参数估计

通过前面了解到了两类有偏Logistic分布函数与密度函数的特点。为了探讨基于有偏Logistic分布回归模型在实际数据上的运用，本文建立两类有偏Logistic分布回归模型[2]，并对参数进行估计。

令yi～LG(μi,σi),μi=β，σi=exp(zγ)，i=1,2,...,n,β=(β1,β2,...,βp)T是p×1的位置模型的未知参数向量，γ=(γ1,γ2,...,γq)T是q×1的尺度模型的位置参数向量，xi与zi分别为对应yi位置和尺度部分的解释变量。

两种模型可表示为：

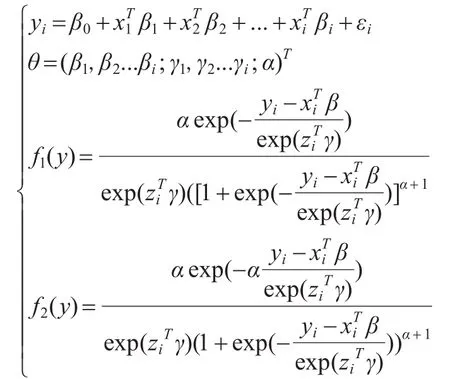
利用牛顿迭代法实现计算，并对参数进行估计。算法[3]如下：

步骤二：给定当前值实现迭代θ(k+1)=θ(k)-H-1(θ(k))S(θ(k))。

步骤三：重复第二步直到收敛条件满足。

从模型中产生模拟数据，用以下三个均方误差用来评价估计的好坏为：

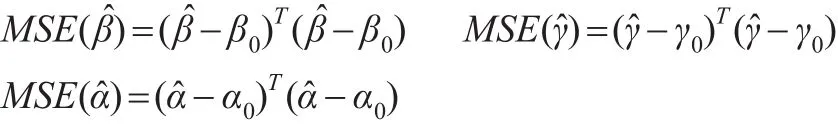
一类有偏Logistic分布的似然函数为：

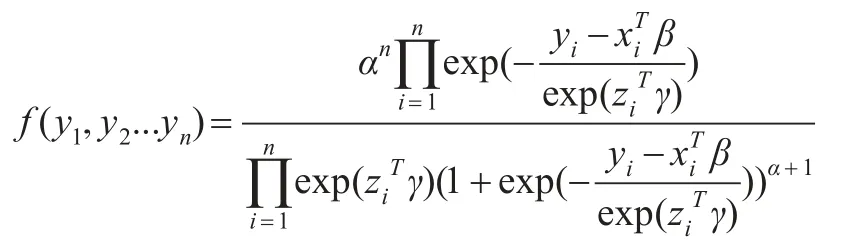
对数似然函数为：

二类有偏似然函数为：

2　数值模拟

下面，通过随机模拟来说明估计方法的有效性。

因为有偏Logistic分布中F(X)～U(0,1)，所以本文首先由y*～U(0,1),n=50,100...，xi～N(0,1)生成随机数，并由逆函数法可得yi=F-1(y*)～L(μ,σ)，由最小二乘法得到参数的估计初值，再经过牛顿迭代法进行收敛，得到参数估计，和。其中两类有偏分布的逆函数分别为

利用牛顿迭代法，在α=0.5，γ=(1,0.5,-1)T，β=(0.5,-0.8)T和α=1.5，γ=(1,0.5,-1)T，β=(0.5,-0.8)T两种情况下，xi和zi的分量独立产生于N(0,1)，进行200次模拟实验。模拟结果见表1。

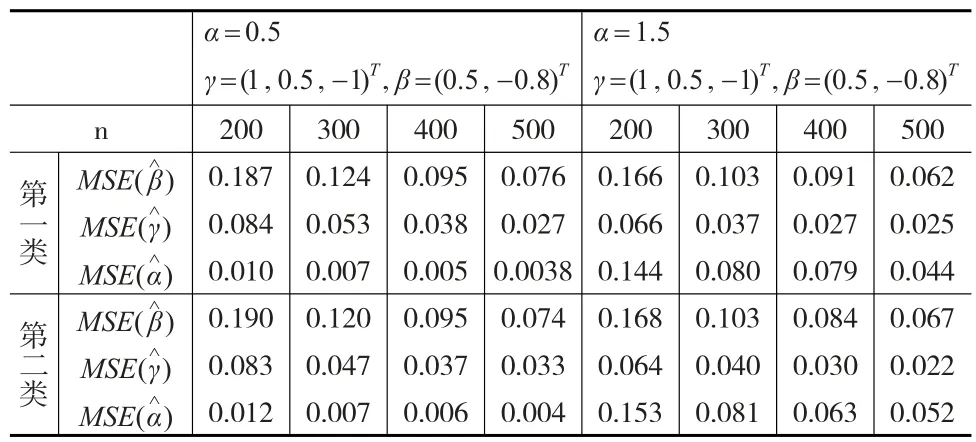
表1　两种有偏Logistic分布参数估计的均方误差表

从表1可以知道，在这两种类型的有偏Logistic位置与尺度模型中，参数的均方误差随着样本量n的增加越来越小，说明了模拟方法的效果越来越好。

3　参数的Score检验及其功效

在实际回归建模时，需要评价模型的正确性和模型中自变量的重要性。为此本文应用Score检验统计量对参数的重要性进行检验，并通过随机模拟来说明检验统计量的检验功效。

在这两类回归模型中，应用Score检验统计量[4]主要对有偏参数α的重要性进行检验。假设H0:α=1；H1:α≠1。若表示原假设H0下的限制最大似然估计，则关于H1的为Fisher信息阵[5]，Iαα为观测Fisher信息阵的逆矩阵对应参数α=1的分块矩阵。由渐近性质可知，检验统计量SC渐近服卡方分布χ2(1)。

下面探讨Score检验统计量的检验功效问题。在数据生成时，对α=1，其他参数β=(1,0,-1)T,γ=(0.5,1)T保持不变的情况下，分别取α=0.4，0.6，0.8，0.9，1，1.1，1.2，1.4和1.6时，考察检验统计量SC的检验功效，在显著性水平0.05下，计算1000次模拟中拒绝原假设H0的比例。

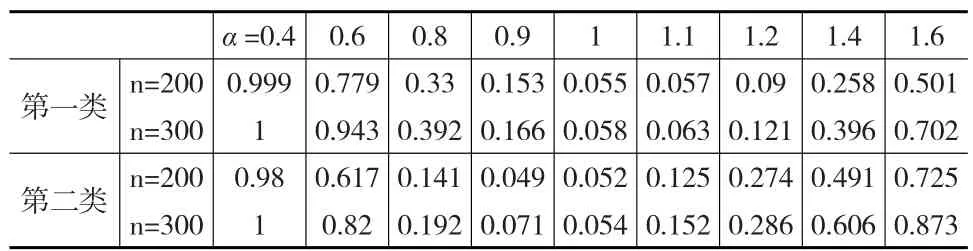
表2　两种有偏Logistic分布α参数检验比例表

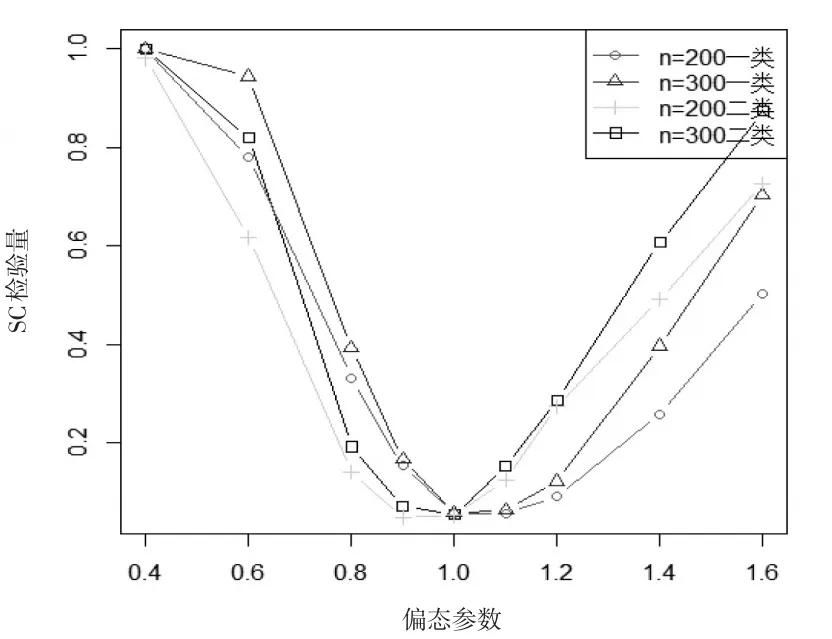
图5　参数α的检验功效图

从表2和图5中可以看到，对H1:α≠1,α＞0，在α→0,α∈(0,1)，Score检验量趋近于1；在α→+∞,α∈(1,+∞)，Score检验量也趋近于1，趋近速度小于α∈(0,1)时的速度；而当α=1时，Score检验量接近于名义水平0.05。也说明了Score检验统计量对该参数的检验是有效的。

当然，也可以对位置和尺度两个参数进行功效检验，受篇幅限制，在此仅对第一类有偏Logistic位置-尺度模型中β进行Score检验。

取β=(1,-1,0)T，其他参数γ=(0.5,1)T，α=0.5;α=1.5保持不变的情况下，假设H0:β2=0；H1:β2≠0，分别取β2=0，0.2，0.4，0.6，0.8和1时，考察其检验统计量的检验功效，即在显著性水平0.05下，计算300次模拟中拒绝原假设H0的比例。

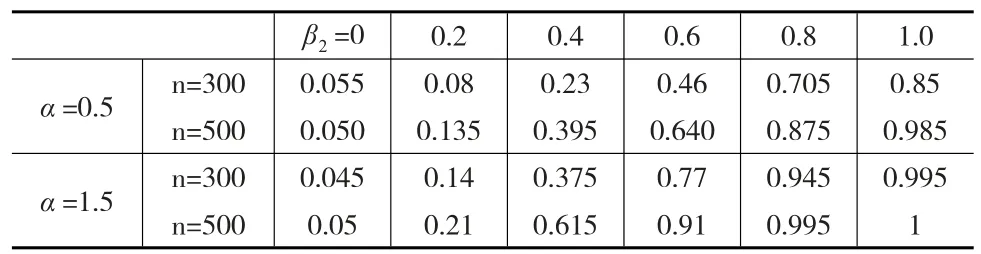
表3　第一类有偏Logistic分布β参数检验比例表

从表3可以看到，无论偏态参数α为何值(α＞0)，在相同的样本量下，随着参数β2的取值远离0时，检验的功效显著增加；另一方面，随着样本量的增大，检验的功效迅速接近于1，且在原假设正确时(β2=0)，检验的功效非常接近于名义水平0.05。

4　实例分析

为了探究经济中产出与投入之间的关系，将上述模型应用于一组希腊1961—1987年制造业的数据中，该数据来自《计量经济学基础上册（第五版）》，“资本”作解释变量x1，“劳动”作解释变量x2，“产出”作因变量y，分析资本和劳动对产出的影响（产出以1970年不变价格的十亿德拉克马计，劳动以每千人计）。

图6至图8为资本、劳动和产出三种变量的箱形图。

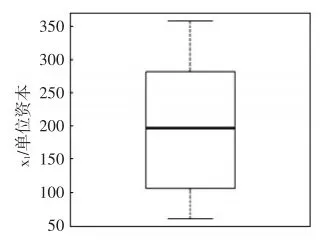
图6资本箱线图

图7劳动箱线图

图8产出箱线图

由图6至图8可知，劳动x2和产出y分布呈现左偏态，都集中在较大值的一侧，而资本x1中位数无偏离情况。可以猜测劳动x2对产出y的影响较大。

在第一类有偏Logistic回归模型中位置、尺度和偏态参数分别为=(-64.25,0.164,0.139)T,=(-9.154,-0.017,0.016)T,=6.63，于是得到的回归方程为=-64.25+0.164x1+0.139x2，此方程说明了每增加一单位资本，则多1.64亿德拉克马的产出；每增加一千人的劳动，会多产1.39亿德拉克马，该结果表明了这与先前的猜测不符合，为此第二次猜测偏态参数对结果有影响。所以对偏态参数进行Score检验，求得SCα=18.356＞χ2(1)=3.84，这证实了本文的第二猜测：偏态参数α对该回归模型结果有显著影响，。

为了从这两种模型和标准Logistic回归模型以及线性回归模型中选择最优模型，利用AIC信息准则和BIC信息准则：

其中k为参数的个数，log(L)为对数似然函数，n为样本量。两种准则是衡量模型拟合好坏的标准，它们的值越小，说明模型对数据拟合得越好。三种模型的计算结果为：

由下页表4和表5可以看到，对于所应用的实例数据，从AIC信息量、BIC信息量和标准差估计三个方面比较，都能得到二类有偏Logistic回归模型拟合程度最高，两类有偏Logistic回归模型都比标准Logistic回归模型模拟得好，且三种Logistic回归模型比用最小二乘法的线性回归模型模拟得好。

表4　四种模型AIC和BIC信息准则量

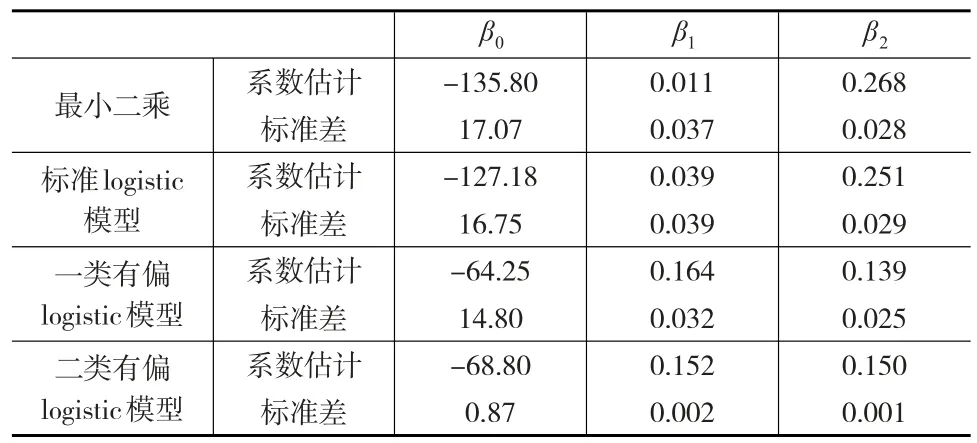
表5　四种模型所求参数估计值

5　总结

本文从两种Logistic回归模型的建立、模型的数据模拟、Score检验统计量、实例运用这几个方面叙述和论证，说明了基于该分布的回归模型对数据能够进行有效的分析。本文也将这两种模型和标准Logistic分布回归模型以及线性回归应用于同一实际案例，并利用AIC和BIC信息准则选择出了最优模型。大量数值模拟和实例数据分析验证了所提方法的有效性，并且得出了结论：基于有偏Logistic分布的回归模型比最小二乘法的线性回归模型和标准Logistic分布回归模型能更好地分析复杂型数据。

参考文献：

[1]史小康,常志勇.两类有偏logistic分布在信用评分模型中的应用[J].统计与决策,2015,(14).

[2]李玲雪,吴刘仓,邱贻涛.Logistic分布下联合位置与尺度模型[J].统计与决策,2014,(20).

[3]吴刘仓,李会琼.极值分布下联合位置与散度模型的变量选择[J].工程数学学报,2012,29(5).

[4]Xie F C,Lin J G,Wei B C.Diagnostics for Skew-normal Nonlinear Regression Models With AR(1)errors[J].Computational Statistics and Data Analysis,2009,(53).

[5]史道济.马尔科夫链的Fisher信息阵及参数的最大似然估计[J].天津大学学报,1993,(3).