基于估计稳定性的变系数模型选择

吕晓玲，刘撷芯，戴秀红

（中国人民大学a.应用统计研究中心；b.数据挖掘中心；c.统计学院，北京100872）

0　引言

变系数模型最初由Hastie和Tibshirani（1993）[1]提出，是一类非常重要的非参数回归模型。它考虑了指示变量与协变量之间的交互效应，与常规的线性模型相比具有更强的适应性和解释性。它在计量经济、生物统计、社会科学等多个领域中都有着广泛的应用，已成为处理多元非参数、半参数回归问题的有力工具[2-4]。

在对实际问题进行回归建模时，为了减小可能存在的模型误差，研究者在初始建模时往往会引入很多可能与被解释变量相关的协变量。但为了提高模型的预测精度、增强模型的可解释性，研究者需要判别对因变量具有显著影响的重要变量。因此，变量选择已成为当今统计分析中一个重要的研究课题。各种各样的正则化估计方法应运而生，也即在传统损失函数的基础上加入惩罚函数，从而实现变量选择和参数估计的同时进行。

与其他正则化估计方法一样，在对变系数模型的正则化估计中，调节参数的选择至关重要。常用的选参准则包括交叉验证（Cross-validation,CV）、贝叶斯信息准则（Bayesian Information Criterion,BIC）、赤池信息量准则（Akaike Information Criterion,AIC）等，这些方法在判别显著变量、提高模型预测准确性等多个方面都非常有效。不过，这些方法所确定的模型或多或少都不具有稳定性，尤其是在高维数据设定下。对此，Lim和Yu（2013）[5]针对线性模型的LASSO问题中正则化参数的选择提出了ESCV（estimation stability cross validation）方法，这一方法有效弥补了以往选参方法在高维数据分析中不稳定这一不足。因此，本文将ESCV方法作为一种选参准则引入到变系数模型的正则化估计中，以期提高变系数模型的稳定性。

1　变系数模型及KLASSO估计

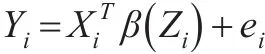
其中ei∈R1是随机噪声，满足E(ei|Xi,Zi)=0，系数向量β(z)={β1(z),...,βd(z)}T∈Rd是未知的，并且是Z的光滑函数。其真实值可给定为β0(z)={β01(z),...,β0d(z)}T∈Rd。不失一般性的假定存在整数d0≤d，对于任意的j≤d，有0＜E{(Z)}＜∞，但对于任意的j＞d，0i0E{(Z)}=0，简单来说，就是假定前d个预测变量与响i0应变量是真实相关的，其余的是不相关的。

Wang和Xia（2013）[4]提出的KLASSO（Kernel Lasso）估计，是一种将流行的核光滑方法与加罚估计结合起来的估计方法，其基本思想是将一个典型的收缩方法即LASSO算法的局部连续核估计应用于变系数模型，KLASSO估计方法如下：

对于任意的指标变量Zi∈[0,1]，β(z)可以通过最小化下面的局部加权最小二乘函数来估计：

对于B0={β0(Z1),…,β0(Zn)}T∈Rn×d，可通过最小化如下全局最小二乘函数来估计：

注意到，在模型假设下，矩阵B0的最后(d-d0)列应该都是0，因此变量选择就等价于在矩阵B0中辨别出稀疏列。借用Yuan和Lin（2006）[6]提出的Group LASSO的方法来判别稀疏列，提出下面的加罚估计：

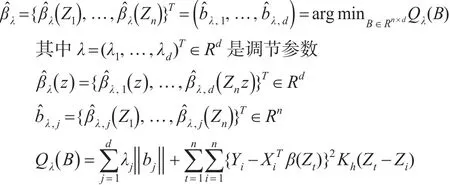
其中，bj是B的第j列，‖.‖表示常用的欧几里德范数。Wang和Xia（2013）[4]使用局部二阶近似算法得到上述估计的解，并证明了KLASSO方法有很好的理论性质。

上述方法涉及到调节参数（核函数K的窗宽h以及惩罚函数的λj,1≤j≤d）的选择问题。文中第一步使用了留一交叉验证方法选取h，然后简使用BIC准则选取λ0。

2　基于估计稳定性的新的变量选择方法

估计稳定性对于一个合理的估计过程来说是一个必要的性质，如果随着样本的不同，估计的值变动相当大，那么这个估计是没有意义的[5，7]。当用L2误差来度量不同样本间的差异时，估计稳定性显然与方差相关，然而在统计学上人们倾向于用稳定性而非变异性来形容不同条件和环境对所估计模型的影响，这就是说稳定性是一个比方差或者变异性更广泛的概念。现有文献中研究变系数模型变量选择和估计方法的文章很多，但是研究变系数模型稳定性的文章却很少。然而模型稳定性对于任何模型来说都是重要的，尤其是在数据采集技术及数据存储技术日益强大的今天，人们经常可以收集到非常多的变量和样本数据，数据往往呈现海量或高维的形态。在分析这些大数据和高维数据时，统计方法的不稳定性出现得更为普遍。

在对有限样本且无模型假定的数据建模时，交叉验证（CV）是建模常用方法，它依赖数据重抽样来评估候选模型的预测误差。具体做法是：在给定的建模样本中，拿出大部分样本作为训练集建立模型，留小部分样本作为测试集，用训练集所建立的模型对预测集进行预测，并求出测试样本的预测误差，记录它们的误差平方和，这个过程一直进行，直到所有的样本都被作为测试集测试了一次而且仅被测试一次时，选出预测误差平方和最小的模型作为最终模型。交叉验证的目的是为了得到可靠稳定的模型，然而，数据重抽样会引发模型的不稳定性，尤其是数据为大数据或者高维数据时。在正则化估计如LASSO估计方法中经常用CV方法来选择调节参数，然而CV通常会导致模型不稳定，从而不利于可靠性解释。Lim和Yu（2013）[5]提出了ESCV方法，即将数据可信度需求加入到交叉验证中，ESCV是一个基于估计稳定性ES（Estimation stability）并将其与CV结合起来的一种无需模型假定的变量选择方法。

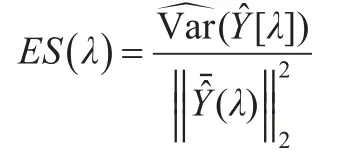
在变系数模型KLASSO估计实际计算中，需要选择合适的调节参数，调整参数的选择在加罚估计的变量选择过程中起着极其重要的作用。当调整参数λ=0时,所有的变量都被选进模型；当调整参数λ=∞时,那么模型中不含有任何变量。λ起到了控制模型复杂度的作用。λ取值越大，得到的模型越简单。反之，λ取值越小，得到的模型越复杂。大的λ给出的估计的方差比较小,而小的λ对应的模型偏差会比较小。因此，在KLASSO估计中调节参数λ的确定对模型的稳定性有重要影响，估计方差和模型偏差之间一个好的平衡就需要选出一个比较理想的λ，如何选择一个合适的调整参数使得模型在预测性和解释性上都能达到一个理想结果就成为人们所关心的重要问题。

Wang和Xia（2009）[4]提出的变系数模型的KLASSO估计中，确定收缩参数λ，是采用BIC最小准则，BIC虽然易于计算，但其有效性依赖于模型假定，而且它是渐近性结果，因此在样本量有限的情况下，BIC模拟结果表现不一定很好，且BIC在统计性能上是不稳定的[8]，当数据是高维数据时，即样本量n小于变量维度p时，Lim和Yu（2013）[5]将ESCV、CV（cross validation）和BIC应用与Lasso方法，并对这三种方法所估计的模型的稳定性进行比较，结果表明ESCV方法在多个指标上面都表现较好。基于此，本文将ESCV作为一种选参方法引入到变系数模型加罚估计中，以期提高变系数模型在传统变量选择方法BIC下的模型稳定性，挑选λ的准则是选择具有局部最小标准化方差的[λ]，即就是要使ES(λ)值最小。

本文的分析比较中，选用模型预测均方误差（MSE）、模型大小（MS）以及显著性变量个数（NOSV）及其百分比（PSV）四个方面来度量模型的稳定性。均方误差是度量模型稳定性的首要标准，模型预测能力不好，则模型不可靠。模型大小即所选变量的个数，在高维数据分析中，需要控制模型复杂度，若所选变量过多，模型太过复杂，模型的稳定性就可能得不到保证。在众多变量中对模型有显著性影响的自变量对模型稳定性有重要影响，显著性变量个数及其百分比是指挑选多个变量的情况下，对模型有显著影响的自变量个数及其占所选全部变量的比例。

3　模拟研究

3．1　正态分布下变系数模型模拟

本文的次模拟是模拟实际中常见的数据分布形式，即自变量服从或近似服从正态分布的情形，模拟所采用的模型如下：

其中假定X=(Xi1,Xi2,Xi3)服从正态分布N(0,1)，ei服从正态分布N(0,0.8)，σe=1.2，并设定不显著变量(Xi4,…,Xip)服从正态分布N(0,0.8)，全部变量之间的协示变量Z服从

i均匀分布U(0,1)。

在自变量来自正态分布的变系数模型中，本文用KLASSO方法进行参数估计和变量选择，在估计过程中，调节参数分别选用ESCV准则和传统的BIC准则进行确定。为了比较在不同变量维度下BIC和ESCV方法进行变量选择对模型稳定性的影响，本文设定总变量数p∈{10,30,60,70,90,100}。

在模型样本量n=50不变，变量数p不断增大的情况下，将每个模型随机模拟100次，结果如表1所示。

表1　正态分布下模拟结果

从表1中可以看出，在样本量n=50保持不变而总变量数p变化时，两种变量选择方法的均方误差（MSE）都随着变量总数的增加而增大。当变量维度p小于样本量n，即当p为10和30时，ESCV方法估计的预测误差、变量个数以及显著性百分比都不如BIC方法，但在高维数据情形下，即当变量维度p大于样本量n时，ESCV方法的预测误差、变量个数以及显著性变量百分比优于BIC方法且这种优势随着变量维度p的增大越发明显。

当样本量n=50，变量维度p=70时，ESCV的100次模拟平均预测误差为2.29，BIC的100次模拟平均预测误差为2.80，ESCV所选模型的MSE小于BIC所选模型且较BIC所选模型的MSE降低了18.21%，同时ESCV的100次模拟所选变量个数平均为16.92，BIC的100次模拟所选变量个数平均为42.88，ESCV所选模型的变量个数不到BIC所选模型变量个数的一半，ESCV方法较BIC大大缩减了模型变量维度，在显著性变量占所选变量百分比上，ESCV所选模型的显著性变量百分比为14.36%，是BIC所选模型的两倍。当p=100时，ESCV所选模型的MSE较BIC所选模型降低约20%，ESCV所挑选的变量个数仅占全部变量数的16.05%，而BIC所选变量个数占全部变量数的66.29%，ESCV所选变量个数大约是BIC所选变量个数的四分之一，在显著性变量百分比上，ESCV所选模型的显著性变量百分比为14.70%，是BIC所选模型的三倍。由上述分析可知，当变量维度p大于样本量n时，ESCV方法在模型稳定性上的表现优于BIC，且在样本量不变的情况下，随着变量维度p的增加优势越发明显。

3．2　稀疏情况下变系数模型模拟

Lim和Yu（2013）[5]给出在高维稀疏情况下，ESCV方法较BIC估计方法更能突显模型的稳定性优势，因此，改变变系数模型中自变量的分布，将自变量分布稀疏化来探讨在自变量稀疏情况下，ESCV方法与传统变量选择方法BIC在模型稳定性上的不同表现。

模拟模型假定与第一种情况相同，只是假定自变量X来自于服从均匀分布的随机稀疏矩阵sprand(ss,p,d),其中ss为样本量，p为总变量个数，d为非零元素分布密度的大小，设为0.4。

模型在样本量n=50保持不变，总变量数p∈{10,30,60,70,90,100}的情况下，对每组模型设定都进行100次模拟，在KLASSO估计方法下，分别选用ESCV选参准则和BIC选参准则来选择调节参数，结果如表2所示。

表2　稀疏情况下模拟结果

从表2可以看出，自变量来自于稀疏分布情形时，在样本量p小于n的情况下，即p=10或30时，在均方误差MSE上，ESCV方法所选模型对应的均方误差较BIC方法要小，在模型大小以及显著性变量百分比上，ESCV方法对应的模型较BIC要大，但随着变量维度的增加，当变量维度p大于样本量n，即p∈{60,70,90,100}时，ESCV筛选变量的优势大大增强，均方误差也越来越小。当p=100时，ESCV方法平均100次模拟的均方误差为1.06，BIC方法对应的均方误差为1.18，ESCV方法的对应模型的MSE较BIC减少了10.17%，且ESCV方法为模型所挑选的变量个数平均为4.09，大大少于BIC方法所选变量个数33.77，ESCV所选变量个数大约是BIC方法所选变量个数的四分之一，在显著性变量百分比上，ESCV所选显著性变量占全部所选变量的50.86%，而BIC方法所选显著性变量占所选全部变量的7.26%，即BIC方法较ESCV方法更多的选择了不显著变量。

与自变量来自于正态分布下的变系数模型相比，稀疏分布下两种方法拟合的模型在模型均方误差、模型大小、显著性变量百分比上的表现都更好，但与BIC方法相比，ESCV方法对模型稳定性的影响更为显著，即ESCV方法下的模型均方误差、模型大小减小幅度更大，显著性变量百分比增大幅度则更多，如稀疏情形下，BIC方法对应的模型大小是正态分布下模型大小的二分之一，而ESCV方法对应的模型大小是正态分布下的四分之一。且稀疏分布情形下，低维时，ESCV方法对应的模型均方误差小于BIC，这与自变量来自于正态分布且数据为低维情况下ESCV预测误差大于BIC相反。高维时，不论自变量来自哪种分布，ESCV在均方误差、模型大小、显著性变量百分比上都优于BIC。在高维稀疏数据分析中，ESCV较BIC方法的稳定性优势更加明显。

4　实例分析

4．1　Boston Housing数据分析

本文将分析Boston住房数据，该数据是在1970年Boston地区收集的506个人口普查区的房价信息。本文沿用Fan和Huang（2005）[9]的变量设定，将MEDV（业主自用房子的中位数，以$1000为单位）作为响应变量Y，LSTAT（地区较低地位人群占总体的百分比）作为指示变量Z，数据集中的其他七个变量作为自变量INT（截距，X1），CRIM（镇上人均犯罪率，X2），RM（每座房子的平均房间数，X3），PTRATIO（镇上学生-老师人数比，X4），NOX（氮氧化物浓度，X5），TAX（房间全价值物业税率，以$10000为单位，X6）和AGE（业主占用房子建造早于1940年的比例，X7）。

将全部506个样本单元随机分成十份，每次选取其中九份做训练集，另一份为预测集。在应用模型之前，需要将自变量X和指示变量LSTAT标准化处理。由抽取的训练集数据建立变系数模型，并在KLASSO方法下分别选用ESCV与BIC两种方法进行变量选择，记录10次抽样数据拟合中每个变量被选入模型的次数，以及每次模型预测集的均方误差MSE，结果如表3所示。

从表3中可以看出，对10次拟合进行平均，ESCV的均方误差MSE与BIC方法对应模型的MSE相当，但在10次拟合中，ESCV方法倾向于选择前三个变量，变量X1，X2，X3被选中的次数分别为10、9、10，即ESCV方法能够稳定的选择出前三个自变量，而BIC方法在每次模拟时所选变量的个数以及倾向于选择哪些变量都不稳定，即抽样数据不同时，BIC不能保证所估计模型的稳定性。

为了进一步理解抽样数据分析中的不稳定性，给出第6次抽样下，BIC方法对应模型的估计系数图，如图1（上）；ESCV方法所对应模型的估计系数图，如图1（下）。

从图1（上）中可以看出，在BIC方法下，用此次抽样所得的455个数据进行变量选择，所选取的变量数为1，即仅第一个变量INT显著不为0，其他六个变量的全部估计为0。用此次数据建立模型并对余下的51个数据进行预测，所对应的平均预测误差为0.5115；图1（下）给出了相同样本数据下，用ESCV方法进行变量选择，所选取的变量个数为3，即INT、RM、CRIM这3个变量显著不为0，用所建模型对余下的51个数据进行预测，所对应的平均预测误差为0.4082。对比两个图可以看出在一次抽样数据拟合中，对同一个自变量的估计，例如自变量INT，ESCV方法对该变量估计的波动程度要显著小于BIC方法，即ESCV方法估计的变量系数更为稳定。

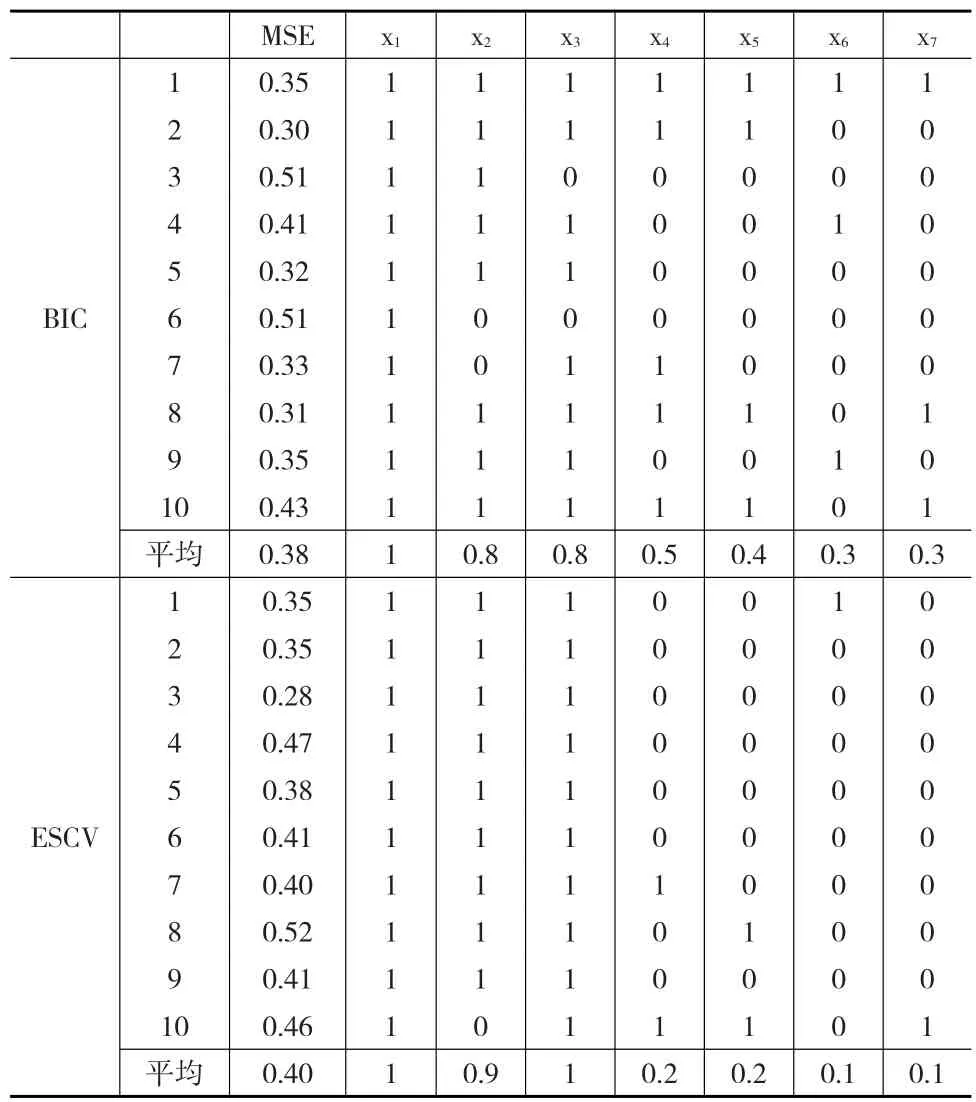
表3　Boston住房数据结果

图1 BIC（上）和ESCV（下）方法下自变量估计系数变动情况

从Boston housing的数据分析中可以看到，当所抽取的样本数据发生变化时，BIC方法选择的变量个数就会随之发生大的变动，而ESCV却能稳定地选出对因变量有重要影响的自变量，且对所选变量的系数估计也更稳定。

4．2　新浪新闻数据分析

利用爬虫技术在新浪新闻网站获取2013年7月1日至9月30日（共12周）财经（标签为+1）和健康（标签为-1）两类新闻文档。共390篇，两类的比例为1：1。利用分词软件将原始文本数据转化为文档词频矩阵。随机选取150篇文档为训练集，剩余240篇为测试集。利用LASSO初步筛选出162个关键词。指示变量z为时间并以周为时间单位。即假定关键词对新闻类别的影响与其出现的时间有关。

在变系数模型KLASSO估计中，分别用ESCV和BIC两种方法确定调节参数，用所确定模型的分类准确率来衡量模型预测误差，用所选择变量的个数来确定模型大小。将数据进行10次抽样，并对每次抽样所得数据进行拟合，每次拟合模型所选变量数，以及模型分类准确率所得结果如表4所示：

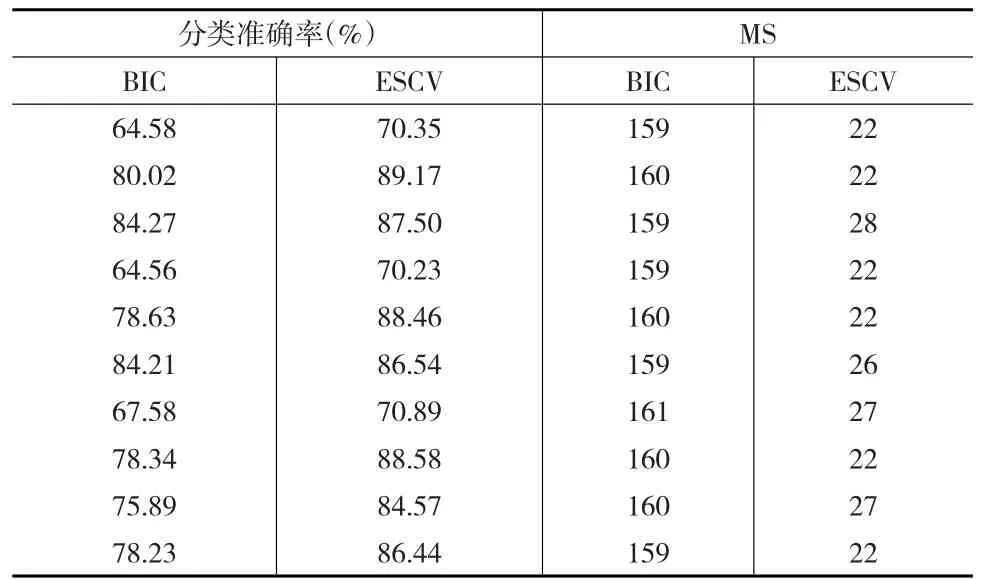
表4　新闻数据分类准确率和模型大小

从表4中可以看出，在样本量n=150小于变量维度p=162时，尽管10次所抽取的样本数据不一样，但用ESCV方法选择出的变量所建模型的分类准确率始终要大于BIC方法的分类准确率，且在模型大小上，BIC方法倾向于选择几乎所有的变量，而ESCV倾向于选择固定的20多个变量，ESCV挑选出的变量个数始终显著小于BIC方法下的变量个数，在此次新闻数据分析中，ESCV变量选择方法有明显的降维作用，在分类准确率上较传统BIC方法也有优势，采用ESCV变量选择方法可以显著提高模型的稳定性。

为了更好地理解ESCV选择变量的稳定性要优于BIC，给出某次抽样下，ESCV选择变量的情况，如在第四次抽样中，ESCV在162个关键词中，选择了22个对分类有重要影响的关键词，即选择的变量个数为22。分析这22个关键词，大致可以分为三大类，第一类是明显跟经济类相关的词，如：美元、经济、投资、下降、涨、中国、企业、发展、部门；第二类是跟健康类相关词，如：医院、性、肌肉、成分、疾病、健康、破坏、食物、效果；第三类是对分类没有很重要作用，但在两类文章中都会出现的词，如：发布、公布、好。

在此次抽样中，BIC方法所选变量个数为160，几乎所有由LASSO初步筛选出的关键词都被引入到模型中。因此BIC所建模型比ESCV更复杂。在两种选参方法下，“健康”一词都被选中，但两种方法对其重要性的估计不同，下面本文给出两种方法下，关键词“健康”在12周中估计系数的变化对比图，如图2所示。

图2ESCV和BIC方法下关键词“健康”估计系数变化图

从图2中可以看出，在12周中，“健康”一词在分类上始终是有重要作用的词汇，但在BIC方法下估计出的系数值即关键词重要性波动较大，而在ESCV方法下估计系数值变动较小，在前4周几乎没有变动，第4周略有下降，但在后4周中又开始固定不变，系数值基本保持在0.4995的水平上，ESCV比BIC方法对该词的估计更为稳定。

从新浪新闻数据分析可以看出，在高维数据情况下，ESCV在模型预测、变量选择上较BIC表现得更好，即在变系数模型KLASSO估计下，选用ESCV准则比选用BIC准则进行变量选择所确立模型的稳定性更强。

5　总结

本文是基于Yu和Lim（2013）[5]提出的ESCV方法以及对模型稳定性的度量标准，将ESCV方法引入到变系数模型加罚估计中，以期提高变系数模型的稳定性。本次研究主要是基于Wang和Xia（2009）[4]提出的变系数模型KLASSO估计，在KLASSO估计实际计算中，分别应用ESCV方法与BIC方法进行调节参数的选择，并对比不同选参方法对模型稳定性的影响，而模型稳定性主要从模型预测误差、模型大小和显著性变量百分比上来进行比较。

本文虽然找到了一种能够提高变系数模型稳定性的方法，但同样存在很多问题：首先对于模型稳定性统计学上还没有给出标准的定义，本文只能直观地从预测误差、选择变量等方面来衡量模型是否稳定；其次变系数模型有很多估计方法，而此次研究仅限于KLASSO估计，在其他变系数模型估计方法下，ESCV方法是否能够比BIC方法表现好还有待进一步研究；最后数据在低维情形时，多次抽样情况下，虽然ESCV方法的变量选择稳定性要优于BIC，但是BIC方法的平均预测误差要小于ESCV，ESCV方法可能存在总是漏选某个重要变量的情况。

参考文献：

[1]Hastie T,Tibshirani R.Varying Coefficient Models[J].Journal of Royal Statistical Society:Series B,1993,(55).

[2]Fan J,Zhang W.Statistical Estimation in Varying Coefficient Models[J].Journal of the American Statistical Association,1999,(27).

[3]Chiang C,Rice J A,Wu C O.Smoothing Spline Estimation for Varying Coefficient Models With Repeatedly Measured Dependent Variables[J].Journal of American Statistical Association,2001,(96).

[4]Wang H,Xia Y.Shrinkage Estimation of the Varying Coefficient Model[J].Journal of the American Statistical Association,2009,(104).

[5]Lim C,Yu B.Estimation Stability With Cross Validation(ESCV)[J].arXiv,2013,(1303).

[6]Yuan M,Lin Y.Model Selection and Estimation in Regression With Grouped Variables[J].Journal of the Royal Statistical Society:Series B,2006,(68).

[7]Yu B.Stability[J].Bernoulli,2013,19(4).

[8]Breiman L.Heuristics of Instability and Stabilization in Model Selection[J].Annals of Statistics,1996,(24).

[9]Fan J,Huang T.Profile Likelihood Inferences on Semiparametric Varying Coefficient Partially Linear Models[J].Bernoulli,2005,(11).