面板数据复合分位数回归模型的估计

徐洁，杨宜平

（重庆工商大学数学与统计学院，重庆400067）

0　引言

目前，在计量经济学、社会学、生物医学等领域经常遇到面板数据，对该类数据的研究也取得了一系列的进展。武大勇[1]介绍了个体固定效应模型中基于最小二乘法参数的估计问题。申敏等[2]基于面板数据对我国省级行政区企业技术创新产出弹性结构进行分析。杨慧敏[3]采用混合最小二乘法对公司的股权结构、治理以及绩效进行回归分析等。

上述研究在建立面板数据模型分析时，均采用最小二乘回归法估计模型中的参数。最小二乘法局限性较大，外部条件较为严格，如回归模型中模型误差项满足方差相同、服从正态分布等。最小二乘估计稳健性也较差，当数据中存在异常点时，最小二乘估计可能会表现得很糟糕。Koenker和Bassett[4]提出的分位数回归方法成为了最小二乘估计的有力补充和推广。已有一些学者将面板数据和分位数回归结合对变量之间的关系进行分析。李群峰[5]以固定效应面板模型为例，通过迭代求解估计了不同分位数回归方程的参数并对最小二乘法同分位数回归法做比较分析，发现后者不仅能测度自变量对因变量在某个特定分位数下的边际效果，还能提高参数的显著性。

分位数回归提供了不同分位点处的估计结果，对模型假定较少且具有稳健性等优良统计性质，但其回归系数总随着分位数的变化而变化。能否将多个分位数回归模型的信息综合起来，得到回归系数一个更有效的估计呢？Zou和Yuan[6]提出了复合分位数回归方法，它综合了多个分位数处的分位数回归得出回归系数更有效的估计。该方法既保留了分位数回归的稳健性，又通过复合的方式改进了估计的效果，可以成为最小二乘估计的可靠替代。然而到目前为止还没有文献讨论面板数据的复合分位数回归，因此促使本文考虑面板数据复合分位数回归模型。

本文考虑个体固定效应面板数据模型，为了避免参数祸根问题，引入一个幂等矩阵消除个体效应项。然后采用Zou和Yuan[6]提出的复合分位数回归方法估计回归系数，并证明了其渐近性质。

1　回归系数估计

考虑如下面板数据个体效应模型：

其中xit=(xit,1,xit,2,...,xit,p)T是p维外生解释变量,Yit是响应变量,αi是不可测量的个体效应,uit是相互独立的模型误差。在固定效应模型中,要求个体效应{αi}与解释变量{xit}是相关的，并且具有未知的相关结构。为了模型的可识别性，假定

由于面板数据观测个体比较多，数据容量较大。观测个体的增多会引起估计参数αi的增多，这样则会引起参数祸根问题。为了避免参数αi的估计，本文引入一个幂等矩阵来消除个体效应项αi。

为了简单起见，令Yi=(Yi1,Yi2,...,YiT)T是T×1向量，xi=(xi1,xi2,...,xiT)T是T×P矩阵，ui=(ui1,ui2,...,uiT)T是T×1向量，eT是所有元素为1的T×1向量，则模型（1）可表示为矩阵形式：

令Q为一个T×T幂等矩阵且满足QeT=0，在模型（2）中两边乘以Q得：

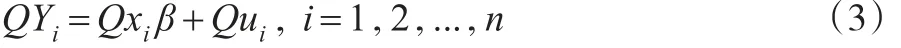
显然，QeT=0有效地消除了未知的个体固体效应αi。

满足条件的矩阵Q并不唯一，在这里取：Q=IT-

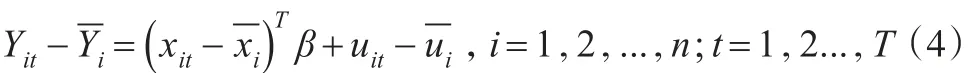
对模型（4），采用Zou和Yuan[6]提出的复合分位数方法构造回归系数β的估计。

2　渐近性质

（C2）xit具有有界支撑；

（C3）密度函数f(⋅)有大于零的下界，一阶导函数连续且一致有界。

定理1：如果条件C1至C3成立β0,aτk0是参数真值，则有：

证明：记β0，aτk0是参数真值，令下式的最小化解。

其中

根据Knight[7]中等式（2-13）：

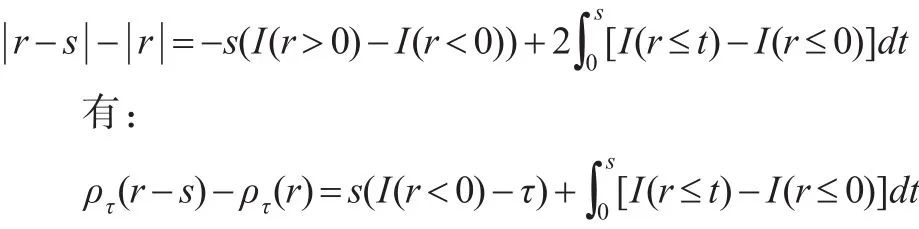
因此，Ln可以表示为：

因此：

由于Ln是凸函数，有：

同时：

那么，由中心极限定理可得定理1。

3　结束语

本文考虑面板数据回归模型，提出了回归系数的复合分位数估计。在构造估计量时，为了避免估计个体效应项所带来的维数祸根问题，通过对面板数据回归模型乘一个幂等矩阵消去固定效应部分。在一些正则条件下，证明了所提出的估计量渐近于正态分布。本文提出的复合分位数估计，不仅保留了分位数回归的优点，而且还综合了多个分位点的信息。

参考文献：

[1]武大勇.计量经济学中的面板数据模型分析[D].武汉：华中科技大学硕士论文,2006.

[2]申敏,吴和成,华海岭.技术创新产出弹性结构分析——基于面板数据聚类分析和偏最小二乘回归[J].技术经济,2014（,1）.

[3]杨慧敏.股权结构、公司治理与公司绩效[D].天津：天津大学硕士论文,2007.

[4]Koenker R,Bassett G W.Regression Quantiles[J].Econometrica,1978（,46）.

[5]李群峰.基于分位数回归的面板数据模型估计方法[J].统计与决策,2011（,17）.

[6]Zou H,Yuan M.Composite Quantile Regression and the Oracle Model Selection Theory[J].The Annals of Statistics，2008.

[7]Knight K.Limiting Distributions forl1Regression Estimators Under General Conditions[J].The Annals of Statistics,1998（,26）.