低频流动性指标优劣评估——基于中国股票市场的实证分析

，　，　

(1.浙江财经大学 金融学院，浙江 杭州 310018； 2.上海交通大学 安泰经济与管理学院,上海 200030)

1　引言

流动性危机的频频发生表明流动性问题是一种非常重要的市场摩擦。流动性是一个复杂的、多维度的概念，通常是指一种能够以较低成本迅速成交大量证券并对价格产生较小影响的能力[1,2]。 “较低成本”、“大量证券”、“迅速成交”和“较小影响”反映了流动性的四个维度，分别是宽度、深度、即时性和价格冲击。宽度是指交易价格偏离市场中间价格的程度，即不考虑市场价格时的总成本；深度是在不影响市场价格的前提下可以完成的最大交易量；即时性主要指证券成交的速度；价格冲击是指单位交易引起的价格变化幅度。然而，流动性本身无法直接观测。现有文献中提出了许多衡量流动性的指标，这些指标从不同维度、不同侧面反映流动性某些方面的特征，但无法反映流动性的全貌。国内外已有一些学者对流动性指标进行了梳理，如Amihud等[3]，杨朝军[4]，Chai等[5]，尹海员和李忠民[6]，张玉龙和李怡宗[7]。但是这些文献中讨论的流动性指标大多数是早期研究提出的。近20年来，流动性指标的研究取得了非常大的进展，新提出和改进的流动性指标却很少得到关注和应用。

纷繁众多、质量参差不齐的低频流动性指标，一方面给研究者带来一定的困扰，另一方面使用不同的指标常常会得到不一致甚至相矛盾的结论[8,9]。因此，一个好的流动性指标对实证研究至关重要[5]。Goyenko等[8]对美国股票市场流动性低频指标的优劣进行了评估。类似地，张峥等[10]，陈辉[11]对中国股票的流动性低频指标的优劣进行了检验。但是这两篇文献存在着不足：一方面，他们仅仅采用了宽度维度的基准指标；另一方面，他们所检验的流动性间接指标不多，且主要是早期文献提出的，较少涉及近期文献。因此，本文拟以宽度、深度和价格冲击三个维度的指标为基准指标，根据横截面相关系数、时间序列相关系数和预测误差三个评估标准，对近20年文献中常用的流动性低频指标进行评估，旨在为今后流动性的研究者们提供一个参考。

2　流动性指标的计算方法

文献中常见的流动性指标是宽度、深度和价格冲击维度的指标。即时性维度的指标很少，也并未得到广泛的使用。因为计算需要实际委托时间的数据很难获得，而且即时性与价格和订单规模大小密切相关。在任何一个市场，如果投资者愿意接受极为不利的价格或者订单规模很小，交易一般均能够得到迅速执行。因此，本文主要评估的是宽度、深度和价格冲击三个维度的流动性低频指标。根据计算方法的不同，流动性指标可以分为高频指标和低频指标。高频指标，又称直接指标，是由日内高频数据计算。低频指标，又称间接指标，基于市场微观结构理论使用低频数据计算[10]。由于低频数据在即时性和可得性方面远远优于高频数据，低频指标在金融市场和研究中得到广泛的应用，但是低频指标在准确性和适用性方面需要注意。

2.1　基准指标

(1)宽度维度的基准指标：有效价差(ES)和实现价差(RS)，根据Goyenko等[8]，公式如下

ES=2×|lnPk-lnMk|

(1)

RS=2×|lnPk-lnMk+5|

(2)

其中Pk为第k笔订单的成交价格，Mk为第k笔订单到达时的中间价，Mk+5为第k笔订单成交5分钟后的中间价。

(2)深度维度的基准指标：市场深度[12]

(3)

(3)价格冲击维度的基准指标：根据Goyenko等[8]

rn=λ×Sn+μn

(4)

2.2　低频指标

(1)宽度维度的低频指标

Roll[13]根据价格一阶差分序列的协方差估计有效价差

(5)

其中cov是协方差函数,ΔPd=Pd-Pd-1,Pd是第d个交易日的收盘价。

Roll指标只适用于价格变化序列负相关的资产，Goyenko等[8]对Roll指标进行了如下改进

(6)

Kim和Lee[14]对Roll指标也进行了改进

(7)

根据Lesmond等[15]，Zeros指标计算公式为

Zeros1=n1/N,Zeros2=n2/N

(8)

其中n1是考察期内(例如一个月)收益率为零的交易天数，n2是考察期内交易量为正且收益率为零的交易天数，N是考察期内总的交易天数。

Kang和Zhang[16]认为交易量为零的天数越多意味着流动性越低

ZerosVol=n3/N

(9)

其中n3是考察期内交易量为零的交易天数。

若许多股票在考察期交易量为零的交易天数相同，根据ZerosVol指标这些股票的流动性水平相同，为避免这种情况，Liu[2]对ZerosVol指标进行了改进

(10)

Corwin和Schultz[17]根据方差与收益率的时间间隔成比例，而价差与收益率的时间间隔无关这一事实，将波动成分从价格比率中剥离，基于最高价与最低价之比构造了一个价差指标

(11)

Lesmond等[15]提出

LOTMixed=α1j-α2j

(12)

其中α1j是卖出股票j的交易成本，α2j是买入股票j的交易成本，并且满足以下极大似然估计

L(α1j,α2j,βj,σj|Rj,d,Rm,d)

s.t.α1j≤0,α2j≥0,βj≥0,σj≥0

(13)

其中φ(·)是标准正态密度函数，Φ(·)是标准正态分布函数。以上估计有三个域，域0是Rj,d=0，域1是Rj,d≠0且Rm,d>0，域2是Rj,d≠0且Rm,d<0。Rj,d是股票j第d个交易日可观测的收益率，Rm,d是市场第d个交易日的收益率。βj是股票j对市场的敏感度，σj是股票j收益率的波动率。

Goyenko等[8]在不同的域上估计极大似然方程(13)，域0是Rj,d=0，域1是Rj,d>0，域2是Rj,d<0，得到LOTYsplit指标。除了估计的域不同，LOTYsplit与LOTMixed表达式完全一样。

Fong等[18]对LOT模型进行简化，得到指标

(14)

(2)深度维度的低频指标是交易量(Volume)和换手率(Turnover)[19]。

(3)价格冲击维度的低频指标

Pástor和Stambaugh[1]根据以下等式构造了一个衡量股票流动性的价格冲击指标

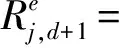
Voldj,d+εj,d+1d=1,…,N

(15)

Amivest流动性比率由Amivest资产管理公司提出并得到广泛使用[20]，衡量导致价格变化一个百分点所需要的交易量，计算公式为

(16)

其中Tj是股票j某个月交易量不为零的交易天数；|Rj,d|是股票j第d个交易日的收益率绝对值。

Amihud[21]以单位交易引起价格变化百分比衡量流动性

(17)

杨朝军[4]指出Amihud指标的收益率是包含非交易时间，考虑到信息一般是在非交易时间公布，为排除价格变化是由于新信息出现导致的影响，他采用交易时间段内的价格变化对Amihud指标进行改进

(18)

Florackis等[22]指出Amihud指标存在规模偏差，且忽视股票的持有期限。他们以换手率代替交易金额对Amihud指标进行改进

(19)

Kang和Zhang[16]指出在欧美等成熟的股票市场上，股票交易频繁，出现股票交易量为零的情况的概率非常低，但是在新兴股票市场上，出现股票交易量为零的情况的概率很高。他们对Amihud指标进行如下改进

(20)

Goyenko等[8]提出扩展的Amihud指标

(21)

其中Spread是宽度指标。本文据此构造了Roll_impact、RollGHT_impact、RollKL_impact、Zeros1_impact、Zeros2_impact、ZerosVol_impact、ZerosLM_impact、HLPrice_impact、LOTMixed_impact、LOTYsplit_impact和LOTFHT_impact。

3　实证分析

3.1　数据与方法

本文采用2006年1月到2015年12月的股票交易高频数据和日度数据，前者来源于港澳资讯金融数据库，后者来源于国泰安中国股票市场交易数据库。参考张峥等[10]，本文剔除特别处理的股票(即ST股)，删除股票IPO当月的交易数据，剔除开盘(上午9∶30)前或收盘(下午3∶00)后的交易记录。结合第2节流动性指标的计算方法，对2006～2015年期间的股票交易日度数据做简要分析发现：(1)股票在正常交易状态下交易量为零的情况几乎为零，对所有样本股票有：ZerosVol=0，Zeros1=Zeros2，ZerosLM与Zeros1、AmihudKZ与Amihud无本质区别，因此在以下研究中，我们没有考察Zeros2、ZerosVol、ZerosLM和AmihudKZ指标，以及Zeros2_impact、ZerosVol_impact和ZerosLM_impact。(2)股票收益率为零的情况不多，约占样本观察的33%，对67%的样本观察有：Zeros1=0；LOTFHT=0，表明Zeros1和LOTFHT指标不能够很好地衡量我国股票的流动性状况。为了减少异常值的影响，本文对所有流动性指标做5%的Winsorize处理。

根据Goyenko等[8],Fong等[18]，本文采取以下三种方法对流动性指标进行评估：(1)横截面相关系数，反映同一时间点上流动性指标之间的相关性。(2)时间序列相关系数，反映流动性指标长期的相关性。(3)预测误差，是流动性低频指标与相应基准指标的偏差，以均方根误差(Root Mean Squared Error, RMSE)来衡量，由于各指标的量纲不同，本文对各指标进行标准化处理后再计算均方根误差。

3.2　横截面相关系数

本文分别以宽度维度的有效价差和实现价差、深度维度的市场深度以及价格冲击维度的λ为基准指标，计算相同维度的低频指标与基准指标的横截面相关系数。如果低频指标能够很好地捕捉相应维度的基准指标，那么其与基准指标的相关系数应该越高。具体地，每个月计算低频指标与基准指标的横截面相关系数，然后计算横截面相关系数的时间序列均值，结果如表1所示。

首先，在宽度维度的8个低频指标与基准指标的横截面相关系数中，LOTYsplit指标与基准指标(ES和RS)的横截面相关系数最高，分别为0.227和0.265，显著地优于其他低频指标，表明LOTYsplit能很好地捕捉流动性宽度维度的概念。Fong等[18]的研究显示在1996～2007年期间，中国股票市场上LOTMixed指标与基准指标(有效价差)的横截面相关系数最高。其次，在深度维度的2个低频指标与基准指标的横截面相关系数中，Volume指标与基准指标(D)的横截面相关系数最高，为0.413，表明交易量指标比换手率指标能更好地捕捉流动性深度维度的概念。最后，在价格冲击维度的13个低频指标与基准指标的横截面相关系数中，AmihudYCJ指标与基准指标(λ)的横截面相关系数最高，为0.806，显著地优于其他低频指标，表明AmihudYCJ指标能很好地捕捉流动性价格冲击维度的概念。Fong等[18]的研究显示在1996～2007年期间，中国股票市场上Amihud指标与基准指标(λ)的横截面相关系数最高。张峥等[10]也发现在1999～2009年期间，Amihud指标与基准指标(相对价差和有效价差)的横截面相关系数最高。但是这两个文献均没有考察AmihudYCJ指标。横截面相关系数结果表明，宽度维度中的低频指标LOTYsplit指标最优，深度维度中的低频指标Volume指标最优，价格冲击维度的低频指标AmihudYCJ指标最优。

表1　流动性低频指标与基准指标的横截面相关系数

3.3　时间序列相关系数

横截面相关系数反映了同一时点上流动性指标之间的相关关系。时间序列相关系数则反映流动性指标之间长期的相关关系。具体地，将所有样本股看成一个投资组合，计算组合内股票各流动性指标的等权重均值，得到组合各流动性指标的时间序列，比较组合的流动性低频指标与基准指标的时间序列相关系数。结果如表2所示。

首先，在宽度维度的8个低频指标与基准指标的时间序列相关系数中，RollKL指标与基准指标(ES和RS)的时间序列相关系数最高，分别为0.640和0.657。根据Fisher的Z检验，Roll和HLPrice指标与基准指标的时间序列相关系数在5%的显著性水平下同RollKL与基准指标的时间序列相关系数没有差异，表明从长期来看RollKL、Roll和HLPrice指标能很好地捕捉流动性宽度维度的概念。其次，在深度维度的2个低频指标与基准指标的时间序列相关系数中，Volume指标与基准指标(D)的时间序列相关系数最高，为0.467，表明从长期来看交易量指标比换手率指标能更好地捕捉流动性深度维度的概念。最后，在价格冲击维度的13个低频指标与基准指标的时间序列相关系数中，Amihud指标与基准指标(λ)的时间序列相关系数最高，为0.892。AmihudYCJ指标与基准指标(λ)的时间序列相关系数为0.882，根据Fisher的Z检验，在5%显著性水平下同Amihud指标与基准指标的时间序列相关系数没有差异，说明从长期来看，Amihud和AmihudYCJ指标能很好地捕捉流动性价格冲击维度的概念。时间序列相关系数结果表明，宽度维度中的低频指标RollKL指标最优，Roll和HLPrice指标与RollKL没有显著差异；深度维度中的低频指标Volume指标最优；价格冲击维度中的低频指标Amihud指标最优，AmihudYCJ指标与Amihud指标没有显著差异。

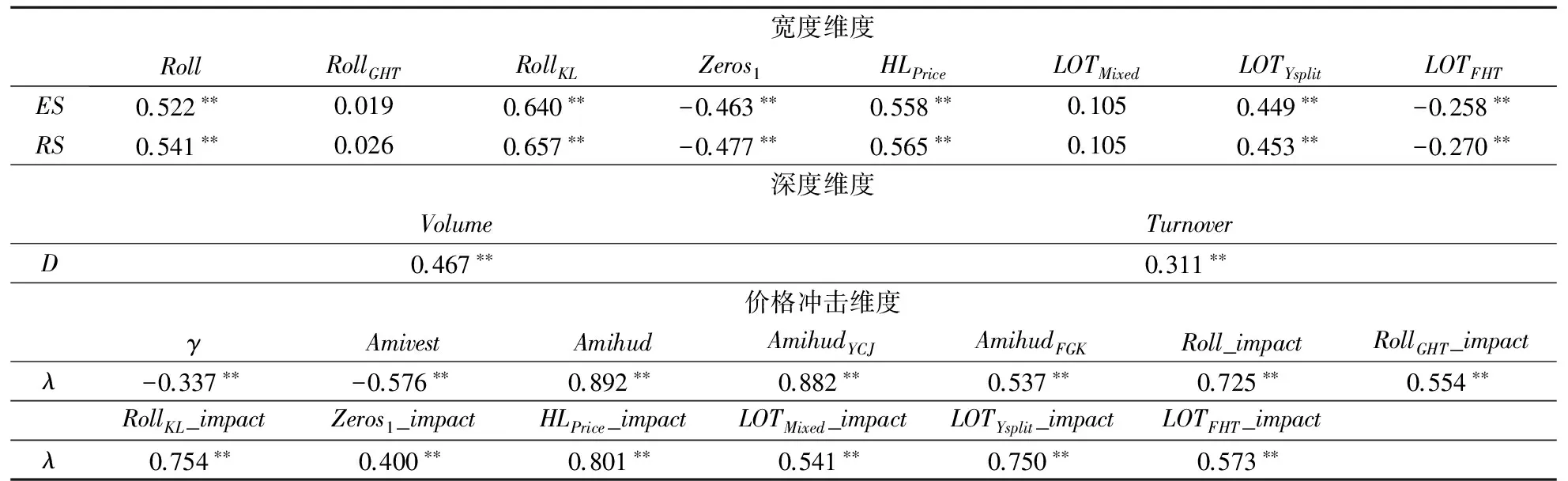
表2　流动性低频指标与基准指标的时间序列相关系数

3.4　预测误差

横截面相关系数和时间序列相关系数评价标准不关注低频指标实际大小，侧重其与基准指标相关程度的高低。预测误差评估标准关注低频指标实际大小，侧重其刻画基准指标的精确程度，通常用均方根误差来衡量。由于流动性指标的量纲不完全相同，本文首先将所有股票的流动性指标进行标准化处理，然后计算每个月标准化的低频指标与基准指标的均方根误差，最后求均方根误差的时间序列均值。结果如表3所示。

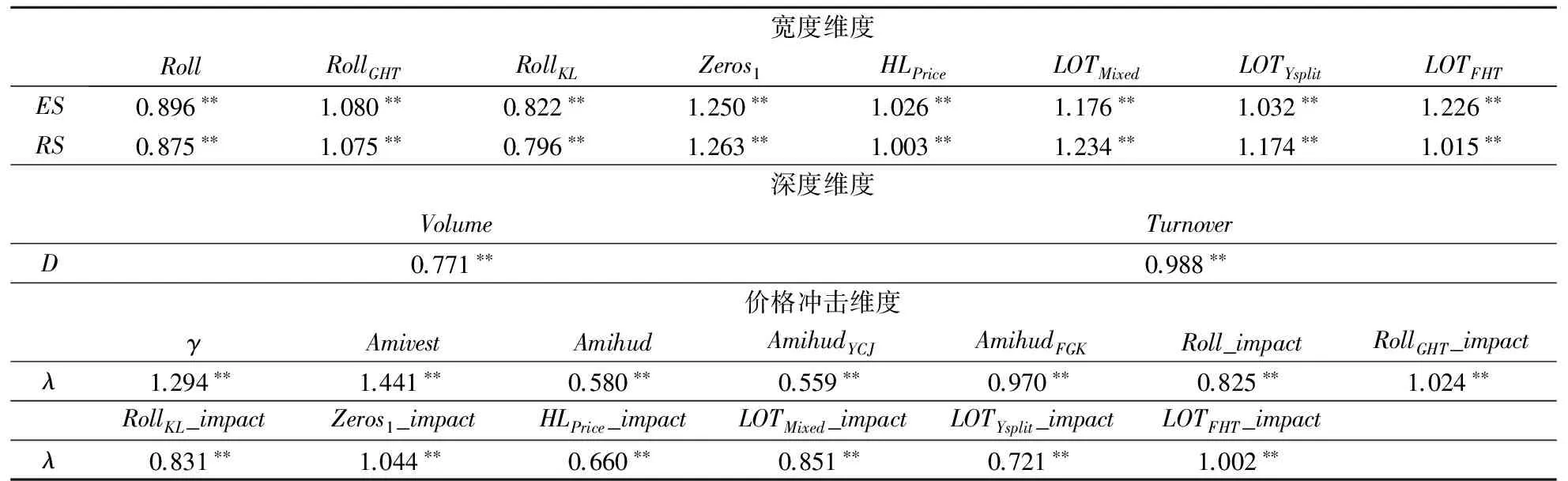
表3　流动性低频指标与基准指标的均方根误差

注：由于单位不同，将所有股票的上述流动性指标进行标准化处理后再计算均方根误差。

首先，在宽度维度的8个低频指标与基准指标的均方根误差中，RollKL指标与基准指标(ES和RS)的均方根误差最小，分别为0.822和0.796，表明RollKL指标能够最准确地刻画有效价差和实现价差。其次，在深度维度的2个低频指标与基准指标的均方根误差中，Volume指标与基准指标(D)的均方根误差最小，为0.771，表明Volume指标比Turnover指标能更准确地刻画市场深度。最后，在价格冲击维度的13个低频指标与基准指标的均方根误差中，AmihudYCJ指标与基准指标(λ)的均方根误差最低，为0.559。Amihud指标与基准指标(λ)的均方根误差为0.580，根据双样本t检验，在5%显著性水平下同AmihudYCJ指标与基准指标的均方根误差没有差异，说明AmihudYCJ和Amihud指标能很好刻画价格冲击。均方根误差结果表明，宽度维度中的低频指标RollKL指标最优；深度维度中的低频指标Volume指标最优；价格冲击维度中的低频指标AmihudYCJ指标最优，Amihud指标也很好。

4　结论与启示

金融市场在近几十年频频发生流动性危机，使得流动性成为一个非常重要的课题，受到了投资者、监管者和研究者的高度重视和广泛关注。国内外有大量关于流动性的研究。由于流动性是一个复杂的、多方面的概念，而且无法直接观测，导致现有文献中流动性指标纷繁众多、质量参差不齐，给研究者带来很大的困扰。因此，一个好的流动性指标对实证研究至关重要。本文应用2006～2015年中国股票高频交易数据计算流动性的宽度、深度和价格冲击三个维度的指标作为基准指标，以横截面相关系数、时间序列相关系数和预测误差为评估标准，对近20年文献中提出和改进的流动性低频指标进行评估。总体来看，在中国股票市场中，宽度维度中的低频指标RollKL[14]指标最优；深度维度中交易量比换手率更能够衡量流动性；价格冲击维度中的低频指标AmihudYCJ[4]指标最优。与Fong等[18],张峥等[10]的发现一致，本文实证结果也显示，在中国股票市场上，Amihud[21]指标是一个很好的低频指标。本文的研究为中国股票市场的流动性研究提供了基础，为今后流动性的研究者们提供了一个参考。

参考文献：

[1] Pástor L’, Stambaugh R F. Liquidity risk and expected stock returns[J]. Journal of Political Economy, 2003, 111(3): 642- 685.

[2] Liu W. A liquidity-augmented capital asset pricing model[J]. Journal of Financial Economics, 2006, 82(3): 631- 671.

[3] Amihud Y, Mendelson H, Pedersen L H. Liquidity and asset prices[M]. Hanover: Now Publishers Inc, 2006.

[4] 杨朝军.证券市场流动性理论与中国实证研究[M].上海:上海交通大学出版社,2008.

[5] Chai D, Faff R, Gharghori P. New evidence on the relation between stock liquidity and measures of trading activity[J]. International Review of Financial Analysis, 2010, 19(3): 181-192.

[6] 尹海员,李忠民.流动性衡量及对资产定价的影响研究述评[J].经济与管理研究,2011,(8):65-72.

[7] 张玉龙,李怡宗.资产定价中的市场流动性——流动性文献综述[J].投资研究,2013,(10):3-17.

[8] Goyenko R Y, Holden C W, Trzcinka C A. Do liquidity measures measure liquidity[J]. Journal of Financial Economics, 2009, 92(2): 153-181.

[9] 谢赤,张太原,曾志坚.中国股票市场存在流动性溢价吗?——股票市场流动性对预期收益率影响的实证研究[J].管理世界,2007,(11):36- 47.

[10] 张峥,李怡宗,张玉龙,等.中国股市流动性间接指标的检验——基于买卖价差的实证分析[J].经济学(季刊),2014,13(4):233-262.

[11] 陈辉.日间数据计算买卖价差的两种方法之比较与应用[J].金融评论,2014,6(3):80-90.

[12] Goldstein M A, Kavajecz K A. Eighths, sixteenths and market depth: changes in tick size and liquidity provision on the NYSE[J]. Journal of Financial Economics, 2000, 56(1): 125-149.

[13] Roll R. A simple implicit measure of the effective bid-ask spread in an efficient market[J]. Journal of Finance, 1984, 39(4): 1127-1139.

[14] Kim S H, Lee K H. Pricing of liquidity risks: evidence from multiple liquidity measures[J]. Journal of Empirical Finance, 2014, 25(2): 112-133.

[15] Lesmond D A, Ogden J P, Trzcinka C A. A new estimate of transaction costs[J]. Review of Financial Studies, 1999, 12(5): 1113-1141.

[16] Kang W, Zhang H. Measuring liquidity in emerging markets[J]. Pacific-Basin Finance Journal, 2014, 27(1): 49-71.

[17] Corwin S A, Schultz P. A simple way toestimate bid-ask spreads from daily high and low prices[J]. Journal of Finance, 2012, 67(2): 719-759.

[18] Fong K Y, Holden C W, Trzcinka C. What are the best liquidity proxies for global research[R]. Working Paper, SSRN, 2013.

[19] Chordia T, Roll R, Subrahmanyam A. Market liquidity and trading activity[J]. Journal of Finance, 2001, 56(2): 501-530.

[20] Amihud Y, Mendelson H, Lauterbach B. Market microstructure and securities values: evidence from the Tel Aviv Stock Exchange[J]. Journal of Financial Economics, 1997, 45(3): 365-390.

[21] Amihud Y. Illiquidity and stock returns: cross-section and time-series effects[J]. Journal of Financial Markets, 2002, 5(1): 31-56.

[22] Florackis C, Gregoriou A, Kostakis A. Trading frequency and asset pricing on the London Stock Exchange: evidence from a new price impact ratio[J]. Journal of Banking & Finance, 2011, 35(12): 3335-3350.

[23] Swinscow T. Statistics at square one[M]. London: BMJ Publishing Group, 1997.