随机和模糊环境下绿色供应链网络优化设计
贾旭,刘诚
(中南大学 数学与统计学院,湖南 长沙 410083)
绿色供应链是一种在整个供应链中综合考虑环境影响和资源效率的现代管理模式,绿色供应链概念起源于Webb在1994年提出的绿色采购概念,最早由美国密歇根州立大学的制造研究协会在1996年进行一项“环境负责制造(ERM)”的研究中提出,并认为绿色供应链要将环境因素整合到供应链中产品设计、采购、制造、组装、包装、供应链和分配等各个环节中。 Srivastava[1]在绿色供应链管理综合评论中提出了2种“绿色”模式:绿色产品的设计和绿色供应链的运作。传统的供应链网络设计问题是探究能使供应链长期运作的最优决策,它以确定性的线性模型为主,在此基础上,Aghezzaf[2]在供应链网络中考虑了税费问题并加入风险管理。但是上述文献大都是在确定的条件下探究供应链的网络优化设计问题,实际供应链网络设计的参数如固定建设费用、运输费用和需求等通常都是不确定的。参数的不确定性会对供应链网络在经济和环境2个方面的整体表现产生显著的影响,在供应链网络设计中忽略不确定性将会使企业面临巨大的风险。大多数文献采用随机规划理论处理供应链网络设计中的不确定性问题。Awudu等[3]探究了价格和需求是随机条件下的三级供应链规划问题,Osmani等[4]研究了多种因素是随机条件下的多原料网络设计问题,Santoso等[5]建立了随机条件下供应链网络规划模型比较完全的考虑了供应链运作中的各种随机性,Majid等[6]研究了逆向物流设计的多目标随机模型,上述模型考虑到供应链运作过程中的部分不确定性并且建立了多目标优化模型,然而没有结合绿色供应链的决策来研究整个物流网络的运作,WANG等[7]充分考虑了多产品背景下供应链运营中的经济效益和生态效益,在供应链网络规划设计的同时考虑到碳的排放量。文献[8]运用模糊规划的方法探究了运输和商品包装处理过程中碳的排放量,并用模糊参数的期望来表示碳的排放量。在实际供应链网络操作中很多参数如固定建设费用、运输费用和需求量等通常都是不确定的。参数的不确定性会对供应链网络在经济和环境2个方面的整体表现产生显著的影响,在供应链网络设计中忽略不确定性将会使企业面临巨大的风险。利用随机规划理论来描述不确定性依赖于精确的历史统计数据,在实际生产中企业都对供应链网络中每个时期的费用参数、分销商的需求量和加工商品所占空间的大小等都有着较为完整的记录,通过大量的数据统计容易获得这些参数的不确定性随机分布。而碳的排放量易受生产环境、气候变化、生产周期等各种因素的影响,无法获得受单一变量控制的随机分布,随着生产经营过程的日益复杂,产品生命周期大大缩短,工厂的供应量几乎无法获得精确的历史统计数据,因此在一些实际应用中使用随机规划方法来描述碳的排放量和工厂供应量有其局限性,而模糊数学规划可以处理由于决策者缺少对参数真实值的知识而带来认知上的不确定性问题。本文考虑多产品背景下三级供应链运营中的经济效益和生态效益,建立随机和模糊环境下绿色供应链多目标优化模型,第1个目标函数主要探究了供应链的网络优化问题,在随机环境下建立供应链网络优化模型;第2个目标函数在模糊环境下建立碳排放量模型;第3个目标函数在第1个目标函数的基础上建立方差函数;第4个目标函数引入成本风险模型;运用随机规划和模糊规划理论处理目标函数中的不确定性,并通过概率统计方法和模糊统计方法分别计算随机参数的置信区间和模糊参数的隶属度,把随机机会约束和模糊机会约束清晰化,得到确定性的多目标函数。最后用分层次法、ε−约束法和加权的理想点法相结合来求解多目标模型。
1 问题的描述和符号说明
1.1 问题的描述
本文的供应链网络包括工厂、配送中心和分销商,工厂给配送中心发货这一环节称为运输,配送中心给分销商运货这一环节称为配送,每个工厂制造多种类型的商品,生产过程不产生二氧化碳,工厂把商品运送到配送中心,由配送中心负责对商品实行配送和再加工,加工过程中产生二氧化碳,每种商品可以使用多种加工技术,一般来说,越环保的技术其成本也越高,通过多个配送中心将商品配送到各分销商处。分销商和工厂的位置是已知且固定的,由于在候选地点选取配送中心对供应链网络的成本和碳的排放量具有很大的影响,因此建立配送中心的固定费用按照环保水平分成不同的等级。
采用基于Eco-indicator99数据库的二氧化碳排放量作为衡量指标。二氧化碳排放量是衡量各种温室气体对地球温室效应贡献度的一个基本单位,可以将不同温室气体的排放折算成对应的二氧化碳排放量用于统一度量整体温室效应的结果。因此只考虑二氧化碳的排放量作为唯一影响环境的气体,根据国际气候变化专门委员会报告中(iPCC2007)所提出的方法,使用 ECO-it1.4软件及其数据库对商品生命周期中的二氧化碳排放量进行计算[9]。本文使用的是iPCC2007方法中的100年期的时间表。
实际供应链网络系统中,决策者通常无法全面掌握物流网络设计的确定信息,很多参数都是随机和模糊的。因此本文假设如下参数是随机的:商品的运输费用和配送费用、配送中心商品的加工费用、分销商的缺货费用,加工商品所占空间的大小以及分销商的需求量等,通过对数据的统计分析容易获得参数的随机分布;模糊参数为:商品在配送中心加工过程中碳的排放量、运输和配送过程中碳的排放量、以及每个工厂的供应量等,这些参数可以用三角模糊数表示。随机分布和三角模糊数能够较为准确的表示参数的不确定性比较贴近实际情况,且形式简单易于操作。
1.2 符号说明
I:工厂的总数量;(i=1, 2, …, I);J:配送中心的总数量;(j=1, 2, …, J);K:分销商的总数量;(k=1,2, …, K);S:场景组成的集合;(s=1, 2, …, S);R:商品的种类总数;绿色环境保护水平的种类总数:运输过程中第r种商品的二氧化碳释放量,为三角模糊数;:配送过程中第r种商品的二氧化碳释放量,为三角模糊数;:工厂i对第r种商品的供应量,为三角模糊数;:第s种场景下配送中心j对商品r的单位处理费用;:第s种场景下第r种商品的运输费用;:第s种场景下第r种商品的配送费用;:第s种场景下分销商k第r种商品单位缺货的惩罚费用;销售商k对第r种商品的需求量;:单位第r种商品在配送中心j的占用空间;配送中心j选择第l种绿化水平的固定投资费用:工厂i到配送中心j运送第r种商品的运输量;配送中心j到分销商k运送第r种商品的配送量;:分销商k对第r种商品的缺货量; H:配送j中心j的容量水平:配送中心j选择第l种绿化水平后单位数量的第r种商品二氧化碳排放量;αk:置信度为95%~99%的置信区间;βj:置信度为95%~99%的置信区间; ps:场景s发生的概率;

2 模型的建立和转化
2.1 模型构建
与传统的供应链网络模型不同,本文在配送中心建设的固定费用中加入了环保投资费用,固定费用按环保水平分成了若干个等级。相应的,ωj是一个0-1变量当配送中心j被选择时,ωj为1,否则为0;ωjl也是一个0-1变量,当配送中心j选择了第l种绿化水平为 1,否则为 0,要求每个配送中心只能选择一种绿化水平即:供应链网络运行中允许分销商缺货, 整个过程不考虑库存费用是一个随机向量,服从一个已知连续的概率分布。在概率论中,随机向量的一个最重要的数字特征就是期望值,期望值模型是随机规划中最常见的形式,则供应链网络优化的目标函数为:
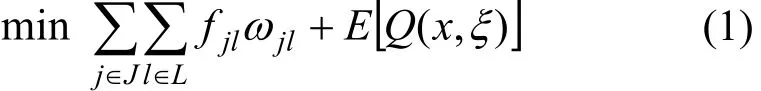
其中:

本文通过运用蒙特卡罗模拟技术来处理连续的随机分布,本文把蒙特卡罗抽样的样本称为离散的场景,每个场景都有其相应的概率Ps,用这些有相应概率的离散场景来模拟连续的概率分布函数,S表示场景的集合,则式(1)可以近似地表示为:

其中:

商品在配送中心加工过程和运输配送过程中二氧化碳排放量的目标函数为:
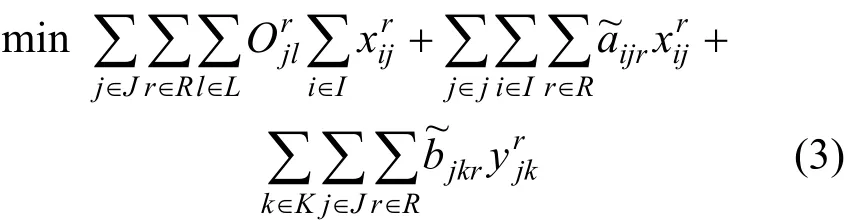
为了增加模型的稳定性,本文引用了成本费用的方差模型:
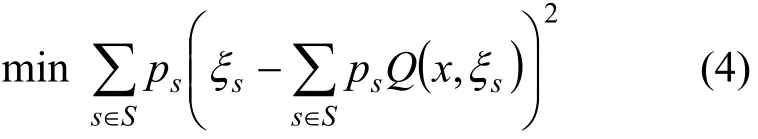
供应链网络成本费用的不确定性可以通过不满足预算费用的最小可能性函数,这里称其为风险函数:

us是第s种场景下的一个0-1变量:
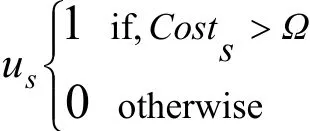
Ω代表预算费用,Costs表示第s种场景下的总成本费用。
约束条件:
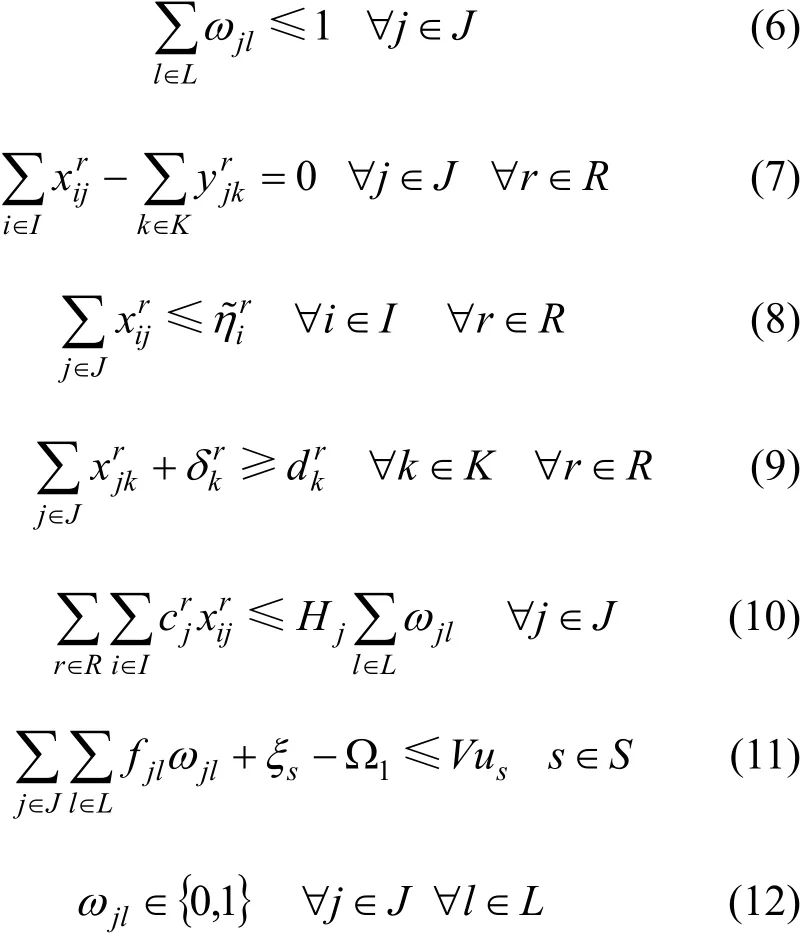
约束(6)表示每个被选择了的配送中心只能选择一种绿化水平,约束(7)为商品流通量约束,模型讨论的是一个单独的时间段所以在配送中心没有库存,约束(8)为工厂i给配送中心j的第r种产品的运货量不多于工厂i的供应量,约束(9)表示配送中心j对第r种产品供给量与第k个分销商的缺货量之和应该大于第k个分销商的需求量,其中为服从正态分布的随机参数,约束(10)表示配送中心的生产空间限制,其为服从正态分布的随机参数,约束(11)表示如果供应链网络成本费用大于预算费用则 us为1,如果供应链网络成本费用小于预算费用则 us为0,约束(12)定义了约束变量的类型。
2.2 约束条件的确定化

则根据事先给定的置信水平 αk∈(0.95,0.99)和 βj∈(0.95,0.99),约束条件(9)和(10)可分别转化为:

因此,式(13)转化为普通的确定型不等式约束:

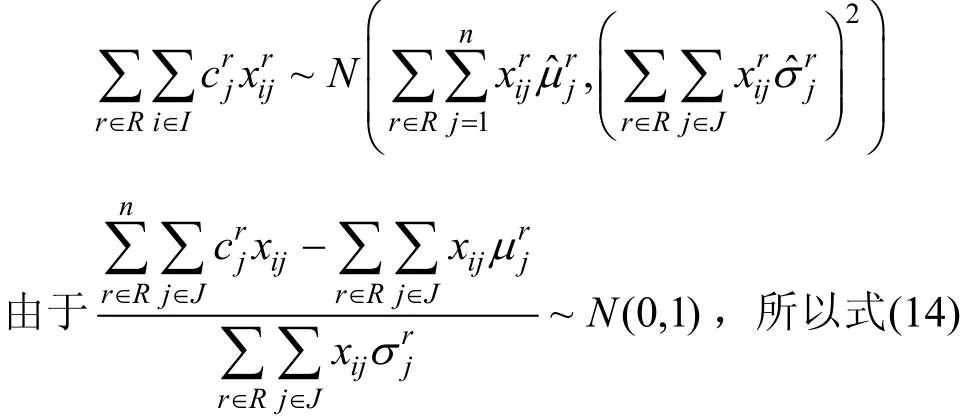
转化为普通的不等式约束:

考虑到计划范围内可用资源,机器的运转能力,工人技能,公共政策等因素的不确定性,
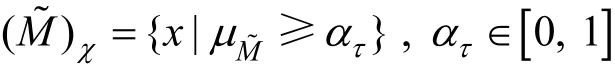


定义2[12]区间数称为区间数a≤b的满意度。其中a的中点,称为a的位置系数为a的半宽,称为a的柔性系数。
定义 3 在 λ0满意度水平下,区间型约束可为确定性约束

对于区间线性规划由定义3,有
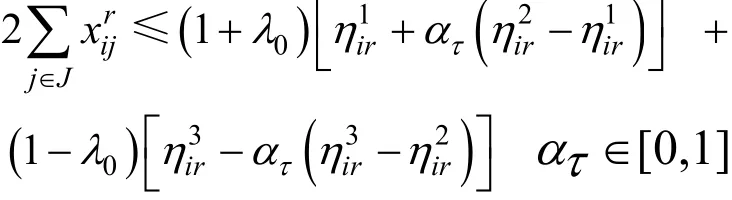
2.3 模型的清晰化
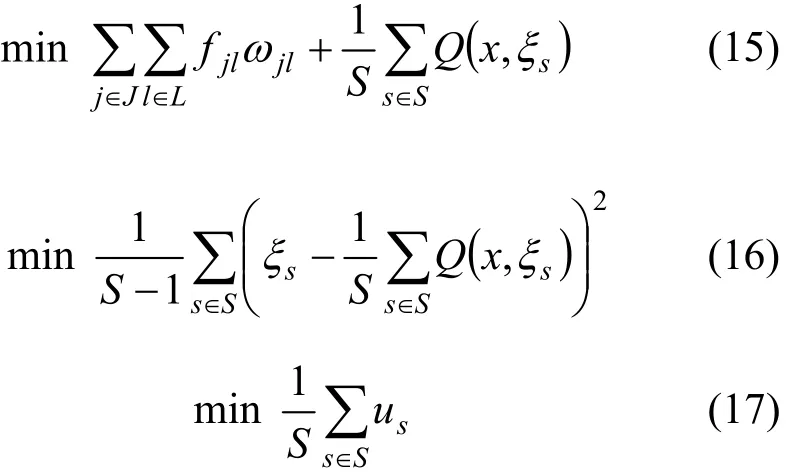
因此总费用的期望,总费用的方差和总费用的风险函数就可以分别用式(15)~(17)表示。

Pos{ · }表示{·}中事件成立的可能性。目标函数(17)和机会约束(18)表示所求的目标函数值f应该是在保证置信水平至少是γ时所取的最小值。
引理 1[15]设三角模糊数为则对任意给定的置信水平 α(0≤α≤0),当且仅当z ≥ (1-α) q1+αq2时有 P os{q ~≤z }≥α成立。
由引理1可知,目标机会约束可以转化为如下的清晰的等价类:
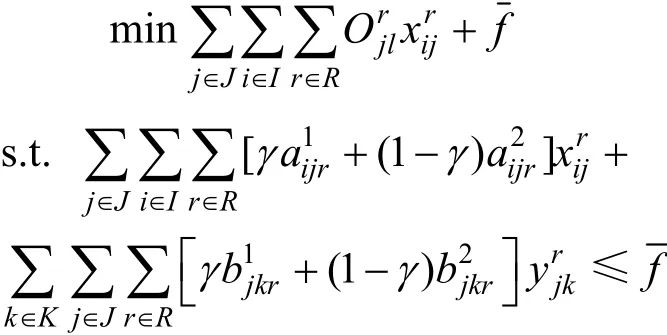
3 模型求解
不确定模型转化为清晰模型为:

其中:
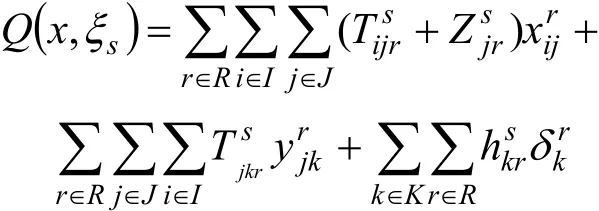
确定性约束条件:
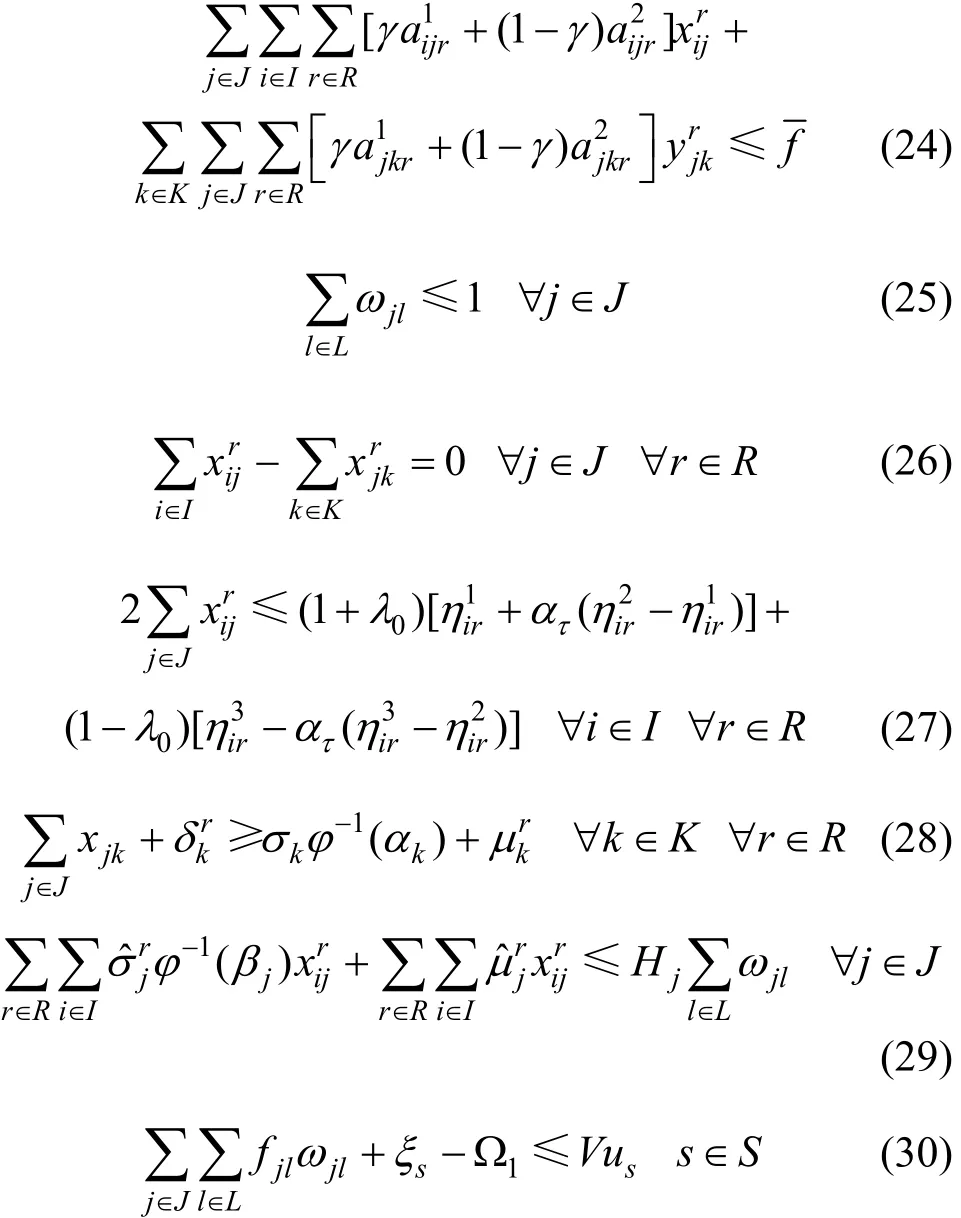
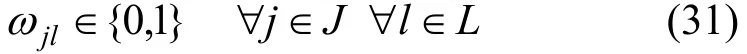
算法设计:
用分层次法、ε−约束法和加权的理想点法相结合来求解多目标模型:
步骤2:用加权的理想点法处理目标函数(20),(21)即:

步骤 3:将原多目标规划模型转化为如下单目标函数:

s.t. (24)~(31)

步骤4:求解单目标函数。
步骤5:调整ε3,ε4的值重复步骤2,3,4。
步骤6:选择一组有效解。
4 数值算例
4.1 算例描述
某空调制造商计划在一地区为2种类型的空调开拓市场,该地区拥有8个分销商。制造商计划设计供应链网络以满足这些分销商的需求,该供应链包括工厂、配送中心和分销商3个层次,如图1所示。分销商对2种类型空调的需求服从正态分布,需求量的期望见表1。已知制造商目前有6个候选配送中心,2个工厂,每个工厂的供应量是一个三角模糊数见表2,每个候选配送中心建设时有3种环保水平可供选择,每种环保水平下建设配送中心的固定费用见表 3,每种环保水平下碳的释放量见表4。

图1 供应链Fig. 1 Supply chain

表1 客户的需求量Table 1 Customer demand 万件
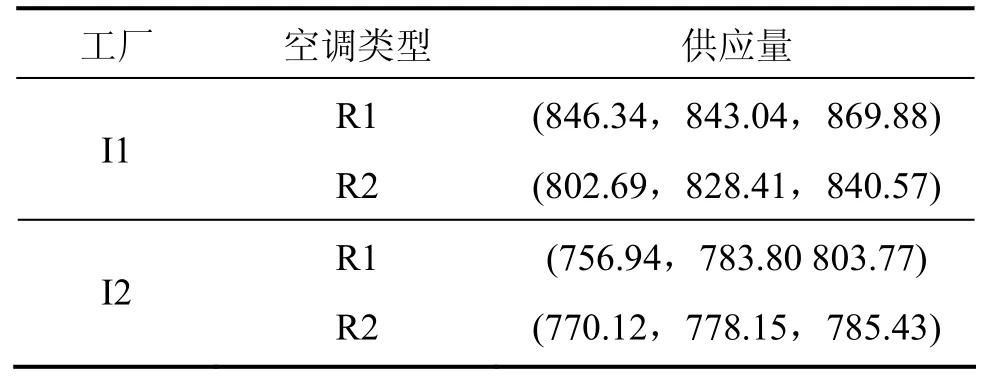
表2 工厂的供应量Table 2 Factory supply 万件

表3 每种环保水平下建设配送中心的固定费用Table 3 Fixed cost of construction distribution center under each kind of environmental protection level 万元
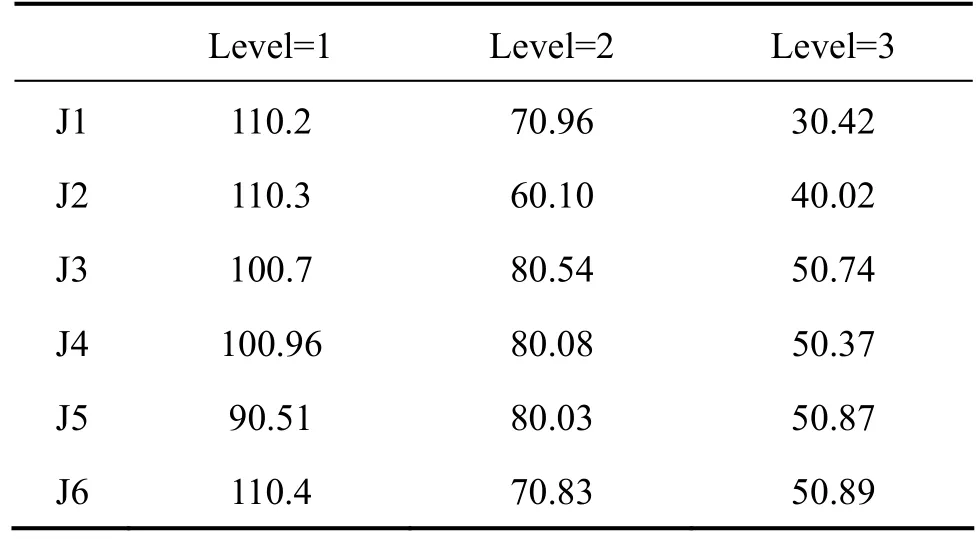
表4 环保水平l下碳的释放量Table 4 CO2 emissions at environmental level l t
4.2 算例结果
利用 LINGO软件,依据设计的算法编程,根据求解步骤进行求解,得到了一系列的 Paretooptimal解。本节列出当 λ1=λ2=0.5时模型的一组解:工厂到配送中心运送第r种产品的运输量见表5,配送中心到分销商运送第r种产品的运输量见表6,分销商k对第r种商品的缺货量见表7,ωjl的取值见表8。
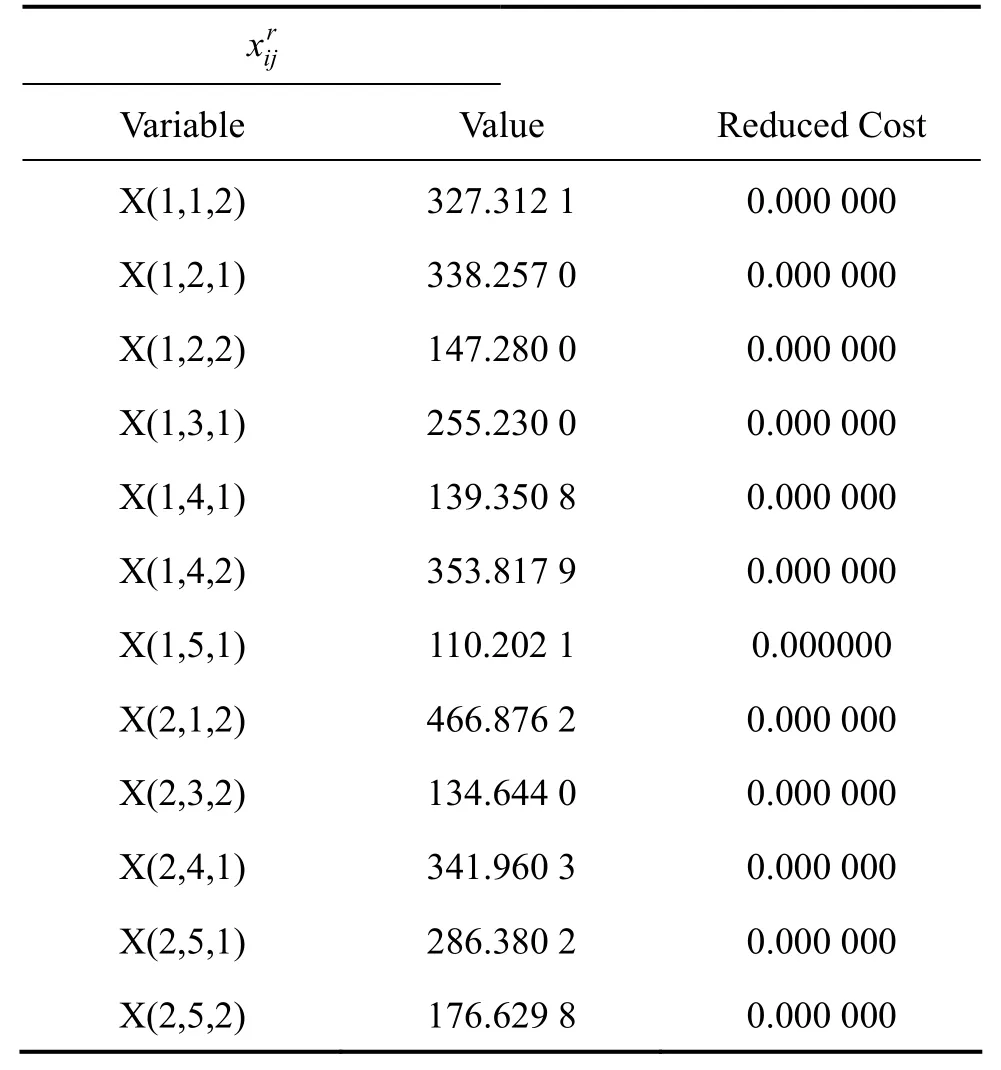
表5 工厂到配送中心运送第r种产品的运输量Table 5 Transport volume of the product r from plant to distribution center
当λ1=λ2=0.5时,目标函数的最小值为0.122 484 7,相应的供应链网络费用为988.739 4万元,二氧化碳的排放量为0.154 8万t。
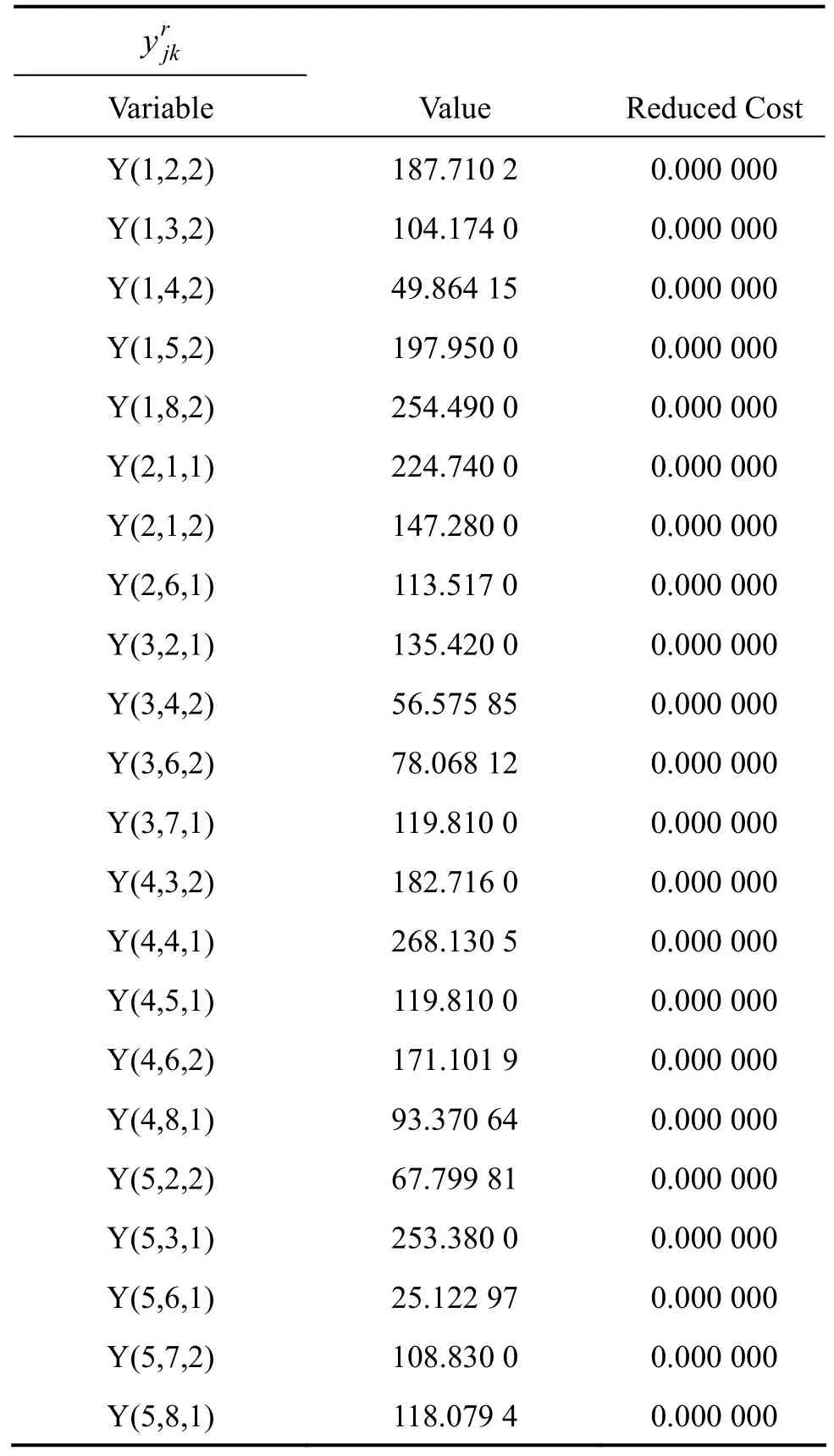
表6 配送中心到分销商运送第r种产品的运输量Table 6 Transport volume of product r from distribution center to distributor

表7 分销商k对第r种商品的缺货量Table 7 Shortage of product r for distributor k
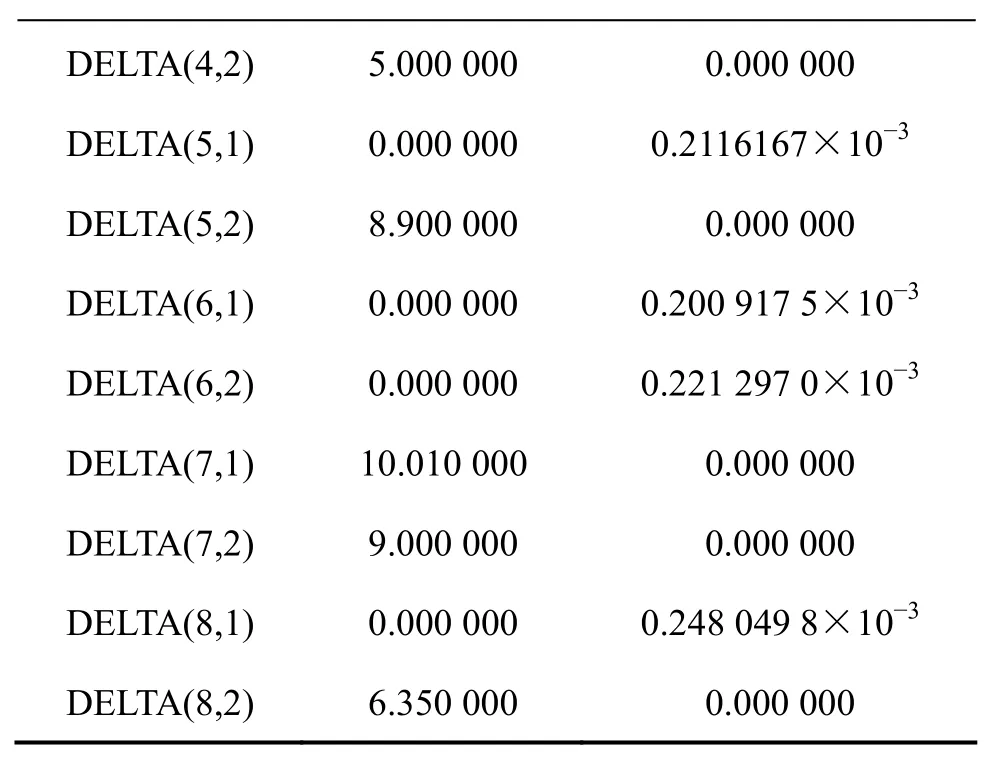
DELTA(4,2) 5.000 000 0.000 000 DELTA(5,1) 0.000 000 0.2116167×10−3 DELTA(5,2) 8.900 000 0.000 000 DELTA(6,1) 0.000 000 0.200 917 5×10−3 DELTA(6,2) 0.000 000 0.221 297 0×10−3 DELTA(7,1) 10.010 000 0.000 000 DELTA(7,2) 9.000 000 0.000 000 DELTA(8,1) 0.000 000 0.248 049 8×10−3 DELTA(8,2) 6.350 000 0.000 000
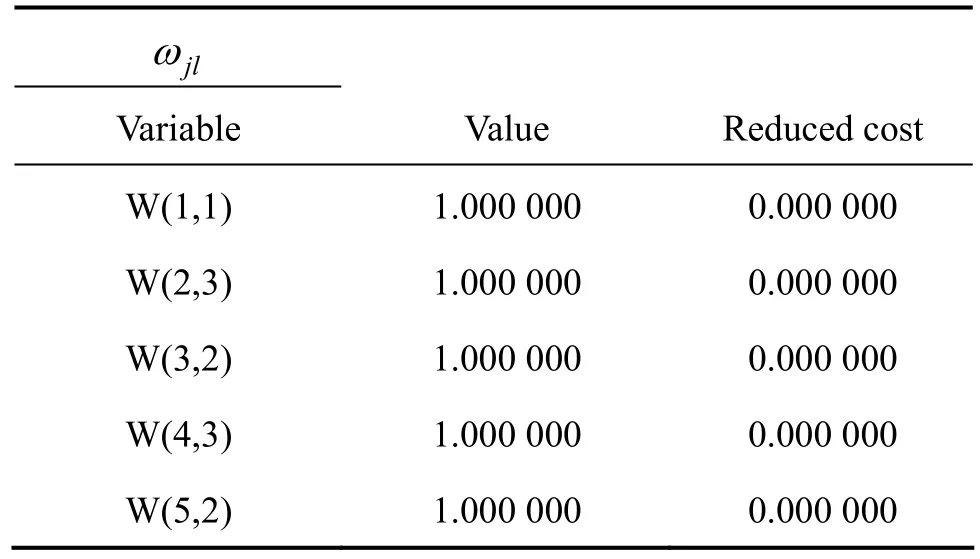
表8 jlω的取值Table 8 Value of jlω
4.3 灵敏度分析
当λ1分别取0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9 时,(即 λ2取 0.9,0.8,0.7,0.6,0.5,0.4,0.3,0.2,0.1)相应的目标函数值图 2、供应链网络费用见图 3,碳的排放量见图 4,供应链网络费用与碳的排放量的关系如图5。

图2 目标函数值Fig. 2 Value of he objective function
如图2所示,目标函数值随着λ1的增大呈现先增后减的趋势,而λ1在0.3~0.5之间时,这一趋势变化比较缓慢,由图3所示,供应链网络费用随着λ1的增大而减小,但λ1大于0.4时,这种减小趋势越来越平缓,图4所示碳的排放量随着λ1的增大而增大,趋势变化类似正比例函数且在 λ1为 0.4~0.6这一区间较为平缓。决策者如果偏好于环境的绿化水平,那么可以选取较小的λ1值,但是这需要花费大量的环保费用;如果偏好于费用最小化可以选取较大的λ1值,但是这需要付出一定的环境代价;图5更加清晰地显示了最小化总成本和最小化总碳排放量这2个目标之间存在的冲突关系,当碳排放量从0.175万t减小到0.15万t左右时,供应链网络费用明显少于相对于碳排放量从 0.15万 t减小到0.13万 t时的费用,且 0.15所对应的值正好在0.3~0.5之间。综上所述,均衡供应链网络的费用和环境保护问题的角度λ1应当在0.4~0.6取值。
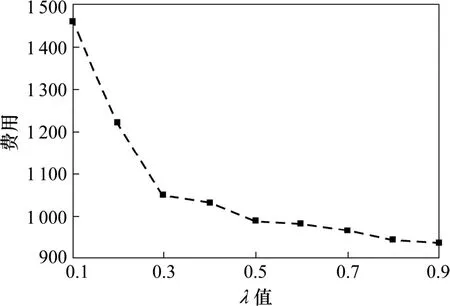
图3 供应链网费用Fig. 3 Cost of the supply chain network
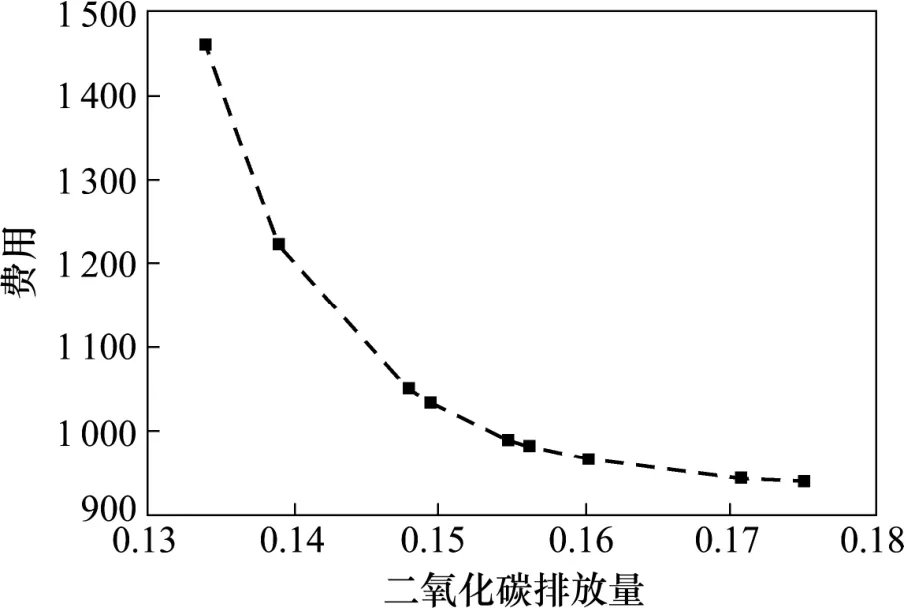
图4 二氧化碳排放量Fig. 4 Carbon dioxide emissions

图5 供应链网络费用和二氧化碳排放量关系Fig. 5 Relationship between supply chain network costs and carbon dioxide emissions
5 结论
1) 不确定环境中对供应链网络中配送中心选址问题以及生产和运输过程中二氧化碳的排放进行研究,在随机条件下以供应链总成本为目标函数,模糊环境下以碳的排放量为目标函数,建立绿色供应链网络设计的均衡模型。
2) 运用随机规划和模糊规划的相关知识将不确定性模型转化为确定性规划模型;利用分层次法、ε−约束法和加权的理想点法相结合来求解数值算例,最后通过灵敏度分析找出供应链网络碳减排投资与其产生环境效益的最佳平衡点。
3) 进一步的研究将综合考虑供应链网络参数的不确定性和动态性、战术层的库存和运输决策等特点,同时为了确保供应链网络的可持续性,除了考虑经济和环境目标,还有必要将社会影响加入到供应链网络设计问题的研究中。
参考文献:
[1] Srivastava S K. Green supply chain management: a state-of-the-art literature review[J]. International Journal of Management Reviews, 2007, 9(1): 53−80.
[2] Aghezzaf E. Capacity planning and warehouse location in supply chains with uncertain demands[J]. The Journal of the Operational Research Society, 2005, 56(4): 453−462.
[3] Awudu I, ZHANG J. Stochastic production planning for a biofuel supply chain under demand and price uncertainties[J]. Applied Energy, 2013(103): 189−196.
[4] Osmani A, ZHANG J. Stochastic optimization of a multi-feedstock lignocellulosic-based bioethanol supply chain under multiple uncertainties[J]. Energy, 2013(59):157−172.
[5] Santoso T, Ahmed S, Goetschalckx M, et al. A stochastic programming approach for supply chain network design under uncertainty[J]. European Journal of Operational Research, 2005, 167(1): 96−115.
[6] Majid Ramezani, Mahdi Bashiri. A new multi-objective stochastic model for a forward/reverse logistic network design with responsiveness and quality level[J]. Applied Mathematical Modelling, 2013, 37(1): 328−344.
[7] WANG F, LAI X, SHI N. A multi-objective optimization for green supply chain network design[J]. Decision Support Systems, 2011, 51(2): 262−269.
[8] Aghezzaf E. Capacity planning and warehouse location in supply chains with uncertain demands[J]. The Journal of the Operational Research Society, 2005(56): 453−462.
[9] 李进. 基于可信性的低碳供应链网络设计多目标模糊规划问题[J]. 系统工程理论与实践, 2015, 35(6): 12−35.LI Jin. Design of multi-objective fuzzy programming for low carbon supply chain network based on credibility[J].System Engineering Theory and Practice, 2015, 35(6):12−35.
[10] Hugo A, Pistikopoulos E N. Environmentally conscious long-range planning and design of supply chain net-works[J]. Journal of Cleaner Production, 2005, 13(15):1471−1491.
[11] Vanegas M C, Bloch I, Inglada J. Fuzzy constraint satisfaction problem for model-based image interpretation[J]. Fuzzy Sets and Systems, 2016, 286: 1−29.
[12] 孙玮珊, 杨斌. 基于模糊数学的不确定性绿色供应链网络设计[J]. 合肥工业大学学报, 2014, 37(5): 624−630.SUN Weishan, YANG Bin. Design of uncertain green supply chain network based on fuzzy mathematics[J].Journal of Hefei University of Technology, 2014, 37(5):624−630.
[13] 李立华, 符卓. 连续型物流设施选址的区间决策模型及算法[J]. 铁道科学与工程学报, 2011, 8(6): 107−113.LI Lihua, FU Zhuo. Interval decision-making model and algorithm for continuous logistics facility location[J].Journal of Railway Science and Engineering, 2011, 8(6):107−113.
[14] LIU D J, Garcia A, WANG J, et al. Kinetic monte carlo simulation of statistical mechanical models and coarse-grained mesoscale descriptions of catalytic reaction–diffusion processes: 1D nanoporous and 2D surface systems[J]. Chemical Reviews, 2015, 115(12):5979−6050.
[15] 陈则辉, 刘诚. 不确定环境下应急物资配送问题研究[J]. 铁道科学与工程学报, 2014, 11(5): 82−89.CHEN Zehui, LIU Cheng. Research on dispatching problem of emergency materials under uncertain environment[J]. Journal of Railway Science and Engineering, 2014, 11(5): 82−89.
——《2013年中国机动车污染防治年报》(第Ⅱ部分)

