基于安全合流概率的加速车道长度计算模型
李霞,朱志强,崔洪军,李霖
(河北工业大学 土木与交通学院,天津 300401)
在高速公路基本路段上,主线交通流比较稳定,通行能力基本可以满足设计需要,而在合流区,不合理的加速车道长度常常会引起加速车道车辆强行变道、违规超车等行为,造成主线的交通紊乱,甚至引发交通事故。Iwasaki等[1]研究指出,合流区加速车道长度的不合理设置是交通事故频发的重要原因。这一研究表明合流区路段长度是路线设计中一个重要的参数。因此,有必要对合流车辆的汇入特征及加速车道长度进行研究。Michael等[2−4]对合流区路段的合流行为进行了建模研究;李文权等[5−6]分别对合流区车辆汇入模型和加速车道长度设计进行了实例研究;李硕等[7]对合流区加速车道长度设计和车辆控制进行了建模分析。驾驶员的合流行为、车辆的安全合流概率及加速车道长度很大程度上取决于临界间隙的大小,上述研究通常假设合流过程中临界间隙为某一固定值(当主线车头间距大于该值时,加速车道车辆进行合流),但未对该值进行具体分析。结果可能与实际不相符。Pollatschek等[8−9]研究指出临界间隙随着等待延误时间的增加而减小。关羽等[10]提出临界间隙随着车辆在加速车道上行驶距离的增加线性减少。这些研究都说明临界间隙会受到道路结构及主线交通状况的影响。因此,对临界间隙的研究仍具有实际意义。基于此,笔者将描述加速车道上车辆的行驶特征,建立加速车道车辆合流过程的驶入模型,推导加速车道长度的相关计算公式,对临界间隙进行较为系统的量化分析,并用实例计算车辆在不同车流量条件下的安全合流概率,以期实现对加速车道安全长度的合理设计。
1 汇入模型建立
根据对多条高速公路加速车道上车辆的合流行为的观测及相关文献[11],车辆进入加速车道以后,欲安全汇入主线,需先加速到某一速度以缩小与主线车辆的速度差,使其保持低于主线车辆的某一速度,然后匀速行驶,当主线外车道车流出现可汇入间隙时,便立即实施变道行为,否则,需继续在加速车道上行驶以等待可汇入间隙的出现,直至完全汇入主线,完成变道,如图 1所示。
模型建立前提假设:
1) 加速车道上的车辆均按上述描述过程安全汇入主线车道;
2) 所有驾驶员的驾驶特征和变道规则相同,且均符合安全驾驶;
3) 根据观测,主线车辆间隔远大于车长,因此忽略车长影响;
4) 高速公路合流区内,主线外车道车流分布形式始终保持一致。

图1 高速公路加速车道车辆合流模型Fig. 1 Vehicle merging model of on-ramp at freeway
2 车辆合流过程模型分析
加速车道上车辆的行驶过程可作如下分析:车辆先在加速段加速行驶,然后在等待合流段匀速行驶,当主线车流出现可汇入间隙时,立即汇入主线,如图1所示。
因此,车辆行驶距离的计算公式为:

式中:La和 Lb分别为加速段、等待合流段的行驶距离。
2.1 加速段行驶距离
加速段行驶距离的计算公式为:[12]

式中:a为车辆在加速段 La的平均加速度,《公路路线设计规范》(JTG D20—2006)里的建议值为0.8~1.2 m/s2;V1为加速车道车辆的平均合流速度,可按实际观测结果取值;V2为车辆驶入加速车道的初速度,可取匝道的设计速度[13]。
2.2 等待合流段行驶距离
图 2中,车辆 A为加速车道上等待合流的车辆,其在位置1达到平均合流速度,然后匀速行驶至位置2,从1到2行驶的路程即为等待合流段行驶距离Lb,B,C和D代表不同的主线车辆,其中,在车辆A等待合流的过程中,车辆B……C从主线超过A。

图2 车辆等待合流过程Fig. 2 Process of vehicles waiting for merging headway
假设期间共经过n−1个不可汇入间隙,第n个间隔恰好为第1次出现的可汇入间隙。则等待合流段行驶距离为:

式中:Va为车辆合流后的主线平均行驶速度,可按实际观测结果取值;d为主线车辆的平均间距,可按下式进行计算。

式中,q为高速公路主线外车道车流量,可在400~600 veh/h之间取值。
3 临界间隙研究
主线外车道车流量、驾驶员自身特征、车辆特征、驾驶员视野等都会影响到驾驶员对临界间隙的判断。本文假设驾驶员对临界间隙的判断值相同。车辆进入加速车道后,驾驶员开始依据这一判断值对可汇入间隙进行预估,当出现大于临界间隙的间隔时,立即汇入,否则,要继续等待可汇入间隙的出现。
3.1 车辆合流完成时刻车距模型
假设M车已从加速车道汇入主线,M车跟前面的M+1车保持距离l1,若M+1车遇突发状况减速,经过一段反应时间后,M车的驾驶员也开始减速,若2车均静止后依然能保持安全距离l,说明2车在行驶过程中保持的距离l1属于安全跟车距离,M车可以安全合流,如图3所示。
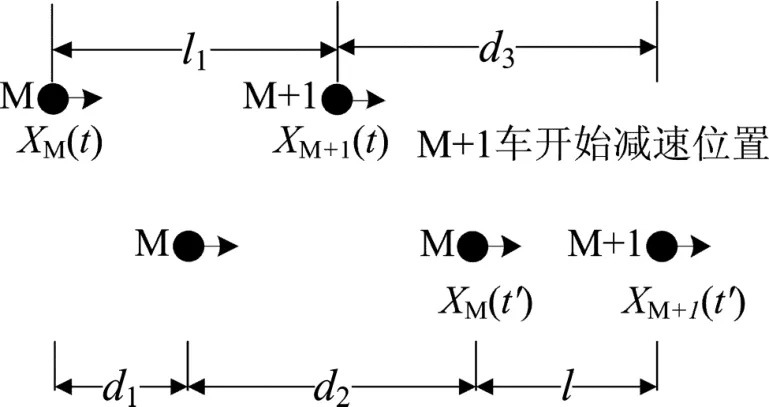
图3 合流车辆与前车距离模型Fig. 3 Model of the distance between the merging vehicle and the forward

同理,当M车与紧随其后的M−1车均静止时也能保持安全距离 l,则 2车在行驶过程中保持的距离l2也属于安全跟车距离(考虑到M车的转向灯提醒,M−1车驾驶员可以随时减速,故忽略 M−1车驾驶员的反应时间),如图4所示。


式中:VM为M车平均车速,可按实际观测结果取平均值;l1为M+1车和M车在t时刻的间距;d1为 M 车驾驶员反应过程中车辆的行驶距离;d2和d3分别为M车M+1车的制动距离;l为前后2车均静止时的安全距离,根据相关文献,可取值为 5 m[14];l2为M车和M−1车在t时刻保持的间距;d2′和 d3′分别为 M−1车、M 车的制动距离;tf为驾驶员的反应时间,根据相关文献,可取值为2.5 s[15]。

图4 合流车辆与后车距离模型Fig. 4 Model of the distance between the merging vehicle and the backward
3.2 确定临界间隙
临界间隙是驾驶员对主线外车道车头间距判断接受的理论值,而车头间距是主线外车道交通流中的随机值。当临界间隙较小时,主线车流车头间距大于该间隙的概率较大,所需的加速车道较短;反之,较长。车头间距和临界间隙是影响加速车道长度的重要因素。在其他因素统一的情况下,较大的车头间距与较小的临界间隙所对应的等待合流段行驶距离较短,反之,较长。因此,对车辆临界间隙的研究对车辆的安全合流及加速道长度的设计尤为重要。
车辆完成安全合流需要2个必要条件:1)合流后的车辆需要与前车保持至少l1的距离且与后车保持l2的距离;2)为保证车辆在合流过程中不刮蹭到后车,车辆合流完成之后与后车保持的跟车距离l2要大于合流过程行驶距离,如图5~6所示。
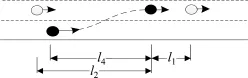
图5 安全合流模型Fig. 5 Security merging model

图6 不安全合流模型Fig. 6 Dangerous merging model
根据相关文献[16]及驾驶员经验,汽车在高速公路上变道,若速度为80 km/h,方向盘需旋转1/8圈,汽车偏移角度为5°,如图7所示。

图7 车辆合流过程Fig. 7 Process of merging vehicle
则:

式中:D为单车道宽度,可取值为3.75 m[16];m为车辆合流过程所需距离;Smin为主线车辆的临界间隙。
4 加速车道长度与安全合流概率关系
为了更好地理解加速车道上车辆的合流过程,本文引入安全合流概率这一概念,即针对某一入口匝道而言,在一定的距离内,在不引起交通冲突的前提下,若干辆行进在加速车道的车辆中能够安全变道至主线外车道的车辆数的占比。由于高速公路主线路段的交通量一般较城市道路路段小,其主线交通流量较低,可认为车头间距服从负指数分布[18]。
那么,车头间距d的概率分布为:

则外车道上任意一个可汇入间隙出现的概率:
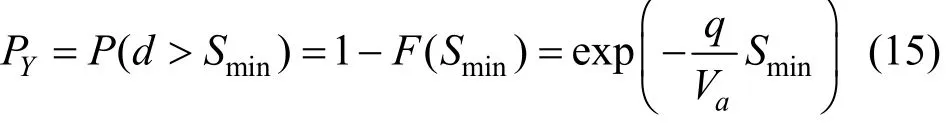
那么在第n个间隔第1次出现可汇入间隙的概率为:

变道车辆必须满足L+Ls≤Lx,才能保证车辆安全汇入主线,则:

即:
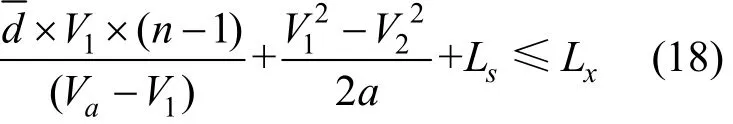
则上式便是关于n的条件不等式,即n必须满足上述条件时,合流车辆才能安全汇入主线。其中,Ls为渐变段长度,取值可参照《公路路线设计规范》(JTG D20—2006);Lx为加速车道长度,此处可令Lx=L+Ls。
由于n的取值是离散随机的,因此可以建立关于n的分布律。表1中可汇入间隙出现的概率之和即为加速车道上车辆的安全合流概率。

表1 不同车辆间隔下加速车道长度及合流成功率Table 1 Acceleration lane length and merging probability of different vehicle headways
5 加速车道长度设计
为了获得高速公路加速车道车辆的平均合流速度与合流后的主线平均行驶速度,笔者在荣乌高速公路天津段入口处进行了一系列数据采集工作,测速仪器采用BUSHNELL VELOCITY手持雷达测速仪,调查时间为 2016−12−12,利用早高峰7:00—10:00和晚高峰16:00—20:00 2个时间段,选取80组有效数组,如图8所示。

图8 车辆合流速度与合流后速度散点图Fig. 8 Scattergram of the speed of merging vehicles and vehicles after merging
根据调查结果,车辆的合流速度V1与合流后的主线车速Va属于一次线性相关,对数据进行回归分析得到:

结合式(16),(18),(19)及相关物理量,可求得当高速公路主线外车道车流辆 q=400,500和 600 veh/h时,加速车道长度与安全合流概率之间的概率关系。其中,V1=66 km/h,Va=90 km/h,V2=50 km/h,D=3.75 m,l=5 m,tf=2.5 s,a=1.2 m/s2。由于模型假设高速公路外车道车流量是随机的,根据随机概率事件,此图应该是跳跃阶梯型曲线,但在实际情况下,安全合流概率是随加速车道长度呈递增的平滑曲线,因此可将其拟合成具有实际意义的平滑曲线,如图9所示。
由图9可知,当加速车道长度取为350 m时,安全合流概率基本可达90%,在此基础上,再增加其长度,不会对合流概率有太大提升。少数合流车辆因找不到可汇入间隙可在末端停车观察,以等待可汇入间隙的出现。因此,90%的安全合流概率已可保证大部分加速车道车辆顺利完成合流,而不会造成主线车辆的交通冲突。此外,按照此概率下的加速车道长度进行施工一定程度上也可以节约施工成本;当加速车道长度小于150 m时,安全合流概率均低于50%,合流车辆有可能采取违规超车、强行变道等行为,造成主线交通紊乱,延误增大,甚至引发交通事故。结合图 9与式(18)仿真出来的结果,即可求得加速车道应当设计的长度。

图9 加速车道长度与安全合流概率关系Fig. 9 Relationship between the length of acceleration lane and security merging probability
6 结论
1) 基于安全合流概率的加速车道长度设计,丰富了计算方法,完善了理论模型和领域知识,其计算结果可为规范的制定和修改提供参考。但也存在一定不足:受到主线交通量的限制,只能假设主线交通流服从负指数分布,需在以后完善车辆合流模型跟计算方法;由于实际条件所限,文中仅在同一天的早晚高峰2个时间段采集了数据,可能导致结果出现偏差。因此,在实际的加速车道长度设计中,考虑到不同高速公路路段的道路状况、交通条件的差异性,还需在多个工作日的不同时间段(早晚高峰段及平峰段)做运行速度的调查、预测等工作,以获得更加准确、可靠的数据。
2) 主线外车道车流量能显著影响车辆的合流成功率,在加速车道始段,主线外车道车流量越大,安全合流概率越小。随着加速车道的增长,合流成功率的增加变慢,最终将趋于平缓。这些结论对加速车道安全长度的设计及匝道车辆的合流行为具有理论指导作用。
参考文献:
[1] Iwasaki M, Sekine I, Tajima H. An analysis of traffic accidents at diverging and merging sections on the metropolitan epressway[C]//Proceedings of Infrastructure Planning, Tokyo: Japan Society of Civil Engineers, 1992: 311−316.
[2] Michael R M, Fazio J. Driver behavior model of merging[J]. Transportation Research Record: Journal of the Transportation Research Board, 1989, 1233(6): 4−10.
[3] Makigami Y, Matsuo T. Merging probability calculation method considering multiple merging phenomena[C]//Proceedings of the 11th International Symposium on Transportation and Traffic Theory, New York: Elsevier,1990: 21−38.
[4] Chin H C, Quek S T, Cheu R L. Traffic conflicts in expressway merging[J]. Journal of Transportation Engineering, 1991, 117(6): 663−643.
[5] 李文权, 王炜, 邓卫, 等. 高速公路加速车道上车辆的汇入模型[J]. 中国公路学报, 2002, 15(2): 95−98.LI Wenquan, WANG Wei, DENG Wei, et al. Merging model of vehicle on freeway acceleration lane[J]. China Journal of Highway and Transport, 2002, 15(2): 95−98.
[6] 李爱增, 李文权, 王炜. 城市快速路互通立交最小间距[J]. 公路交通科技, 2008, 25(6): 104−110.LI Aizeng, LI Wenquan, WANG Wei. Minimum interchange spacing of urban expressway[J]. Journal of Highway and Transportation Research and Development,2008, 25(6): 104−110.
[7] 李硕, 张样. 高速公路主线流量对入口加速车道设计影响分析[J]. 中国公路学报, 2000, 13(2): 108−111.LI Shuo, ZHANG Yang. An application study of merging theory on designing acceleration lane for expressway[J].China Journal of Highway and Transport, 2000, 13(2):108−111.
[8] Pollatschek M A, Polus A, Livneh M. A decision model for gap acceptance and capacity at intersections[J].Transportation Research: Part B, 2002, 36(7): 649−663.
[9] Polus A, Lazars S, Livneh M. Critical gap as a function of waiting time in determining roundabout capacity[J].Journal of Transportation Engineering, 2003, 129(5):504−509.
[10] 关羽, 张宁. 可变临界间隙条件下的加速车道车辆汇入模型[J]. 公路交通科技, 2010, 27(6): 117−120, 126.GUAN Yu, ZHANG Ning. Vehicle merging model for acceleration lane under condition of changeable critical headway[J]. Journal of Highway and Transportation Research and Development, 2010, 27(6): 117−120, 126.
[11] 邵阳, 潘兵宏, 王云泽. 高速公路互通式立交连续出口和入口间距研究[J]. 铁道科学与工程学报, 2016, 13(8):1642−1651.SHAO Yang, PAN Binghong, WANG Yunze. Study on adjacent exit and entrance distance of freeway interchanges[J]. Journal of Railway Science and Engineering, 2016, 13(8): 1642−1651.
[12] 何雄君, 梁会, 王建平, 等. 我国互通式立交变速车道长度的确定方法研究[J]. 武汉理工大学学报(交通科学与工程版), 2005, 29(3): 370−373.HE Xiongjun, LIANG Hui, WANG Jianping, et al. A study of determination of shift lane length for interchanges[J]. Journal of Wuhan University of Technology: Transportation Science & Engineering Edition, 2005, 29(3): 370−373.
[13] 李明, 张海忠, 魏为成. 厦门机场路东坪山地下立交变速车道设计探讨[J]. 公路交通技术, 2011(2): 18−22, 26.LI Ming, ZHANG Haizhong, WEI Weicheng. Probe into design of underground overpass speed-change lanes Xiamen airport road in Dongping mountain[J].Technology of Highway and Transport, 2011(2): 18−22,26.
[14] 魏丽英, 隽志才, 田春林. 驾驶员车道变换行为模拟分析[J]. 中国公路学报, 2001, 14(1): 79−82.WEI Liying, JUAN Zhicai, TIAN Chunlin. Simulation analysis of driver’s lane-changing behavior[J]. China Journal of Highway and Transport, 2001, 14(1): 79−82.
[15] 徐锦强, 陈竹师, 丁艺. 基于驾驶行为的车道变换模型研究及仿真[J]. 华东交通大学学报, 2011, 28(6): 68−72.XU Jinqiang, CHEN Zhushi, DING Yi. A model study and simulation of lane changing based on driving behaviors[J]. Journal of East China Jiaotong University,2011, 28(6): 68−72.
[16] 刘伟铭, 邓如丰, 张阳, 等. 高速公路出匝分流区超车道车辆车道变换模型[J]. 公路交通科技, 2012, 29(8):106−111.LIU Weiming, DENG Rufeng, ZHANG Yang, et al.Vehicle lane-changing model for overtaking lane in freeway off-ramp diverging area[J]. Journal of Highway and Transportation Research and Development, 2012,29(8): 106−111.
[17] JTJ B01—2014, 公路工程技术标准[S].JTJ B01—2014, Technical standards of highway engineering[S].
[18] 张政. 排队论在高速公路收费系统中的应用[J]. 西安航空技术高等专科学校学报, 2006, 24(5): 49−50.ZHANG Zheng. Queening theory’s application in express way charging system[J]. Journal of Xi’an Aero Technical College, 2006, 24(5): 49−50.

