基于实物期权的物流园区规模与建设时机研究
张得志,詹庆雯,倪楠
(中南大学 交通运输工程学院,湖南 长沙 410075)
物流园区对于政府提高物流服务水平、降低成本和加强物流市场管理等方面起着重要的作用。作为区域或城市物流系统的重要组成部分,物流园区是政府物流网络中的核心组成部分。由于较长的建设期以及市场物流需求的不确定性,物流园区规划设计已成为愈加重要的战略问题[1]。Rudi等[2]提出一个多商品、产能规划和多式联运的网络规划问题。CHEN等[3]基于交通运输不确定性提出网络设计问题的综述,并介绍一系列双目标的网络设计模型的发展。Vieira等[4]从网络设计的角度研究枢纽选址问题,综合考虑运输成本和出行时间后,提出混合整数规划模型。ZHANG等[5]基于物流服务网络与用户之间的相互作用、经济规模以及CO2排放量的影响等因素,研究区域物流网络设计问题,结果表明物流园区的最优选址和规模取决于物流需求与经济。TANG等[6]提出可变容量的物流园区选址规划模型,模型的目标是确定物流园区的位置并将客户分配给已存在的园区。蔚欣欣等[7]基于需求的不确定性,以成本回收和路段更新为约束条件,运用实物期权建立交通网络设计模型。上述研究大多使用净现值(NPV)法,NPV法并没有考虑投资项目价值的变化,并且忽略推迟、放弃和扩大投资机会的不可逆以及不确定性投资环境[8]。而实物期权(RO)法显性地考虑投资过程中机会成本,吸引诸多学者进行研究。LI等[9]考虑城市人口的波动以及城市土地利用均衡,建立RO模型,研究交通运输方式的投资和选择问题。Chow等[10]研究不确定市场中运输网络的管理问题,运用RO法和动态规划方法获得灵活性的价值以及延迟和重新设计网络。Chow等[11]运用RO法提出网络设计的双层模型,上层模型是网络期权设计问题,目标是最大化网络投资扩展净现值,下层模型分解网络投资的推迟期权为单个、弧段相互作用期权。这些研究主要集中于静态模型、发展战略、功能安排、位置以及园区规模等问题,只有少数关于物流园区投资时机的研究。由于市场物流需求随时间随机波动,物流园区的投资回报随机变化。而不合理的物流园区投资时机容易导致较高的空置率,投资者更加难以回收投资成本。本文主要研究市场物流需求不确定的情境下,分别运用NPV法和RO法研究物流园区的投资时机与投资规模问题,并对比2种方法得出的投资需求临界值和不同决策;以此为基础,研究政府补贴和关键参数对投资决策的影响,并对模型加以运用。
1 模型假设
1.1 问题描述
随着外部经济环境等因素的变化,市场需求会发生随机变化,故投资过程中需要考虑市场需求的不确定性。政府需观察投资市场,并制定适当的投资决策。本研究考虑在完全垄断市场条件下,基于不确定物流需求,政府制定物流园区的投资决策,即优化投资时机和物流园区规模。对此本文作如下假设。
假设 1:市场环境是完全垄断的,即不考虑其他物流园区对本园区投资决策的影响。
假设 2:政府是物流园区的投资者,制定物流园区的投资决策,即首先确定投资规模,然后确定最佳投资时间。
假设 3:物流园区建设的位置由投资者决定,考虑成本时忽略地价对成本的影响。
1.2 基本模型
1.2.1投资成本
研究发现:随着物流园区规模的增加,平均单位建设成本减少,物流服务供应商通过协同运作降低其平均运营成本,即物流园区的建设存在建设规模经济现象和运作规模经济现象[12-14]。基于上述研究,本文同样忽略固定成本,考虑2种投资成本,即建设成本和运营成本,其成本模型为:

其中:CL和C0分别为建设成本和运营成本;λ为单位建设成本;M为预建园区的规模;ρ为规模经济影响参数;ω为与物流园区规模相关的可变运营成本。
1.2.2规模与投资时间
物流园区的单位中转费用与市场物流需求相关,并受随机需求的冲击,定义ξ(t)为时间t的中转费用,可以表述为:

其中:q(t)为市场需求的外生变量;β为将园区规模转换为等价货币单位的参数;γ为非负常数,表示线性需求函数的斜率,用于反应中转费用对园区规模的敏感性。
市场物流需求随时间的变化,定义 q(t)为在时间t的市场物流需求。假设需求服从几何布朗运动,可以表述为:

其中:η为物流需求增长率;σ为物流需求波动率;d(t)为无穷小的时间增量;dω(t)为标准布朗运动的增量。在任意时间t,dω(t)满足等,其中εt服从均值为0,标准差为1的标准正态分布。
投资价值是项目运营期间产生的生产者剩余,定义 Γ( q(t),M)表示项目的净现值,可以表述为:

其中:Δ为整个项目的建设周期;r为单位规模政府补贴系数。
通过计算式(5),可以得到:


根据实物期权理论,投资机会的价值等于其短时间 dt内的预期资本增值率,这种关系是由Bellman方程[15]表示为:

式(8)为期权价值 F( q(t),M)的Bellman方程,运用 Ito’s引理可以得到市场物流需求临界值 q*和期权价值 F( q(t),M)的表述为:


当 q <q*时,由于物流需求较低处于等待时期时,最好的策略是延迟投资。等待最佳时机投资是明智的策略,而投资价值是当时的期权价值;当q≥q*时,立即投资是最好的选择,而投资的价值就是净现值。
确定投资规模时,通过最大化投资者的内在价值来选择投资规模。假设 V( q)为执行期权所得价值函数的内在价值,即

为最大化这个内在价值,最优规模 M*必须满足式(11)的一阶条件:

结合式(9)和式(12),计算后得到最优需求临界值和最优规模分别为:

为确保结论有意义,最优需求和最优规模必须为正,即式(13)和式(14)中的参数需要满足:

将不等式组求解可知,参数需满足条件ρ>α/(α-1),并且α<2,或者需要满足条件ρ<α/(α-1),并且α>2。
通过上述模型,可以得到由传统NPV和RO法得到的需求临界值满足关系:

式(17)意味着采用 RO法得到的需求临界值总是大于NPV法得到的临界值,这是因为RO法考虑了投资过程中等待和推迟投资价值的灵活性。
2 案例分析
2.1 参数设置
通过2个案例来说明本研究的应用和贡献。案例1考虑政府补贴对物流园区投资的影响,并分析关键参数对需求临界值和最优规模的影响,案例 2将模型实际应用于A市的物流园区投资。案例相关数据如表1和表2所示。
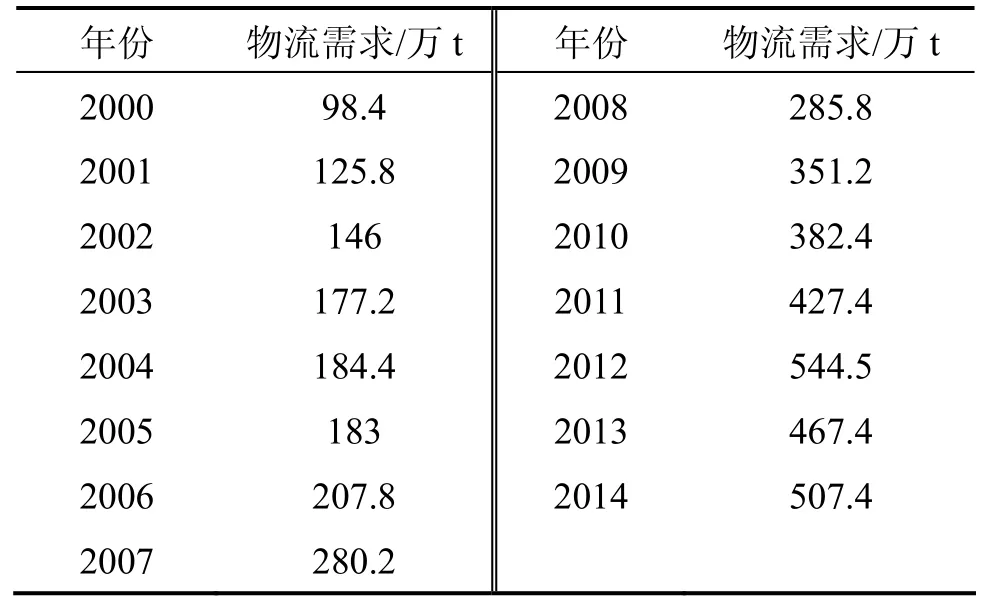
表1 物流需求Table 1 Logistic demand

表2 模型应用的输入参数Table 2 Input parameters for model application
2.2 仿真结果与分析
2.2.1政府补贴的影响
图1的交点D1,D2代表NPV法由式(7)计算得到的需求临界值和RO曲线的交点E1,E2是由实物期权法得到的需求临界值 Y*。NPV法和RO法下的需求临界值如表3所示。

图1 不同政府补贴下的NPV和期权价值曲线Fig. 1 NPV and option value curves under different government subside

表3 NPV法和RO法的需求临界值Table 3 Demand threshold for the NPV and RO
图1描述了不同政府补贴下NPV和期权价值曲线,可由式(6)和(10)计算得到。图中NPV和期权价值曲线的交点E1和E2表示由RO法得到的投资需求临界值,NPV价值曲线与横轴的交点D1和D2表示由 NPV法得到的投资需求临界值。考虑和不考虑政府补贴情况下NPV法和RO法的投资需求临界值如表3所示。由图1和表3可得到如下结论:1)无论是否考虑政府补贴,RO法得到的投资需求临界值大于NPV法得到的,这也满足式(17)的关系。例如,当考虑政府补贴时,RO法和NPV法得到的需求临界值分别为984.39万t和513.77万t,当不考虑政府补贴时,RO法和NPV法得到的需求临界值分别为1028.50万t和537.79万t。因此NPV法会导致投资者采取提前投资的决策,这也符合式(17)说明的结论;2)由于低估投资收益,不考虑政府投资会导致投资延迟。考虑政府补贴时,需求临界值为984.39万t,不考虑政府补贴时,需求临界值为1 028.50万t。考虑和不考虑政府补贴的期权价值曲线近似重合,而 NPV曲线相距较远。这是因为考虑政府补贴时的需求临界值和最优投资规模小于不考虑政府补贴,由式(10)可以看出,最优投资规模与期权价值成正比,需求临界值与期权价值成反比。因此,综合*q的负面影响和 M的正面影响使得考虑和不考虑政府补贴下的期权价值变化很小。
2.2.2关键参数的影响
1) 需求增长率η与波动率σ
由图2可知,当需求波动率不变时,需求临界值和投资规模与需求增长率成正比,因此投资者会选择更大的投资规模进行延迟投资。当需求增长率不变时,需求临界值随着需求波动率的增大而增大,这是由于投资过程中的不确定性令投资者更加谨慎,从而采取推迟投资的策略;波动率与投资规模成正向关系,即投资者面临更大的不确定性时,会选择更大的规模进行投资。

图2 η, σ对需求临界值与投资规模的影响Fig. 2 Change of the demand threshold and investment size with η and σ
2) 无风险利率k与建设周期Δ
既定无风险利率,建设周期越长,其需求临界值和投资规模越大。由于较长的建设周期意味着高的投资机会成本,从而降低了投资项目的吸引力,因此选择更大的规模、推迟投资是更好的决策策略。从图3可以看出,对于给定的建设周期,需求临界值与投资规模先与无风险利率成反比,然后与其成正比。这种变化趋势是因为低的无风险利率意味着低的投资回报,此时选择较小的规模尽早投资是较明智的决策,而当无风险利率逐渐增大时,投资成本的增长率大于回报增长率时,这意味着投资者需要承担更多的成本,因此选择较大的规模、推迟投资比较明智。

图3 k, Δ对需求临界值和投资规模的影响Fig. 3 Change of the demand threshold and investment size with k and Δ
2.3 模型运用
为进一步验证模型的有效性,将模型应用于A市的物流园区投资项目。假设 2014年以后,市场的物流需求随时间服从布朗运动,为不失一般性,根据布朗运动生成物流需求随时间变化的 3条轨迹,如图4所示。

图4 2000~2020年间市场物流需求的实际与模拟规模Fig. 4 Actual and simulated market logistic demand between 2000 and 2020

图5 A市投资物流园区时考虑政府补贴与不考虑政府补贴情况下的NPV与期权价值曲线Fig. 5 Option value and NPV of introducing logistic park with and without government subside in A city
图5(a)的NPV与期权价值曲线的交点Q表示最优投资时机为2022年,项目价值是12.93亿,交点Q是运用实物期权法根据式(14)计算得到的,而根据式(13)可知最优投资规模为 148.50万 t。NPV与横坐标的交点P表示运用传统NPV法得到的最优投资时机,其为 2014.1年,此时的市场需求为513.77 万 t。同样地,图 5(b)的 F点表示运用 RO法的最佳投资时间为2023年,其项目价值为14.01亿元,最佳投资规模为155.16 万t,NPV法的最优投资时间是2014.4年,此时市场物流需求为536.79万t。
考虑政府补贴和不考虑政府补贴时 NPV法比RO法分别提早7.9年和8.6年投资,政府补贴会使投资者选择更小的规模,较早进行投资。

表4 预估最优投资时机与投资规模Table 4 Estimated investment timings and investment size
3 结论
1) 无论是否考虑政府补贴,NPV法和 RO法的投资价值曲线之间存在较大差异,与RO法相比,传统的 NPV法低估项目投资价值,从而导致过早的投资,损失项目价值。即与NPV法相比,RO法考虑了投资过程中的不确定性与风险,会推迟物流园区投资时间。
2) 无论是NPV法或RO法,考虑政府补贴时,即政府对城市物流园区的投资进行一定补助时,会促使投资者采取较小的投资规模、较早投资的投资策略,但是如果政府不进行干预,投资者会选择更大的规模推迟投资以得到更大的投资回收。
3) 物流园区最优投资时机与最优投资规模与建设周期、无风险利率、需求增长率和波动率等重要因素相关。较高的需求增长率和较高的波动率,令投资者更加谨慎而选择更大的投资规模进行延迟投资;较长的建设周期意味着较高的投资机会成本,降低了投资项目的吸引力,因此投资者会选择较大的规模推迟投资。当无风险利率较小时,投资者会选择较小的规模更早的投资,当到达一定的临界值后,随着利率的增大,投资者又会选择较大的规模推迟投资的决策。
参考文献:
[1] Baykasoğlu A, Subulan K. An analysis of fully fuzzy linear programming with fuzzy decision variables through logistics network design problem[J].Knowledge-Based Systems, 2015, 90(C): 165−184.
[2] Rudi A, Fröhling M, Zimmer K, et al. Freight transportation planning considering carbon emissions and in-transit holding costs: a capacitated multi-commodity network flow model[J]. EURO Journal on Transportation and Logistics, 2016, 5(2): 123−160.
[3] CHEN A, ZHOU Z, Chootinan P, et al. Transport network design problem under uncertainty: A review and new developments[J]. Transport Reviews, 2011, 31(6):743−768.
[4] Vieira J G V, Fransoo J C, Carvalho C D. Freight distribution in megacities: Perspectives of shippers,logistics service providers and carriers[J]. Journal of Transport Geography, 2015, 46(5): 46−54.
[5] ZHANG D, ZHAN Q, CHEN Y, et al. Joint optimization of logistics infrastructure investments and subsidies in a regional logistics network with CO2emission reduction targets[J]. Transportation Research Part D: Transport and Environment, 2016, 32(4): 25−40.
[6] TANG J, TANG L, WANG X. Solution method for the location planning problem of logistics park with variable capacity[J].Computers&OperationsResearch,2013,40(1): 406−417.
[7] 蔚欣欣, 李悦, 陆化普. 基于实物期权的离散交通网络设计模型[J]. 公路交通科技, 2013, 30(7): 126−132.WEI Xinxin, LI Yue, LU Huapu. A model for discrete traffic network design based on real option[J]. Journal of Highway and Transportation Research and Development,2013, 30(7): 126−132.
[8] Dixit A P R. Investment under uncertainty[M]. Princeton:Princeton University Press, 1994.
[9] LI Z, GUO Q, Lam W H K, et al. Transit technology investment and selection under urban population volatility: A real option perspective[J]. Transportation Research Part B: Methodological, 2015, 78(1): 318−340.
[10] Chow J Y J, Regan A C. Network-based real option models[J].TransportationResearchPartB:Methodological, 2011, 45(4): 682−695.
[11] Chow J Y J, Regan A C, Ranaiefar F, et al. A network option portfolio management framework for adaptive transportation planning[J]. Transportation Research Part A: Policy and Practice, 2011, 45(8): 765−778.
[12] LI Z, Lam W H K, Wong S C, et al. Environmentally sustainable toll design for congested road networks with uncertain demand[J]. International Journal of Sustainable Transport, 2012, 6(3): 127−155.
[13] LI Z C, Lam W, Wong S C. Optimization of number of operators and allocation of new lines in an oligopolistic transit market[J]. Networks & Spatial Economics,2012, 12(1): 1−20.
[14] LI Z C L W. On the allocation of new lines in a competitive transit network with uncertain demand and scale economies[J]. Journal of Advanced Transportation,2011, 45(4): 233−251.
[15] Bajeux-Besnainou I, Joshi S, Vonortas N. Uncertainty,networks and real options[J]. Journal of Economic Behavior & Organization, 2010, 75(3): 523−541.

