基于粗糙集与熵的铁路货物周转量预测
杨丽蓉,吕红霞
(1. 西南交通大学 交通运输与物流学院,四川 成都 610031;2. 全国铁路列车运行图编制研发培训中心,四川 成都 610031;3. 综合交通运输智能化国家地方联合工程实验室,四川 成都 610031)
铁路货物运输是我国货物运输的重要运输方式 ,凭借其运输量大、安全性高、运价极低的优势,成为我国运输市场的主力,尤其是对于长距离运输的大宗货物其优势明显。近年来,我国铁路货物运输量在国家大力支持的背景下,由于其他各种运输方式的冲击,仍出现较为明显的下降。结合历史运营状况,消除冗余因素的影响,进行货物运输市场的科学预测。对合理制定运输计划具有重要的指导意义。近年来,张诚等[1]运用粗糙集对铁路货物周转量预测进行了研究,秦俭等[2−4]运用粗糙集研究了物流需求预测。最常见的粗糙集离散化方法是等距离划分或者等频率划分。等距离划分需要使用者首先给定一个不小于二的整数,然后根据各条件属性的实际值或增减率,将属性的值域划分为几个离散的区间;等频率划分则需要规定每个区间的样本数,然后再进行离散。上述研究为离散化预测奠定了一定的理论基础,但是几乎没有考虑决策表内各样本间的不可分辨关系,离散后的结果可能会改变系统内的不可分辨关系[5],继而改变条件属性与决策属性间的关系,使预测结果产生偏差。运用基于粗糙集的简单熵离散化方法,在保持属性间的关系的前提下离散数据,得出影响货物周转量的核心因素。借助Eviews软件拟合并检验参数可靠性,运行模型,得到货物周转量及其增长趋势。
1 粗糙集理论与预测方法
粗糙集是用来解决对象信息不精确、不完整等问题的一种数学工具,由波兰学者Pawlak提出[6]。利用粗糙集,可以将无法描述或隐含的知识挖掘出来,以表达信息系统的内容,找出决策系统潜在的规律,为决策提供判断依据。
1.1 粗糙集基本知识
在信息系统中,条件属性与决策属性之间存在着某种不分明关系,称之为不可分辨关系。设论域为U,S为论域U上的一个等价关系簇。假如PS⊆,P≠∅,则P中所有等价关系的交集仍是论域U的一个等价关系[8]。称为P上的不可分明关系,记作IND()P。

在确定不同的属性重要性时,可以利用属性依赖度来确定指标的权重,此处需要用到关于粗糙集正域的理论。设近似空间为(U, R),XU⊆。

定义信息系统S中决策属性D以依赖度K(0≤K≤1)依赖于条件属性C,令,PQR∈,当且仅当其中r表示属性依赖度,Card()U 表示集合U的基数,即U中的元素个数[10−11]。
1.2 基于粗糙集与简单熵的组合预测方法
1.2.1数据处理
选取近几年GDP、第一产业增加值、第二产业增加值等数据为原始数据,计算以上数据的增长率,后期离散化处理、重要度计算均在增长率方面进行。选择增长率进行分析相比于分析单一的数据可以获得更准确的信息。
计算出增长率之后,运用简单熵的方法得出可以供粗糙集分析使用的离散化数据。接下来对简单熵离散化数据的计算进行简单的介绍。
熵来源于热力学,表示不能做功的热能[12]。常见的简单的连续数据离散化的方法有等宽法、等频法和 K-means算法,都属于非监督的离散化方法[13]。等宽法离散数据时使每个区间宽度均为K,该方法离散后的结果极为脆弱;等频法离散化数据时,将最大的区间划分为K个,使每个区间具有m/K个值,忽略了样本的原本分布信息;K-means算法作为聚类分析应用较为成功的方法,在数据离散化问题上尚缺乏理论依据。这 3种方法均为非监督离散化,采用基于简单熵的监督离散化方法,可以以极大的区间纯度确定离散时的分割点。
定义第i个区间的熵ei如下:

式中:pij为表示第i个区间中第j类属性值的比例;K为完整区间内样本值的类别数。

将属性划分为目标n个区间以后,从0开始,采用从小到大的整数对不同的样本进行编码,同一区间的样本编为同一个码。对属性集中每个属性编码以后便可得到离散化后的决策系统。
1.2.2依赖度之差
在筛选属性时,以前的研究学者常用的方法是通过比较单一属性的依赖度来确定属性的重要性,但决策属性对多个单一条件属性或条件属性的依赖度可能会相同[14],属性的重要度便无法确定,此时,可以借助单一属性或属性集的依赖度之差来比较。
进行属性依赖度之差求解时,首先对决策系统按决策属性D进行划分,具有相同离散值的样本化为同一类;然后计算决策属性D分别对条件属性集C与属性集C′的依赖度;最后,利用定义的属性依赖度之差计算各单一属性的依赖度之差,确定出属性重要度。
1.2.3预测方法
采用的预测方法为多元线性回归预测法[16]。对于文中这样的实际问题,有多个样本,可以设被解释变量 yi与解释变量 xi1,xi2,…,xin的线性规划模型为

参数估计完毕以后,需要对模型进行回归系数显著性的t检验和回归方程显著性的F检验[17]。
2 铁路货运数据离散及变量选取
通过对以往常见方法的研究,期望以铁路货物运输为例,寻找一种更新、更直观的预测方法。通过对影响货物周转量的因素进行分析,选取合理的因素作为自变量,以粗糙集为基础,对于决策系统中的属性值进行离散,得出决策表,计算得出重要的自变量,最后根据因素分析的结果进行回归分析预测。
2.1 预测指标体系
随着市场经济发展趋于成熟,影响货物周转量的因素众多,其中经济因素作用明显。因此,选取的有GDP、第一产业增加值、第二产业增加值、第三产业增加值、社会消费品零售总额、居民消费水平、进出口总额[2]。同时,选择能够反应货物运输效率的铁路货物周转量作为因变量,货物周转量是用货物吨数乘以运输距离得来的,是运输量与运输距离的复合指标。
2.2 原始数据及其处理
选取2002年至2012年的数据作为原始数据,见表1。

表1 2002~2012年属性原始数据Table 1 Attributes raw data from 2002 to 2012
对原始数据进行处理,求出GDP,进出口总额和货物周转量等的增长率,得出初始的信息系统。相对于原始数据,增长率具备较佳的信息表述能力。增长率计算结果见表2。
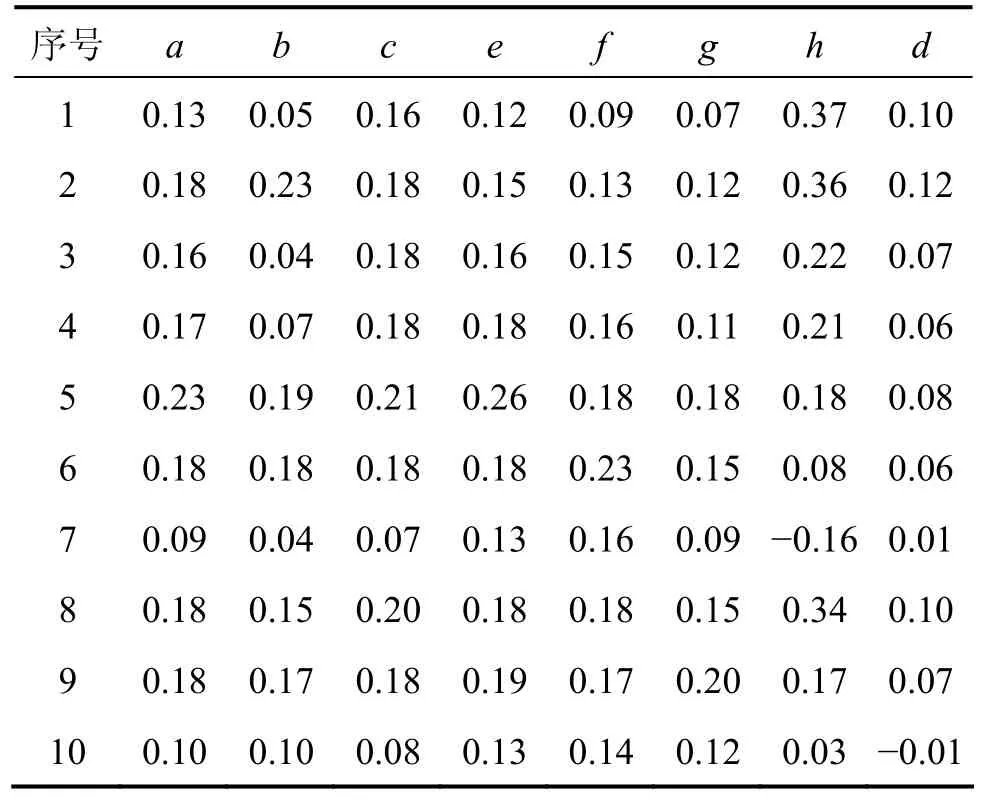
表2 属性增长率Table 2 Growth rate of attributes
按照简单熵离散化方法计对初始信息系统进行离散化处理,得出离散化后的决策系统,离散化最终结果见表3。
2.3 属性重要度计算
对增长率离散化以后,可以依据粗糙集等价理论将初始信息系统决策表按照不同属性分类,获取不同属性的依赖度之差,即单一属性重要度。下面以h属性为例,对计算过程进行展示。

表3 离散化决策信息系统Table 3 Discrete decision information system
1) 对决策属性集D进行等价划分:

2) 对除开属性 h后的条件属性集进行等价划分:
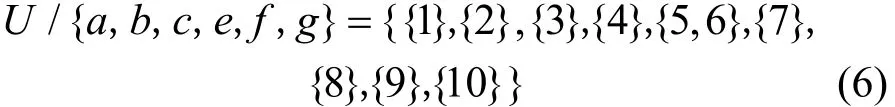
3) 决策属性等价集与条件属性等价集的交集:
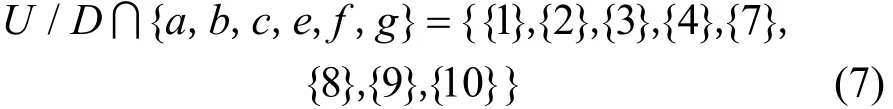
4) 决策属性集D对条件属性集{a,b,c,e,f,g}的依赖度与依赖度之差:
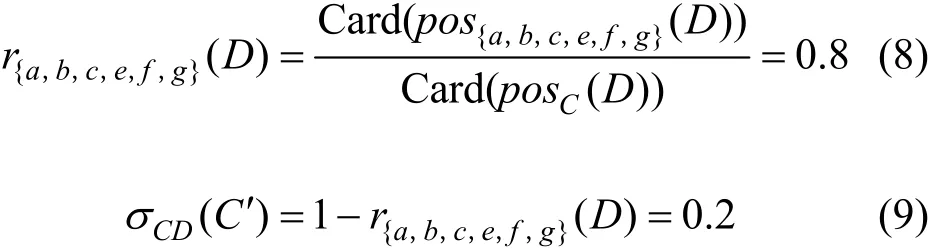
同理,用同样的方法求得其他单一属性的依赖度之差,见表4。
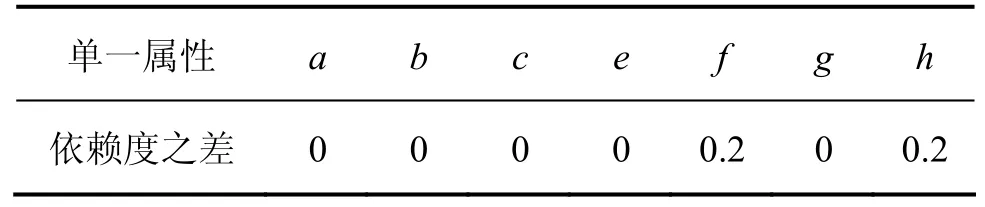
表4 单一属性依赖度之差Table 4 Difference of single attribute dependence
由表4可知,依据属性依赖度之差判断,决策属性d对条件属性f与条件属性h存在依赖,2个属性条件可作为预测的重要属性。因此,选取社会消费品零售总额与进出口总额作为预测的自变量。
3 周转量多元回归预测
3.1 建立回归模型
由前面的分析可知,社会消费品零售总额与进出口总额对货物运输周转量影响较大,且二者对其重要性相同。因此,将选取社会消费品零售总额与进出总额的增长率作为解释变量,货物运输周转量的增长率将作为被解释变量。令自变量社会消费品零售总额增长率、进出总额的增长率分别为 X5和X7,因变量货物运输周转量的增长率为Y。
利用多元线性回归模型来对货物周转量进行需求预测,设定模型为:

式中:ci表示常数;bij第i个样本的第j个自变量的系数。
3.2 参数估计与预测
3.2.1参数估计
计算过程采用 Eviews进行参数的估计,此处引入 AR(1)变量以消除变量间的一阶自相关关系[18−19]。计算结果如下:
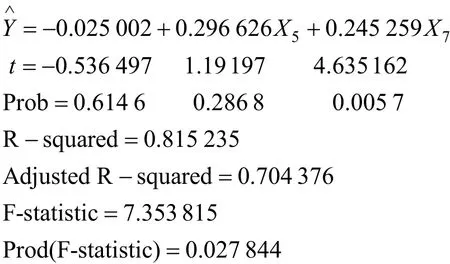
通过上述结果可知,检验结果表明判决系数为0.815 235,修正判决系数为0.704 376,比较接近于1,模型对样本的拟合度较好。t检验达到了理想水平,并且,F检验的P值为0.027 844,远小于0.05,模型在α=0.05的水平上显著置信区间达到0.95,模型通过了检验。
3.2.2预测
根据统计年鉴可知2013年至2015年的社会消费品总额增长率、进出口总额增长率,见表5。

表5 2013年~2015年相关增长率Table 5 Relative growth rate from 2013 to 2015
由模型可得2013年至2015年货物周转量的增长率,结合2012年货物周转量29 187.09亿t·km,得2013年至2015年货物周转量。预测结果见表6。

表6 2013年~2015年预测结果Table 6 Forecast results from 2013 to 2015
由预测结果可知按照当前的运营模式发展,铁路的货物周转量有可能呈低走趋势,这给运营管理人员提出一个警示,对此预测结果,可以进行详细的分析,找出目前的运营存在的问题,针对问题做出一些调整,使周转量在将来能够呈稳步增长态势。
4 结论
1) 由预测模型可得 2013年,2014年和 2015年货物周转量的增长率分别为1.9%,1.0%和−3.8%,货物周转量分别为29 746.26,30 054.87和29 812.16亿 t·km,与实际数据相对吻合度分别为 98.04%,90.83%和78.29%,平均为89.05%。通过对货物周转量的预测可知,铁路货物周转量有下降趋势,这与近两年研究者对铁路货运的研究一致。
2) 该模型的建立基于改进后的粗糙集离散化方法,相对其他方法而言,在重要变量选取的过程中,离散化保留了变量间的分辨关系,结果更可靠,对我国货物运输计划具有一定的参考价值。
3) 若对预测模型再进行改进,可以得出接近实际数据的预测结果。以基于粗糙集的货物周转量重要变量选取问题为重点,预测年限越近时预测的准确率越高,后期可进一步探讨重要变量选取与其他预测方法结合的可能性,扩大预测年限。
参考文献:
[1] 张诚, 张广胜. 基于粗糙集理论的铁路货运需求预测研究[J]. 科技管理研究, 2012, 32(17): 212− 215.ZHANG Cheng, ZHANG Guangsheng. Demand forecast of rail freight based on rough set theory[J]. Science and Technology Management Research, 2012, 32(17): 212−215.
[2] 秦俭. 基于粗糙集与多元回归的我国物流需求预测[J].物流技术, 2014, 33(13): 298−299, 311.QIN Jian. Forecasting of Chinese logistics demand based on rough set theory and multiple regression[J]. Logistics Technology, 2014, 33(13): 298−299, 311.
[3] 冯怡, 张志勇, 徐广姝, 等. 基于粗糙集理论的我国物流需求预测[J]. 物流技术, 2010, 29(1): 60−62.FENG Yi, ZHANG Zhiyong, XU Guangshu, et al. The forecasting of logistics demand in China based on rough set theory[J]. Logistics Technology, 2010, 29(1): 60−62.
[4] 钟映竑, 黄鑫. 基于粗糙集和支持向量机理论的物流需求预测研究[J]. 工业工程, 2015, 18(2): 28−33.ZHONG Yinghong, HUANG Xin. Study on the logistical forecasting method based on rough set theory and support vector machine (SVM)[J]. Industrial Engineering Journal,2015, 18(2): 28−33.
[5] 陈东升. 保持不可分辨关系的离散化方法[J]. 郑州轻工业学院学报(自然科学版), 2007, 22(1): 87−91.CHEN Dongsheng. Discretization method based on indiscernibility[J]. Journal of Zhengzhou University of light industry (Natural Science), 2007, 22(1): 87−91.
[6] 李秀竹. 粗糙集理论及其在管理决策中的应用浅析[J].信息技术, 2007, 31(7): 141−142.LI Xiuzhu. Analyses of rough set theory and the application in management decision[J]. Information Technology, 2007, 31(7): 141−142.
[7] 王国胤. Rought集理论与知识获取[M]. 西安: 西安交通大学出版社, 2001: 18.WANG Guoyin. Rought set theory and knowledge acquisition[M]. Xi’an: Xi’an Jiaotong University Press,2001: 18.
[8] 苗夺谦, 李道国. 粗糙集理论、算法与应用[M]. 北京:清华大学出版社, 2008: 25−26.MIAO Duoqian, LI Daoguo. Rough sets theory algorithms and apllications[M]. Beijing: Tsinghua University Press, 2008: 25−26.
[9] ZENG Anping, LI Tianrui, ZHANG Junbo, et al. An incremental approach for updating approximations of rough fuzzy sets under the variation of the object set[C]//Rough Sets and Current Trends in Computing, 2012:36−45.
[10] Pawlak Z. Rough set[J]. International Journal of Computer Information Science, 1982, 11(5): 341−350.
[11] Pawlak Z. Rough set theory and its applications to data analysis[J]. Cyberneties and System, 1998, 29(7): 661−668.
[12] Gray, Robert M. Entropy and information theory[M].Beijing: Science Press, 2012.
[13] 阙夏. 连续属性离散化方法研究[D]. 合肥: 合肥工业大学, 2006: 15−23.QUE Xia. Study on the discrtization of continuous attributes[D]. Hefei: Hefei University of Technology,2006: 15−23.
[14] 王小菊, 蒋芸, 李永华. 基于依赖度之差的属性重要性评分[J]. 计算机技术与发展, 2009, 19(1): 67−70.WANG Xiaoju, JIANG Yun, LI Yonghua. Significance of attribute evaluation based on dependable difference[J].Computer Technology and Development, 2009, 19(1):67−70.
[15] 刘凌霞. 基于粗糙集理论属性重要性的离散化算法[J].广西轻工业, 2007, 23(10): 75−76.LIU Lingxia. Discretization algorithm based on attribute importance of rough set theory[J]. Guangxi Journal of Light Industry, 2007, 23(10): 75−76.
[16] Chatterjee Samprit, Hadi Ali S. Regression analysis by example[M]. Hoboken, N J: Wiley, 2012.
[17] Kleinbaum, David G. Applied regression analysis and other multivariable methods[M]. 3rd ed. Beijing: China Machine Press, 2003.
[18] 刘巍, 陈昭. 计量经济学软件: Eviews操作简明教程[M]. 2版. 广州: 暨南大学出版社, 2013.LIU Wei, CHEN Zhao. Econometrics software: a concise guide to Eviews operations[M]. 2nd ed. Guangzhou:Jinan University Press, 2013.
[19] I Gusti Ngurah Agung. Cross section and experimental data analysis using Eviews[M]. Singapore: John Wiley &Sons, 2011.

