航天器三维空间追逃问题研究
刘 源, 李玉玲, 郝 勇, 周俊峰
(哈尔滨工程大学自动化学院, 黑龙江 哈尔滨 150001)
0 引 言
本文应用协同进化算法解决两航天器的三维空间追逃问题,这是一个对抗双方的对策组合问题,此对策组合中存在纳什均衡。航天器追逃是一个复杂的过程,对抗双方需根据对方的实时信息进行自主决策,不断调整运动轨迹来实现逃避或追击。文献[1]通过目标视线法解决了一种航天器追逃问题,并通过线性反馈和一个二次目标方程,生成有效解决线性二次问题的最优反馈方法,但误差会随二次积分而累积。文献[2]采用一种半直接法的数值求解方法,通过此方法解决了共面轨道的追逃问题及三维空间两战斗机对抗问题,此方法求解得到的数值精度受近似初值的影响。微分对策在空间飞行器追逃问题的研究中应用广泛,对纳什均衡点的研究成为微分对策的热点研究方向。文献[3]基于微分对策理论研究了两航天器在固定时间下的追逃问题的最优控制策略及数值求解方法,但此方法需解24维非线性微分方程组,计算较复杂。
协同进化算法是基于协同进化论基础上提出的一种新的进化算法。协同进化思想基于博弈论的观点,采用相互对立的种群表示对抗双方,进化过程中种群之间互相交换信息,并根据对方种群提供的信息向最优化各自的支付函数方向进化。协同进化算法最早由Hillis[4]提出,算法以捕食—猎物协同进化关系为模型,使算法的智能搜索能力增强。文献[5]提出协同进化增广Lagrangian方法将对策双方的个体转换成近似零和矩阵后再求解鞍点。协同进化算法在生产制造、工业设计、目标识别和生命科学等领域应用广泛。近年来,协同进化算法在航空航天领域引起关注。文献[6]基于协同进化算法解决了卫星编队自主重构问题,并得出Pareto最优解的求解方法。文献[7]提出多中心合作协同进化规划算法,解决了“分治—合作”策略的多卫星中心协同规划问题。目前,采用协同进化算法解决空间追逃问题的研究较少,尚未得到广泛的应用。与传统遗传算法相比,协同近化算法具有较强的自主搜索能力和渐进学习能力,并且算法的鲁棒性强。由于协同进化算法的编码特性,其对控制量编码时得到的是离散型数据,因此,可采用B样条基函数对控制量进行拟合。B样条曲线是在贝塞尔曲线的基础上改进而来的,可以对多种形式的函数变量进行逼近,具有很好的通用性和简洁性。
本文研究在近地圆轨道附近的两航天器在连续小推力作用下的追逃问题,并且对抗双方的初始运动状态为已知,对抗时间固定。根据纳什均衡[8-10]理论的基本思想,以二者终端的相对距离作为支付条件,建立航天器在参考轨道中的动力学模型,利用协同进化算法规划出对抗双方的最佳追逃策略组合,为航天器追逃问题提供一种较为有效的解决方法。
1 问题描述
在追捕器和逃逸器附近的圆轨道上选取一动点,以该动点为坐标原点建立如图1所示的动坐标系。图1中O为参考坐标系原点,X轴在地心和O点的连线上,Y轴沿轨道运动方向,Z轴与X轴、Y轴构成右手系,P表示追捕器,E表示逃逸器。两航天器的空间位置如图1所示。

图1 航天器空间追逃参考坐标系
空间追逃问题是在严谨数学模型下的冲突对抗问题,属于博弈论范畴[11-13],其最优策略求解的关键在于纳什均衡点的计算。本文将求解三维空间中两航天器最优追逃策略问题转化为利用协同进化算法求解纳什均衡点[14-15]的问题。
2 数学模型的建立
在相对轨道参考坐标系中,航天器单位质量控制力ui在o-xy平面内的投影与x轴夹角为α(-π<α≤π),单位质量控制力ui与o-xy平面夹角为β(-π/2<β≤π/2),如图2所示。

图2 单位质量控制力在参考轨道中投影
那么航天器单位质量控制力ui在参考坐标系三轴分量为
(1)
式中,(fix,fiy,fiz)为航天器相对参考坐标系的单位质量轨道控制力在参考坐标系上的投影;i为P或E。由式(1)可知,通过调整俯仰控制角α和偏航控制角β,即可改变航天器三轴控制力,进而实现轨道机动。
在二体引力作用下,当追捕器和逃逸器运行在近似圆轨道,并且两航天器的相对距离相比参考轨道长半轴为小量时,两航天器在相对参考坐标系中的运动可由C-W方程描述[16],本文的研究对象符合C-W方程的适用条件。
(2)
式中,ω为参考轨道的平均轨道角速度;(xi,yi,zi)为航天器在参考轨道坐标系中位置分量。
将式(2)表示成状态空间表达式,即
(3)
式中
(4)
(5)
(7)
当航天器初始状态为已知时,式(3)的解析解为
(8)
其中
(9)
Φ(t,t0)为系统的状态转移矩阵,其具体形式[17]为
(10)
式中,τ=t-t0。当ui(t)为常数ui0时,可计算出
(11)
故式(8)可进一步表示为
xi(t)=Φ(t,t0)xi(t0)+Ψ(t,t0)ui0
(12)
由式(12)可知,若已知航天器初始状态xi(t0)及控制力ui0,即可求得航天器任意时刻在相对参考轨道的运动状态。

xis(tn)=Φ(tn,t0)xis(t0)+EUi+Ψ(tn,tn-1)uin
(13)
其中
(14)
(15)
利用追逃双方在参考轨道中的末段相对距离设计支付函数,即
(16)
3 协同进化算法空间追逃设计
协同进化算法求解空间追逃问题框架如图3所示。

图3 协同进化算法求解空间追逃问题框架
3.1 追逃策略设计
追逃双方以vi为输入信号,其中vi=[αi,βi]T,其中i为P或E。协同进化算法以α、β为编码对象。假设固定对策时间为Ts,那么在时间区间[T(k-1)/n,Tk/n](k=1,2,…,n)内对抗双方的输入信号为vik,其中,n为离散化步长,则两航天器的进化算法编码可表示为(vi1,vi2,…,vin)。采用随机生成方式产生追逃双方的初始种群分别为IP和IE,种群规模为N。
利用B样条基函数对控制量α、β进行逼近拟合。在[T(k-1)/n,Tk/n]控制量可描述为(Q+n)个B样条基函数在各时间区间上相加的形式,即
(17)
式中,ak表示基函数系数;Q表示基函数的阶次;Bk(t)是节点序列k的Q阶B样条基函数,则第k个P阶B样条基函数,可通过德布尔-考克斯迭代计算公式进行描述,即
(18)
利用B样条基函数将协同进化算法编码得到的离散量进行逼近拟合,得到对抗双方俯仰控制角α和偏航控制角β的时间历程,进而根据式(1)及式(13)得到对抗双方的相对位置。
3.2 共享适应度
两航天器在对抗过程中,可以通过星载的传感器获取自己的状态,可以利用地面雷达或高轨的卫星监测网及数据链来获得对方状态信息。本文的研究是假设对抗双方是理性的,会根据对方当前状态采取对其自身最有利的控制策略,然后参与博弈的成员最终会达到纳什均衡状态,理性对手的假设是博弈理论成立的基础。适应值共享[18-20]是维持种群多样性的有效方法,可实现在Pareto集合中实现均匀采样,避免算法落入局部最优。
设xej为逃逸种群中的个体j,xpw为追捕种群中的个体w,那么两个体的末段相对距离为
djw=d(xej,xpw)
(19)
定义共享函数为
(20)
式中,a为常数;σshare为小生境半径,由期望的个体之间最小分离程度估计出来。种群中个体j的小生境数sj由种群中全部个体的共享函数之和得到,即
(21)
那么逃逸种群中个体j的共享适应度为
(22)
追捕种群中个体k的共享适应度为
(23)
3.3 协同进化算子设计
3.3.1选择算子
选择算子采用具有随机采样特征的轮盘赌选择,其基本思想是根据每个个体适应值在种群中所占的比例来确定该个体被选中的概率,可确保每个个体都有生存下来的机会,避免算法出现早熟现象。
3.3.2协同交叉算子
种群中个体x=(x1,x2,…,xn)和个体y=(y1,y2,…,yn)的差异度为
(24)
式中,n为个体长度。那么当两个体的差异度D(x,y)>u时(u为[0,1]随机数),采用单点交叉方式产生新的个体。
当两个体的差异度D(x,y) 图4 两点交叉运算 3.3.3变异算子 变异算子采用有向变异方法,假设梯度方向由d近似表示,那么变异后的子代个体可为 x′=x+rd (25) 式中,r为非负随机数。近似梯度d的第m个元素计算方法为 (26) 式中,Δxm为小实数。采用有向变异方法增加种群多样性的同时,能够使种群中的个体朝有益方向进化,避免变异产生劣势个体,增强算法的收敛性。 3.3.4协作算子 (27) (28) IP和IE为两个独立进化的种群,在不同的决策空间进行搜索。通过协作算子,使两个种群可相互交换信息,根据对方提供的信息来决策本种群的进化方向,实现两个种群的协同进化。 为避免随机因素影响导致优势解丢失,在协同进化过程中采用精英保留机制,在每一代进化过程中,将父代中u个个体和此父代产生的子代中的λ个个体合并得到新的群体,并在此群体中挑选优势个体组成下一代父种群[21-22]。操作方法如图5所示。 图5 精英保留机制示意图 步骤1对追逃问题进行编码设计,产生追逃双方的初始种群。 步骤2计算种群中每个个体的共享适应度。 (1) 追捕种群的个体分别在逃逸种群中随机选取10个个体与之对抗,累计适应度; (2) 将追捕种群的个体按照适应值由大到小排序,选中10个最优个体。逃逸种群中的每个个体分别与选中的这10个追捕种群的最优个体对抗,累计适应。 算法采取此对抗方式,可减小算法计算冗余度,并且能够保证每个个体至少参与10次对抗,保留种群的多样性。 步骤3判断是否满足算法终止条件。若满足,则执行步骤5;否则执行步骤4。 步骤4分别对追、逃种群进行选择、交叉、变异、协同操作,得到新的种群。返回步骤2。 步骤5输出追、逃种群的最优个体。 步骤6解码计算,得到最优追逃策略。 算例1追逃双方初始位置在异面轨道情况下,追捕器和逃逸器的最大加速度分别为aP=0.017g和aE=0.013g,其中,g≈9.8×10-3km/s2,对策时间为900 s,仿真步长为10,算法进化代数为500,种群规模为250,交叉概率为0.5,变异概率为0.05。参考轨道参数如表1所示。对抗双方相对参考轨道的初始运动状态如表2所示。由协同进化算法得到的最优追逃路径如图6和图7所示。追逃双方加速度在参考轨道中三轴分量随步长变化关系如表3所示。 表1 参考轨道参数 表2 异面轨道追逃双方初始运动状态参数 图6 对抗时间为900 s时异面轨道两航天器最优追逃路径 图7 对抗时间为900 s时异面轨道追逃双方运动轨迹在 参考轨道随时间变化曲线 由图6和图7可知,本文采用的协同进化算法迭代收敛。当两航天器初始位置为异面轨道,对抗时间固定为900 s时,本文所采用的协同进化算法能够规划出两航天器的最优追逃路径,并且在追捕器具有相对优势时,最终能够捕捉逃逸器。 对策时间为500 s时,由协同进化算法得到的最优追逃路径如图8和图9所示。 表3 对抗时间为900 s时异面轨道追逃双方加速度在参考轨道中的三轴分量所占比例变化 图8 对抗时间为500 s时异面轨道两航天器最优追逃路径 图9 对抗时间为500 s时异面轨道追逃双方运动轨迹在参考 轨道随时间变化曲线 由图8和图9可知,当追踪器由于对抗时间不足,未能捕捉到逃逸器时,对抗双方随对抗时间变化仍呈现出追逃效果。 为研究追踪器相对优势大小对追逃效果的影响,在表2中其他参数不变的基础上将追踪器的初始相对速度缩小为(11.2,11.67,10.38)(单位m/s)在对策时间为900 s时,其最优追逃路径如图10和图11所示。对比图6和图7可知,在对策时间及初始边界条件相同的条件下,当追踪器的相对优势缩小时,追踪器将难以捕获逃逸器。 图10 对抗时间为900 s时异面轨道两航天器最优追逃路径 (追踪器的相对优势缩小) 图11 对抗时间为900 s时异面轨道追逃双方运动轨迹在参考轨道随时间变化曲线(追踪器的相对优势缩小) 算例2追逃双方初始位置在共面轨道时,追捕器和逃逸器的最大加速度分别为aP=0.023g和aE=0.015g,其中,g=9.8×10-3km/s2,对策时间为900 s,仿真步长为10,算法进化代数为500,种群规模为250,交叉概率为0.5,变异概率为0.05。参考轨道参数如表1所示。对抗双方相对参考轨道的初始运动状态如表4所示。由协同进化算法得到的最优追逃路径如图12和图13所示。追逃双方加速度在参考轨道中三轴分量所占比例随步长变化关系如表5所示。 表4 共面轨道追逃双方初始运动状态参数 表5 对抗时间为900 s时共面轨道追逃双方加速度在参考轨道中的三轴分量所占比例变化 图12 对抗时间为900 s时共面轨道两航天器最优追逃路径 图13 对抗时间为900 s时共面轨道追逃双方运动轨迹在 参考轨道随时间变化曲线 由图12和图13可见,算法在算例2的迭代仍然收敛,结果表明,对策在900 s时,追踪器能够捕获逃逸器。且追逃双方在Z轴上的轨迹一致,说明追逃双方在初始位置在共面轨道条件下最优追逃策略为发生在共面轨道。 对策时间为500,由协同进化算法得到的最优追逃路径如图14和图15所示。由图14和图15可知,追踪器由于对抗时间不足,未能捕捉到逃逸器,但对抗双方随对抗时间变化仍呈现出追逃效果,且追逃双方在Z轴上的轨迹一致,这与算例2结论一致。 图14 对抗时间为500 s时共面轨道两航天器最优追逃路径 图15 对抗时间为500 s时共面轨道追逃双方运动轨迹在 参考轨道随时间变化曲线 算例3基于算例1的边界条件,对抗时间为900 s时,采用微分对策方法解决航天器追逃问题得到的仿真结果如图16所示。对抗时间为500 s时,采用微分对策方法解决航天器追逃问题得到的仿真结果如图17所示。规划耗时如表6所示。 图17 对抗时间为500 s时共面轨道追逃双方运动轨迹在参考轨道随时间变化曲线(微分对策法) Table 6 Co-evolutionary and differential strategy time consuming s 当对抗时间足以使追踪器捕获逃逸器时,存在多种最优对抗策略。但对抗时间不足时,采用本文所提出的方法与采用微分对策方法得到的最优追逃轨迹趋势大致相同,证明本文算法搜索到的追逃策略为最优策略。 采用微分对策方法能够规划出航天器追逃路径,且在对抗时间相同的条件下,使用本文方法与微分对策方法,航天器所消耗的能量相同。但微分对策方法需求解24维非线性微分方程组,且对策模型中含有非线性时变项,计算较复杂。而本文所采用的协同进化算法结构简单,适应性强,可在本文所研究的内容基础上,面向多航天追逃的策略求解问题进行下一步研究。 基于协同进化算法及纳什均衡思想解决了一类航天器三维空间追逃问题。所提方法对于追逃双方初始位置为异面轨道或共面轨道均能规划出最优控制策略及相应的追逃轨迹,并得到两航天器在追逃过程中的三轴控制量。仿真算例还表明,两航天器的初始轨道为共面轨道时,追逃双方在追逃过程中的最优控制策略仍发生在共面轨道上。与微分对策方法相比,本文算法结构简单,规划耗时短,且具有较好的鲁棒性。 参考文献: [1] RAIVIO T, EHTAMO H. Visual aircraft identification as a pursuit-evasion game[J]. Journal of Guidance, 2000, 23(4):701-708. [2] LUO Y Z,LEI Y J,TANG G J.Optimal multi-objective nonlinear impulsive rendezvous[J].Journal of Guidance,Control,and Dynamics,2007,30(4):994-1002. [3] 张秋华, 孙松涛, 谌颖, 等. 时间固定两航天器追逃策略及数值求解[J]. 宇航学报, 2014,35(5):537-544. ZHANG Q H, SUN S T, CHEN Y, et al. Strategy and numerical solution of pursuit-evasion with fixed duration for two spacecraft[J]. Journal of Astronautics, 2014,35(5):537-544. [4] HORIE K, CONWAY B A. Optimal fighter pursuit-evasion maneuvers found via two-sided optimization[J].Journal of Guidance, 2006,29(1): 105-112. [5] TANK M J, SUN B C. Coevolutionary augmented Lagrangian methods for constrained optimization[J]. IEEE Trans.on Evolutionary Computation,2000,4(2):114-124. [6] CETIN B, BIKDASH M, HADASH F Y. Hybrid nixed-logical liner programming algorithm for collision-free optimal path planning[J].IET Control Theory and Applications, 2007,1(2):522-531. [7] GLUBOS A, CROWFORD J, LOHN J. A comparison of techniques for scheduling earth observing satellites[C]∥Proc.of the 16th Conference on Innovative Applications of Artificial Intelligence,2004:121-128. [8] RATNOO A, SHIMA T. Guidance strategies against defended aerial targets[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(4):1059-1064. [9] MATTHEW B, SIMON L, ELIZABETH A. Path planning for improved visibility using a probabilistic road map[J]. IEEE Trans.on Robotics, 2010, 26(1): 195-200. [10] PONTANI M, CONWAY B A. Numerical solution of the three-dimensional orbital pursuit-evasion game[J]. Journal of Guidance, 2009, 32(2):474-487. [11] GUTMAN S, GOLDAM O, RUBINSKY S. Guaranteed miss distance in guidance systems with bounded controls and bounded noise[J]. Journal of Guidance, Control, and Dynamics, 2012,35(3):816-823. [12] TAN K C, YANG Y J, GOH C K. Distributed cooperative coevolutionary algorithm for multiobjective optimization[J]. IEEE Trans.on Evolutionary Computation,2006,10(5):527-549. [13] LI Q H, YANG S D, RUAN Y L. Improving optimization for genetic algorithms based on level set[J]. Journal of Computer Research and Development, 2006,43(9):1624-1629. [14] SHIMA T. Optimal cooperative pursuit and evasion strategies against a homing missile[J]. Journal of Guidance, Control, and Dynamics, 2012,34(2): 414-424. [15] YOU S H, LEE Y H, LEE W J. Parameter estimations of a storm surge model using a genetic algorithm[J]. Natural Ha-zards, 2012,60(3):1157-1165. [16] 邓泓, 仲惟超, 孙兆伟, 等. 基于遗传算法的卫星攻击路径规划方法研究[J]. 宇航学报, 2008, 30,(4): 1587-1592. DENG H, ZHONG W C, SUN Z W, et al. Method research of satellite attacking path planning based on genetic algorithm[J]. Journal of Astronautics, 2008, 30(4): 1587-1592. [17] 何定银. 拦截卫星末段机动轨道规划研究[D]. 哈尔滨: 哈尔滨工业大学, 2013:13-17. HE D Y. Research on planning of terminal maneuver orbit for the intercepting satellite[D]. Harbin: Harbin Institute of Technology, 2013:13-17. [18] SONG X M, ZHAN C S, XIA J. Integration of a statistical emulator approach with the SCE-UA method for parameter optimization of a hydrological model[J]. Chinese Science Bulletin, 2012, 57(26):3397-3403. [19] LEUNG C S, LAM P M, SITU W C. A graphics processing unit accelerated genetic algorithm for affine invariant matching of broken contours[J]. Journal of Signal Processing Systems, 2012, 66(2):105-111. [20] SHAN H B, ZHOU S H, SUN Z H. Research on assembly sequence planning based on genetic simulated annealing algorithm and ant colony optimization algorithm[J]. Assembly Automation, 2009,29(3):249-256. [21] HILIS W D. Coevolving parasites improve simulated evolution as an optimization procedure[J]. Artificial Life II, 1992,43(5):313-324. [22] 徐定杰,刘明凯,沈峰,等.基于自适应遗传算法的DGPS整周模糊度快速解算[J].航空学报, 2013,34(2):371-377. XU D J, LIU M K, SHEN F, et al. Fast DGPS integer ambiguity resolution using adaptive genetic algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2013,34(2):371-377.
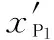



3.4 精英保留策略

3.5 协同进化算法具体流程
4 仿真较验



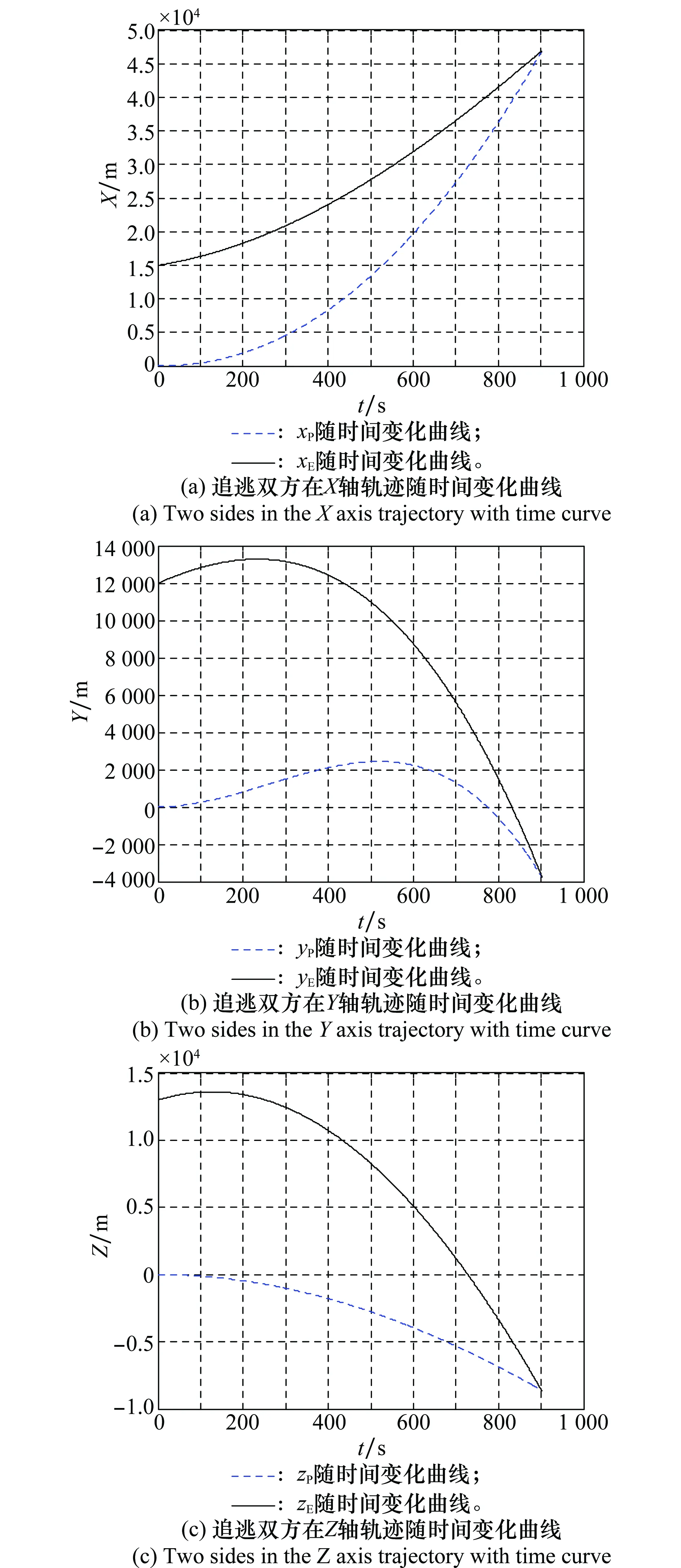





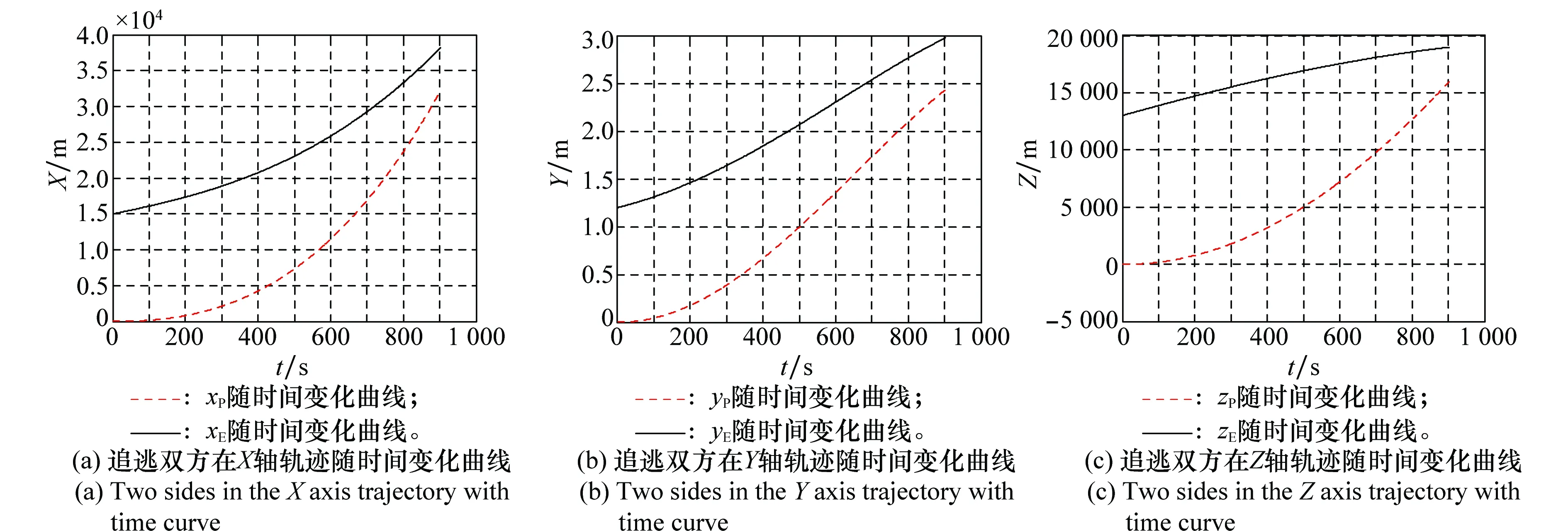









5 结 论

