基于压缩感知信号重构的间歇采样转发干扰对抗方法

原　慧, 王春阳, 安　磊, 李　欣

(1. 空军工程大学防空反导学院, 陕西 西安 710051; 2. 中国人民解放军94221部队, 山东 日照 276824)

0　引　言

目前,间歇采样转发干扰(interrupted-sampling repeater jamming, ISRJ)主要包括固定周期间歇采样直接转发干扰[1]、间歇采样重复转发干扰[2]、参差周期间歇采样干扰[3]、间歇采样逐次循环转发干扰[4]、间歇采样非均匀重复转发干扰[5]等,都是基于“存储-转发-存储-转发”干扰思想提出来的,以数字射频存储(digital radio frequency memory,DRFM)技术为实现基础,针对大时宽带宽积线性调频(linear frequency modulation, LFM)信号的新型灵巧干扰样式。ISRJ的特点主要体现在天线系统和信号采样存储阶段,即ISRJ既可用于收发系统隔离、同时工作的干扰设备,也可用于天线收发共用、分时工作的干扰设备,且无需对整段雷达脉冲信号进行无失真的全采样和存储。因此,ISRJ可以克服对收发天线同时工作带来的隔离度要求高、对宽带雷达信号的高速采样等难题,在弹载等干扰机平台较小的应用场合具有很大的实际应用价值。

ISRJ与文献[6]中提出的切片转发(chopping and interleaving, C&I)干扰相比,具有一定的相似性,但也存在本质区别:①对于收发共用天线,C&I干扰只能在下一个或几个雷达脉冲重复周期内完成干扰,而ISRJ可以在当前雷达脉冲重复周期内完成干扰;②C&I干扰信号在雷达的一个脉冲持续时间内是连续的,而ISRJ是间断的。由于ISRJ可以在当前雷达脉冲重复周期内完成干扰,因此,通过在脉冲重复周期间改变或调整发射信号或其参数的方法,例如相位扰动[6]、调频斜率调整[7]、脉冲分集[8-9]就失去了对抗效果。

理论上,可以通过在时频面内提取雷达信号和干扰的参数,实现目标参数提取和干扰抑制。但是,线性时频变换方法受限于不确定性原理,时频聚集性差,而非线性时频变换又存在交叉项问题,并且通常当干扰存在时,干扰的功率都强于雷达信号的功率,这就导致雷达信号在时频面被淹没。因此,对于较小的采样脉冲和较大的干扰信号比(jamming-to-signal ratio,JSR),通过在时频面内实现目标参数提取和干扰抑制是十分困难的。此外,由于干扰与目标回波信号的调频斜率相同,所以利用分数阶傅里叶变换(fractional Fourier transform,FRFT)进行扫频滤波[10]的方法也失效。文献[11]根据ISRJ信号的时域不连续性,以时频分析的方法检测只有回波信号存在的时间单元,根据回波单元所在的时频特性构建带通滤波器,从而实现对干扰的滤除,但是其并没有给出只有回波信号存在的时间单元长度的确定方法,并且在一定的干扰参数下,所构建的带通滤波器并不一定能将干扰完全滤除。

受此方法的启发,并结合压缩感知(compressed sensing,CS)信号重构思想,本文提出了一种新的ISRJ抑制方法。该方法同样利用ISRJ信号的时域不连续性,但不需要进行短时傅里叶变换等时频分析,只需要对雷达接收信号进行简单的能量函数运算,然后通过与设定的阈值比较,即可得到未受干扰影响的目标回波信号段;然后对提取到的未受干扰影响的目标回波信号段进行解线调处理,以保证解调后的信号在频域是稀疏的(线性调频信号经解调频后变为单频信号);最后,将提取到的未受干扰影响的目标回波信号看作是目标回波信号的压缩数据,根据其与目标回波信号稀疏频域之间的线性关系,建立CS最小问题求解模型并利用正交匹配追踪算法(orthogonal matching pursuit,OMP)重构目标信号,实现对ISRJ的抑制。

1　ISRJ信号特性分析

不失一般性,本文用间歇采样重复转发干扰的信号模型进行具体分析。图1给出了间歇采样重复转发干扰的原理示意图及其与目标回波信号的时频分布示意图,其中T和B分别为雷达发射LFM信号的脉宽和带宽;τ为采样切片的长度;Ts为切片采样周期;M重复转发当前采样信号的次数。

图1　间歇采样重复转发干扰原理示意图及其与目标回波信号的 时频分布示意图

由图1可以看出,干扰信号和雷达信号具有不同的时频变化特性,两者在任意时刻的瞬时频率都是不同的;此外ISRJ干扰是不连续的,即在干扰机的采样存储阶段不发射干扰信号。

雷达发射的幅度归一化LFM信号的数学模型可以表示为

(1)

(2)

ISRJ多用于突防环境下的自卫式密集假目标干扰,根据图1,雷达接收到的ISRJ信号可表示为

(3)

式中,τd表示干扰机的系统转发延迟。根据干扰方程可得干扰信号幅度Aj与干扰机的发射峰值功率、雷达天线主瓣增益、雷达发射信号波长以及干扰机与雷达的距离有关。

综合式(2)和式(3)可得雷达接收信号为

z(t)=sr(t)+sj(t)+n(t)

(4)

将信号s(t)的能量函数定义为其模值的平方,在一个脉冲持续时间内可以不考虑目标起伏的影响,即可以认为在一个脉冲持续时间内,目标回波信号的幅度是恒定的。那么,目标回波信号sr(t)、干扰信号sj(t)、以及不考虑噪声时干扰条件下的雷达接收信号x(t)=sr(t)+sj(t)的能量函数分别为

(5)

Ej(t)=|sj(t)|2=

(6)

(7)

式中

由于|cos[2πk(mτ+τd)t+φ]|≤1,所以在干扰转发时间段有(Aj-Ar)2≤Ex(t)≤(Aj+Ar)2。图2给出了目标回波信号、干扰信号以及不考虑噪声时干扰条件下的雷达接收信号的能量函数随时间的变化曲线。

图2　能量函数随时间的变化曲线

由图2可以看出,在间歇采样时间段,由于干扰机不发射干扰信号,雷达接收到的只有目标回波信号,信号能量平稳且较小,在干扰机发射干扰信号时间段,信号能量较大且起伏剧烈。

2　基于CS信号重构的抗ISRJ方法

2.1　目标回波信号压缩数据的提取

γ=mean(envminp(Ex(t)))

(8)

式中,envminp (Ex(t))表示取能量函数的极小值包络;mean(·)表示取均值。

因为

(9)

所以有

(10)

当噪声不可以忽略时,能量函数Ex(t)的包络不再是恒定的,而是有一定的起伏,且当干信比不是很大时,再利用上述方法求取的阈值来提取未受干扰影响的目标回波信号段时,可能会存在很大误差,即可能所得到的目标回波压缩数据并不“纯正”,很可能还包含有干扰信号数据。为了最大限度地去除干扰信号的影响,而又不损失太多有用的目标回波数据,受经验模态分解思想的启发,提出一种改进的提取未受干扰影响的目标回波信号段方法,具体步骤如下:

步骤1求雷达接收信号z(t)的能量函数Ez(t)的极大值包络envmaxp(Ez(t))和极小值包络envminp(Ez(t))。

步骤2求极大值包络和极小值包络的均值包络,得

(11)

显然envmoyp(Ez(t))相对于能量函数Ez(t)更加平滑,具有一定的抑制噪声影响能力。

步骤3取阈值为

γ=ρ×mean(envminp(Ez(t)))

(12)

式中,0<ρ≤1为阈值修正因子。因为干扰信号间歇采样的占空比小于等于50%且通常有Aj>2Ar,所以由式(8)得到的阈值偏大,加上噪声的影响,以此为阈值得到的信号中可能仍包含干扰信号。理论和仿真分析可得:在一定的信噪比(signal-to-noise ratio,SNR)和占空比条件下或在一定的SNR和JSR条件下,随着JSR或占空比的减小,ρ取逐渐减小的值可获得较纯净的目标回波信号数据;在一定的SNR条件下,大占空比和大JSR对提取未受干扰影响的目标回波信号数据都是有利的条件,此时可以取ρ=1。

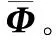
(13)

2.2　基于CS的目标回波信号重构

(14)

(15)

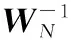
图3　基于CS信号重构的抗ISRJ干扰方法流程图

3　仿真与分析

3.1　对中带信号的仿真分析

雷达发射带宽B=10 MHz,脉冲宽度T=32 μs的LFM信号,采样频率fs=20 MHz,则采样点数N=640。假设间歇采样重复转发干扰的采样周期Ts=4 μs,不考虑干扰机的系统转发延迟,即τd=0。根据文献[13]的分析和式(16),当τ取不同值时可以形成以下4种主要的干扰效果:①Ts和τ满足式(16)所示关系时,所产生的假目标都是独立的;②Ts不满足式(16),并且τ不为Δt(Δt=T/(TsB)=0.8 μs为各主假目标间的分布间距)的整数倍时,主假目标群和非主假目标群将可能发生混叠,使其中有的假目标幅度呈现起伏变化;③Ts不满足式(16),但τ为Δt的整数倍时,由于相邻几次转发的主次假目标间相互重叠,假目标幅度不再是起伏的;④当Ts和τ不满足式(16)时,假目标之间发生相互混叠而出现了多个分布假目标,而且主假目标形成的分布假目标幅度最高。

(16)

式中,T、Ts、τ的单位均为μs;B的单位为MHz。

因此,根据分析,选取τ=2 μs、1.2 μs、0.8 μs、0.1 μs分别对应4种情况进行仿真分析。仿真中,定义干扰抑制前,即输入SNR和输入JSR的计算公式分别为

(17)

表1　τ=2 μs时本文方法的成功抗干扰概率Panti

表2　τ=1.2 μs时本文方法的成功抗干扰概率Panti

表3　τ=0.8 μs时本文方法的成功抗干扰概率Panti

表4　τ=0.1 μs时本文方法的成功抗干扰概率Panti

此外,为了与文献[14]提出的带通滤波方法(简记为BF,本文所提方法简记为CS)进行比较,定义干扰抑制后输出信号的信干噪比(signal-to-jamming-and-noise ratio,SJNR)为

(18)

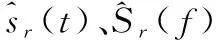
图4～图7分别给出了τ分别为2 μs、1.2 μs、0.8 μs、0.1 μs,对应的JSR分别为5 dB、10 dB、15 dB、20 dB,ρ分别取0.9、0.7、0.5、1时,干扰抑制前的相关处理结果、与BF方法相比的干扰抑制后的脉压结果以及CS信号重构效果。

图4　τ=2 μs时的仿真结果(JSR=5 dB,ρ=0.9)

图5　τ=1.2 μs时的仿真结果(JSR=10 dB,ρ=0.7)

图6　τ=0.8 μs时的仿真结果(JSR=15 dB,ρ=0.5)

图7　τ=0.1 μs时的仿真结果(JSR=20 dB,ρ=1)

由图4～图7可以看出,当τ不是非常小时,本文所提方法除了可以完全抑制干扰外,还基本可以相位不失真地重构目标回波信号;但当τ非常小(τ=0.1 μs)时,虽然仍然可以完全抑制干扰,但可能存在一定的相位失真。而BF方法不能完全抑制干扰,因为带通滤波器的带宽不能无限小,且带通滤波器的旁瓣可能非常高。

图8给出了τ分别为2 μs、1.2 μs、0.8 μs、0.1 μs时,BF方法和CS方法的干扰抑制性能曲线。其中,干扰抑制性能曲线的横坐标表示输入信号的信干比(signal-to-jamming ratio of input,SJR),显然,SJR=-JSR,纵坐标为SJNR,当输入SJR相同时,输出SJNR越大,表明干扰的抑制效果越好。干扰抑制性能曲线都是蒙特卡罗仿真100次的平均结果。

图8　中等带宽LFM信号条件下,不同τ值条件下的干扰抑制性能曲线

3.2　对宽带信号的仿真分析

宽带LFM信号是雷达实现高分辨率成像的一种常用信号。对这种宽带信号,首先进行去斜处理以显著降低系统的中频处理带宽[14]。文献[15]分析了ISRJ信号经雷达去斜处理后形成假目标的基本原理,研究了假目标的时域、频域、幅度、空间分布特性以及真假目标的空间分布关系,并指出:和针对利用匹配滤波处理技术的雷达的干扰相比,两者在形成假目标的幅度特性及各阶假目标之间的距离方面没有差别,从形成假目标的空间分布来看,两者存在较大差别,匹配滤波雷达中形成的主假目标必然滞后于真目标回波,而在去斜体制雷达中,可通过时延控制实现主假目标的超前干扰,且有多组时延参数可供选择。

此外,去斜处理不会影响能量函数的分布情况[16],因此也不会对未受干扰影响目标回波信号段的提取产生影响。

可以看出,理论上本文所提方法对去斜体制雷达对抗ISRJ依然有效。下面进行仿真验证。其中仿真参数如下:雷达发射LFM信号带宽B=1 000 MHz,脉冲宽度为T=128 μs,去斜处理后的中频带宽为10 MHz。假设目标为一单散射体目标,间歇采样重复转发干扰的采样周期Ts=10 μs,根据文献[16]的分析以及式(16),取3组τ和τd进行仿真(对应于式(16)的第4种情况要求τ<2 ns,这对干扰机要求较高,因此这里不考虑这一情况)。①τ=5 μs,τd=2.8 μs;②τ=2 μs,τd=1.7 μs;③τ=0.256 μs,τd=1.5 μs。

τ=5 μs、τ=2 μs和τ=0.256 μs对应的干扰转发占空比分别为50%,20%和2.56%,与第3.1节中的τ=2 μs、τ=0.8 μs和τ=0.1 μs对应的干扰转发占空比(分别为50%,20%和2.5%)相同或相近,因此宽带条件下,以上3种τ值条件下,不同JSR和阈值修正因子ρ条件下,本文所提方法的成功抗干扰概率也类似于表1、表3和表4,在此不再重复给出。图9给出了宽带条件下,τ分别取5 μs、2 μs和0.256 μs时,BF方法和CS方法的干扰抑制性能曲线。

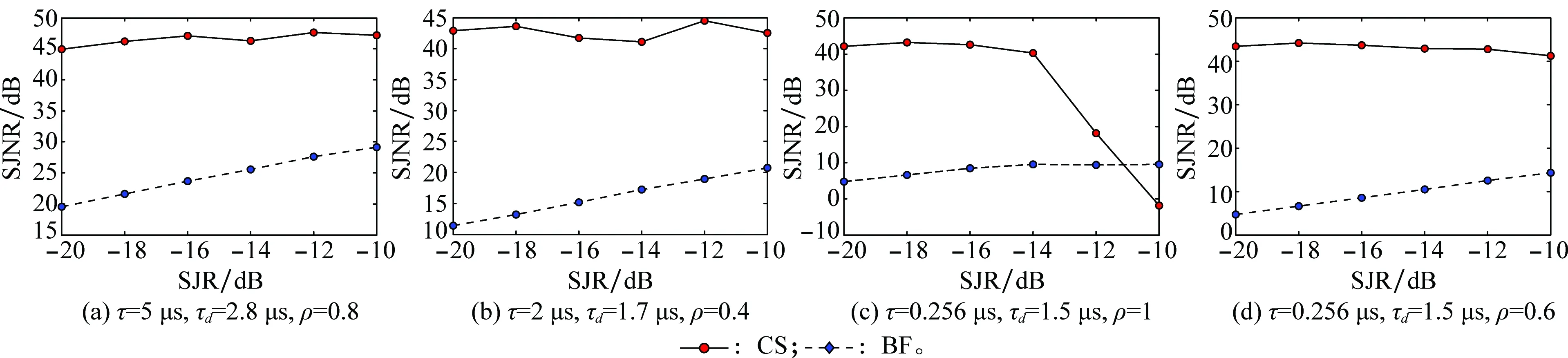
图9　宽带LFM信号条件下,不同τ值的干扰抑制性能曲线

由图9可以看出,对于宽带LFM去斜体制雷达,在适当的阈值修正因子条件下,CS方法的干扰抑制性能都基本能达到40 dB以上,远优于BF方法,说明CS方法也适用于宽带LFM去斜体制雷达对抗ISRJ。

4　结　论

本文利用间歇采样转发干扰信号时域的不连续特性,通过分析干扰与目标回波信号的能量函数特征,提出了一种有效可行地提取未受干扰影响的目标回波信号段的方法,经过解线调处理后作为压缩数据,利用解线调后的目标回波信号频域上的稀疏性,构建其之间的线性关系,得到CS最小问题求解模型,通过OMP算法实现了对目标回波信号的重构和对ISRJ干扰的抑制。仿真结果表明,通过设置合适的阈值,本文所提方法不仅适用于中带LFM匹配滤波雷达对抗ISRJ,而且适用于宽带LFM去斜体制雷达对抗ISRJ。而且,相比于文献[14]的方法,本文所提方法不仅提出了有效可行的未受干扰影响的目标回波信号段提取方法,而且干扰抑制性能也更好。

参考文献：

[1] WANG X S, LIU J C, ZHANG W M, et al. Mathematics principles of interrupted-sampling repeater jamming[J]. Science in China Series F: Information Sciences, 2006, 50(1): 113-123.

[2] 刘忠,王雪松,刘建成,等.基于数字射频存储器的间歇采样重复转发干扰[J].兵工学报,2008, 29 (4): 405-410.

LIU Z, WANG X S, LIU J C, et al. Jamming technique of interrupted-sampling and periodic repeater based on digital radio frequency memory[J].Acta Armamentarii,2008,29(4):405-410.

[3] 周政,唐宏,张永顺,等.基于时域采样的灵巧噪声干扰研究[J].现代雷达,2010,32(5): 53-55.

ZHOU Z, TANG H, ZHANG Y S, et al. A study on smart noise jamming based on time domain sampling[J]. Modern Radar, 2010, 32(5): 53-55.

[4] 刘建成,王雪松,刘忠.对线性调频脉压雷达的导前假目标群干扰[J].电子与信息学报,2008, 30(6):1350-1353.

LIU J C, WANG X S, LIU Z. Preceded false target groups jamming against LFM pulse compression radars[J]. Journal of Electronic and Information Technology,2008,30(6):1350-1353.

[5] 张养瑞,李云杰,李曼玲,等.间歇采样非均匀重复转发实现多假目标压制干扰[J].电子学报, 2016, 44(1): 46-53.

ZHANG Y R, LI Y J, LI M L, et al. Suppress jamming technique of multiple false targets on interrupted-sampling and non-uniform periodic repeater[J].Acta Electronica Sinica,2016,44(1):46-53.

[6] SOUMEKH M. SAR-ECCM using phase-perturbed LFM chirp signals and DRFM repeat jammer penalization[J]. IEEE Trans.on Aerospace and Electronic Systems, 2006, 42(1): 191-205.

[7] 冯祥芝,许小剑.随机线性调频斜率SAR抗欺骗干扰方法研究[J].系统工程与电子技术,2009, 31(1): 69-73.

FENG X Z, XU X J. Study of countermeasures to deceptive jamming using random linear modulation frequency ratio SAR[J]. Systems Engineering and Electronics, 2009, 31(1): 69-73.

[8] AKHTAR J. An ECCM signaling approach for deep fading of jamming reflectors[C]∥Proc.of the IET International Conference on Radar Systems, 2007:1-5.

[9] SCHUERGER J, GARMATYUK D. Performance of random OFDM radar signals in deception jamming scenarios[C]∥Proc.of the IEEE Radar Conference, 2009:1-6.

[10] SUN M H, TANG B. Suppression of smeared spectrum ECM signal[J]. Journal of the Chinese Institute of Engineers, 2009, 32(3): 407-413.

[11] GONG S X, WEI X Z, LI X. ECCM scheme against interrupted sampling repeater jammer based on time-frequency analysis[J]. Journal of Systerms Engineering and Electronics, 2014, 25(6): 996-1003.

[12] TROPP J, GILBERT A. Signal recovery from random measurement via orthogonal matching pursuit[J]. Transactions on Information Theory, 2007, 53(12):4655-4666.

[13] 王雪松,肖顺平,冯德军,等.现代雷达电子战系统建模与仿真[M]. 北京:电子工业出版社, 2010: 167-169.

WANG X S, XIAO S P, FENG D J, et al. Modeling and simulation of modern radar and electronic warfare systems[M]. Beijing: Publishing House of Electronics Industry, 2010: 167-169.

[14] WILLAM J C. Strech: a time-transformation technique[J].IEEE Trans.on Aerospace and Electronic Systems,1971,7(2): 269-278.

[15] 冯德军, 陶华敏, 杨勇, 等.对去斜体制雷达的间歇采样转发干扰[J]. 中国科学:信息科学,2012,42(2): 184-193.

FENG D J, TAO H M, YANG Y, et al. Jamming de-chirping radar using interrupted-sampling repeater[J]. Science in China: Information Sciences, 2012, 42(2): 184-193.

[16] YUAN H, WANG C Y, AN L, et al. A method against interrupted-sampling repeater jamming based on energy function detection and band-pass filtering[J]. International Journal of Antennas and Propagation, 2017, 2017 (1): 1-9.