基于图像分割的高频雷达射频干扰提取算法

罗忠涛, 吴太锋, 何子述, 陈绪元

(1. 重庆邮电大学通信与信息工程学院, 重庆 400065; 2. 电子科技大学电子工程学院, 四川 成都 611731; 3. 南京电子技术研究所, 江苏 南京 210013)

0　引　言

高频雷达工作于高频段,其性能容易受到由其他设备发射的同频段射频干扰(radio frequency interference, RFI)的影响。强RFI信号被雷达接收并经信号处理后,会在距离-多普勒(range-Doppler, RD)图上形成直线,影响目标检测和海杂波谱探测[1],因此RFI抑制是高频雷达必须考虑的问题。

高频雷达的RFI问题在高频雷达研究中一直广受关注。人们提出了基于不同原理的多种抑制方法,例如空域波束形成[2-3]、RD谱子空间投影[4-7]。近年来,文献[8-10]提出基于信号时频域分析的信号分解和消除,文献[11-12]曾提出波形和滤波器设计方法。以上算法均采用实测数据验证了其有效性,其中大部分要求采用不含或少含海杂波作为训练数据。否则,要求将RFI与海杂波信号相区分,这对于算法在不同海杂波状况下的稳健性提出了很高要求。

实际上,在RD域中实现RFI与海杂波的区分是一个有效方法,而训练数据可通过在RD图中选取干扰区域再逆处理至时域恢复得到。该方法对于地波雷达容易运用,对于天波雷达则必须考虑海杂波因素[11]。目前,高频段海杂波谱特性的研究,尚不能对RD图中杂波进行准确建模[12]。高频海杂波谱特性复杂且随机性大,从信号处理的角度难以给出一个有效且稳健的RD图干扰检测和提取的方法。

针对于此,本文首次提出将干扰提取，由信号处理问题转化为图像分割问题。首先采用灰度转换函数将RD图转化为灰度图;然后利用LOG算子降低高灰度的海杂波影响;最后研究直线提取算法,准确检测RFI,定位干扰直线在RD图中的位置,从而提取出干扰区域和干扰数据。

1　问题描述

一般情况下,RFI在RD图上表现为平行于距离维的直线,海杂波则为零多普勒附近的带状区域[9]。图1是根据文献[9]天波雷达RD图,进行数据恢复和RFI模型而生成的RD图。当干扰靠近海杂波区域时,射频干扰直线会与强海杂波相接触甚至被淹没。当干扰带宽较宽时,干扰线会覆盖全图。这些RFI线不仅会影响目标检测,也会影响基于海杂波特性的海态探测。因此引入RFI检测与抑制技术对于高频雷达来说是必须的。

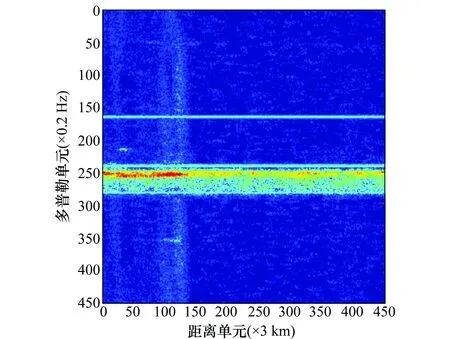
图1　天波高频雷达RD图

如前所述,高频雷达RFI已不乏研究。实际经验表明,传统基于空域或时频域的干扰抑制方法可以很有效,前提是训练数据包含所有干扰分量且不被掩盖。发射站静默情况下录取环境数据是可行的,但降低了雷达工作效率和训练数据的实时性。高频雷达一般采用当前帧数据,从中提取训练数据,但也因此容易受到海杂波的影响。

从雷达工作状态恢复训练数据,海杂波是不可忽略的因素。尤其是在天波雷达中,由于大功率发射连续波,其RD图的每个距离单元均含有强大的海杂波。因此,基于训练数据的RFI抑制的关键点在于如何在海杂波影响下精确提取干扰数据。

根据海杂波形成原理可知,海杂波无法通过时域或频域清除,只能利用其多普勒特征进行抑制。因此,如果能基于RD图将海杂波区域予以区分,准确提取出RFI区域,那么就可以恢复出高质量的干扰数据,从而提高干扰抑制算法的性能。

分析一般的高频雷达的RD图,大致可分为3个区域:

(1) 海杂波区域,一般位于Bragg频率附近,为边缘不整齐的带状;

(2) 射频干扰区域,表现为平行距离维且遍布整个距离维的直线;

(3) 噪声区域,幅度比海杂波低很多且幅度分布差别较小。

传统方法划定海杂波区域是在RD图中取多倍Bragg频率以内区域,以外则认为含有潜在的射频干扰。显然,传统方法难以解决靠近海杂波区域的窄带RFI线。因此,有必要研究一种能够在RD图中检测海杂波附近的RFI线的方法。而这在信号处理领域是个难题,尽管人眼往往能直观分辨出海杂波附近的RFI直线。

针对该问题,本文提出采用图像分割技术,从RD图中准确提取与海杂波邻近的RFI区域,从而精确地恢复出干扰数据,支撑干扰抑制算法。在此过程中,需重点考虑一个情况,即干扰线在与强海杂波相接区域被覆盖的情形。

2　RFI检测与提取方法

RFI线可能存在于RD图的任何多普勒位置,临近海杂波区域的干扰线是检测方法设计的重点。尽管RD图中干扰线一般为直线,但海杂波区域形状不定,导致两个区域的边缘模糊,传统直线检测算法不能准确有效检测出干扰线所在位置。

本文设计的RFI区域的检测和提取方法,其基本思路是:将传统RD图转换为灰度图像,采用高斯-拉普拉斯(Laplacian of Gaussian, LOG)算子去海杂波,结合边缘检测算法,分段检测再整段确定干扰线位置,提取出干扰区域。该方法的流程框图如图2所示,下面对各步进行详细分析和具体介绍。

图2　RFI区域提取的流程框图

2.1　灰度图像转换

首先将RD图转化为灰度图,作为后续图像分割的对象。一般RD图采用dB单位来呈现,以便观察绝对幅度比海杂波小得多的噪声和目标。本文方法将雷达常规处理得到的RD图转化为RD灰度图,通过对数变换的灰度变换方法实现。

对数变换需设置合理的最小值,以控制原数据的动态范围。灰度变换函数可以表示为

Y(p,m)=c·ln(1+b|X(p,m)|)

(1)

式中,X∈CP×M为RD图对应矩阵;b和c分别控制动态范围和灰度级。

在RD灰度图中的干扰线检测可归为经典的直线检测问题,但采用传统直线检测方法,例如边缘检测算子与Hough变换结合,并不能理想地检测和定位，因此干扰线检测算法必须专门设计。

2.2　LOG算子去海杂波

采用LOG算法处理RD灰度图,能够淡化海杂波区域而突出干扰边缘线。LOG算子曾被用于数字图像中的噪点模糊与边缘锐化[13-15]。其中高斯平滑滤波器可以对原始灰度图像进行平滑滤波处理,拉普拉斯锐化滤波器可以使得平滑处理过后的直线与海杂波之间的边缘更加明显。

LOG算子去海杂波运算如下:首先,对灰度图像Y(p,m)进行高斯平滑滤波处理,即利用高斯平滑函数G(p,m)与Y(p,m)进行卷积得到平滑滤波后的图像H(p,m)为

(2)

式中，G(p,m)是高斯滤波函数，表示为

(3)

然后,由线性系统卷积运算性质可得

(4)

最后,计算得到LOG算子为

(5)

式中,参数σ为滤波器的标准差,可默认为0.5。

实践经验发现,LOG算子在滤波与锐化处理过程中对像素点求取平均阈值,可有效降低或消除图像中孤立噪点以及较小的噪声组织,同时保留灰度图像中的边缘信息。因此,其能够有效地去除区域内灰度渐变的海杂波。

2.3　干扰线边缘检测

从去杂波后图像中检测干扰,本文方法采用了经典边缘检测算子,舍弃传统Hough变换,转而根据干扰线特性分析,专门设计了“先检测子线段,再连接为整线段”的方法。

首先,采用Canny算子对去海杂波后的灰度图像H进行边缘检测,并对边缘检测后的灰度值二值化处理,凸显区域边缘界线。设Canny算子和二值化处理之后所得矩阵为D。

然后,基于D矩阵检测干扰直线所在位置。设置待检测干扰线段最小长度为m0。针对多普勒单元p、中心为k、宽度为m0线段灰度值的序列,计算其元素灰度值是否为1的比例,记录为

(6)

之后,设定阈值α∈[0,1],判断该线段是否可能为干扰边缘线之子线段,并将判定为干扰直线的线段灰度值全部设为1。同时对待检测区域上每一段的λ(p,k)和α进行比较,并重新赋值,即

(7)

至此,初步判断中心位于(p,k)、长度m0的子线段是否为干扰边缘。

最后,利用RFI线必贯穿所有多普勒单元的特点,对已判子线段进行再判断,以排除非干扰边缘的虚警。设定再判断的阈值为β∈[0,1],计算多普勒单元p的整个距离维上元素灰度值为1的比例,记录为

(8)

当γ(p)≥β,则确定此直线为干扰线边缘;否则认为是虚警,并舍弃。

2.4　干扰区域与数据提取

由已检测的干扰线边缘,可以快速且方便地提取干扰区域,进而恢复干扰数据。

可令干扰直线所确定的干扰区域为矩阵B,其元素值为1或0,分别表示干扰和非干扰。至此完成干扰区域的提取工作。

欲恢复干扰数据,可将矩阵B与常规处理的RD图元素值矩阵X对应元素相乘,得到矩阵

Z=B⊙X

(9)

矩阵Z即为RD图中干扰区域的数据。将Z进行逆多普勒和逆脉冲压缩处理,即可恢复出RFI的时域样本数据。

3　算法性能分析与应用示例

3.1　算法性能分析

基于图像分割技术的干扰提取算法步骤可总结为:

步骤1将接收时域数据进行脉冲压缩和多普勒处理,得到RD图X;

步骤2将RD图的幅度进行对数运算,转化为灰度图Y,使用LOG算子去海杂波得到灰度图H;

步骤3针对去海杂波后图像H,采用Canny算子计算梯度并二值化,得到二值化图像D；

步骤4通过两次判决(子线段初判和整线段再判),确定干扰边缘线所在的多普勒单元;

步骤5根据边缘得到干扰区域B,对应于RD频谱图中干扰数据为矩阵Z。

本文图像分割的对象是干扰线受海杂波影响下的图像(类似图1)。高频雷达中有两种情况会造成RD图遍布条纹,需抑制后再使用本文方法。第一种是接收数据含有瞬态干扰,可采用传统时域消除-内插的方法[1]。第二种是接收数据含有宽带RFI,可采用滤波器设计稳定抑制,其样本可取自于高多普勒区域。本文算法可直接用于处理雷达接收的时域数据,或经处理后的RD图。与高频雷达正常信号处理相比,该算法应用不需要额外知识。

前面介绍算法时处理对象是全RD图,实际上可以通过减少多普勒单元来缩小图像分割区域,从而降低运算量。考虑到海杂波只存在于低多普勒域,因此可取多倍(如20倍)Bragg频率区域内为待处理区域,检测和提取潜在的干扰线。在恢复训练数据时,将干扰线与高多普勒区域合并为潜在干扰区域,足以抑制所有多普勒域的干扰。实践验证表明,如此处理能大幅减小运算量,提高运算速度,达到实时处理要求。

3.2　算法应用示例

本文算法应用的一大优势在于,由于采用图像分割得到了精确的干扰数据,可以支撑基于传统思路的干扰抑制算法发挥出应有的性能且不受海杂波影响而降低性能。下面给出两个例子:

(1) RFI数据提取用于辅助波束形成。已有的波束形成算法,需要精确的干扰样本区域选取[2]。当高频雷达阵列数据可用时,可采用本文方法对常规波束形成的RD图进行干扰图像分割,提取其区域矩阵B。然后,对每个阵元处理的RD图,采用B提取其干扰数据Z。进而基于阵列的干扰数据,设计出抑制干扰来向的波束形成。

(2) RFI数据提取用于辅助滤波器设计。基于滤波器设计的RFI抑制方法不受空域限制,其思路是从RD图中恢复出时域干扰数据,从而辅助滤波设计,然后用于脉冲压缩阶段抑制干扰[12]。

下面介绍本文提出的RFI提取算法如何改进基于滤波器设计的RFI抑制方法。滤波器设计以抑制干扰方法的基本思路:从当前帧接收数据中恢复干扰数据,估计干扰协方差矩阵,进行相似度约束下的滤波器设计,再通过脉冲压缩处理来抑制RFI。

该方法的干扰抑制性能与其所恢复的干扰数据是否高质量、支持精确的干扰协方差估计有关。结合图像分割提取干扰区域,滤波器设计抑制RFI的处理框图如图3所示。具体的设计算法可参考文献[11]。

图3　结合干扰区域提取的RFI抑制处理框图

假设干扰提取算法所得干扰区域B并得到干扰数据Z,恢复至时域可估计协方差矩阵为R。由于Z中干噪比足够高且海杂波很少,R能够精确表达干扰信息,那么设计的滤波器用于再处理原数据时,脉冲压缩可以高效率地抑制干扰。

4　仿　真

下面采用文献[9]中天波雷达图像进行数据恢复并模拟RFI,验证本文提出的干扰区域精确提取算法和改进的干扰抑制方法。设天波雷达发射连续波,采用波形带宽为20 kHz,采样频率50 kHz,波形周期为10 ms,相干积累周期数512。模拟RFI,合并为雷达接收数据,信号处理采用传统匹配滤波器和快速傅里叶变换做多普勒处理,所得RD图如图1所示,其中多普勒单元约为0.2 Hz,距离单元约为3 km。由图1可见,位于多普勒单元160处的RFI直线很清晰,而位于多普勒单元240处和280处的RFI处于海杂波过渡区域而难以检测,其边缘所在位置难以确定。

采用本文方法进行干扰区域提取和干扰抑制处理。设置动态范围为80 dB,灰度级为255,将RD图转换为灰度图像,如图4所示。可见此时靠近海杂波的干扰直线不明显。采用LOG算子5×5模板运算,处理灰度图像结果如图5所示。可以看到,强海杂波被消除,其幅度和分布规律与噪声区域相近。同时,多普勒单元160的RFI直线边缘清晰可见,多普勒单元240与280处干扰直线的边缘也较清晰。这说明LOG算法能够有效消除海杂波区域和突出干扰线边缘。

图4　含RFI线的RD灰度图

图5　LOG算子处理后图像

采用Canny算子并进行二值化边缘检测,算法参数设置为高斯平滑参数2,高阈值参数0.3,低阈值为高阈值的0.4倍。结果如图6所示。可见,多普勒单元160和280处干扰线边缘清晰,多普勒单元240处的边缘则不明显,甚至出现被截断。这也是本文算法提出要分两次检测来确定边缘线的原因。

图6　Canny算子边缘检测图像

Canny算子边缘检测后,采用分段直线检测算法,设置参数m0=0.1M,α=0.7,β=0.3,检测和提取的射频干扰直线如图7所示。其中，蓝色线段表示初步检测的边缘子线段,红色实线表示再次检测确认的边缘整线段。可以看到,一条明显的RFI直线被检测到,两条与海杂波相接甚至部分覆盖的RFI直线也被准确提取。最后提取的干扰区域B矩阵的1元素位于162～167、237～242、278～283多普勒单元之间。

图7　RFI位置提取结果

下面采用滤波器设计的思路, 进行干扰抑制并观察抑制效果。采用本文提出的干扰提取算法,设计滤波抑制干扰,结果如图8所示。可见,各条干扰线均被抑制干净,海杂波谱基本保持不变。这是因为,干扰区域精确覆盖干扰线,恢复的干扰样本承载所有干扰信息且不被海杂波影响,因而设计的滤波器能够抑制干扰直线的效果良好。

最后仿真传统的边缘直线检测算法,采用传统Canny梯度算子结合Hough变换,检测结果如图9所示。可以看到,不使用LOG算子而直接采用Canny边缘检测算子,邻近海杂波的RFI直线的边缘变得模糊,尤其是靠近海杂波一侧的边缘难以观测。对比图6,说明了采用LOG算子以去除海杂波影响、突出干扰线的必要性。

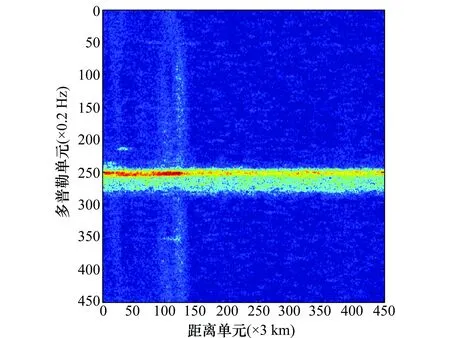
图8　干扰抑制后的RD图

图9　Ganny算子、Hough变换方法的提取结果

仿真中Hough变换只取斜率为零的直线,且令其长度为M,具体做法可参考文献[16]。通过优化Hough变换参数,能够实现的最佳检测结果如图9所示。可以看到,其一大缺陷在于多普勒单元280附近RFI只能检测出单边缘,无法检测靠近海杂波一侧的边缘。如果降低门限以检测该边缘,则会因为门限过低出现虚警。

为考察本文算法对于靠近海杂波的干扰线检测能力,统计检测性能时以干扰线被海杂波覆盖的百分比为指标。例如,图1中多普勒单元280处干扰线的覆盖率为40%。实践经验显示,本文所提算法能够对覆盖率达75%的干扰线实现成功检测,具有很好的实用性。

5　结束语

针对高频雷达的RFI提取问题,本文提出了基于RD图的干扰区域提取算法,实现从当前帧中精确提取RFI数据。区域提取算法采用LOG算子去海杂波、分段和整段边缘线检测等步骤。基于干扰区域恢复的RFI时域数据,可用以辅助提高干扰抑制算法性能。实验结果表明,本文方法能够准确提取被海杂波部分覆盖的RFI区域。本文也以基于滤波器设计的RFI抑制为例,说明了如何结合干扰区域提取算法来改进干扰抑制技术和提高抑制效果的原因。

参考文献：

[1] 周文瑜, 焦培南. 超视距雷达技术[M]. 北京：电子工业出版社, 2008: 132-134.

ZHOU W Y, JIAO P N. Over-the-horizon radar technology[M]. Beijing: Publishing House of Electronics Industry, 2008: 132-134.

[2] GUO X, SUN H, YEO T S. Interference cancellation for high-frequency surface wave radar[J]. IEEE Trans.on Geoscience and Remote Sensing, 2008, 46(7): 1879-1891.

[3] TURCAJ P, ABRAMOVICH Y I, FRAZER G J. Adaptive transient and CW RF interference mitigation in HF OTH radar experimental results[J]. Proceedings of World Academy of Science, Engineering & Technology, 2008, 41(17):242-247.

[4] 文必洋,韩金柱,周企豪,等.高频地波雷达射频干扰抑制新算法的研究[J]. 电波科学学报, 2016,31(4):639-646.

WEN B Y, HAN J Z, ZHOU Q H, et al. New radio frequency interference suppression algorithm in high frequency surface wave radar[J].Chinese Journal of Radio Science,2016,31(4):639-646.

[5] ZHOU H, WEN B. Radio frequency interference suppression in small-aperture high-frequency radars[J]. IEEE Geoscience & Remote Sensing Letters, 2012, 9(4):788-792.

[6] WANG W, WYATT L R. Radio frequency interference cancellation for sea-state remote sensing by high-frequency radar[J]. IET Radar Sonar & Navigation, 2011, 5(4): 405-415.

[7] WANG W, WYATT L. Generalised noise cancellation method for wave estimation by HF surface wave radar[J]. IET Radar Sonar & Navigation, 2014, 8(6):622-631.

[8] 文必洋, 韩金柱, 周企豪,等. 高频地波雷达空域射频干扰抑制算法[J]. 西安电子科技大学学报, 2017, 44(4):132-137.

WEN B Y, HAN J Z, ZHOU Q H, et al. Radio frequency interference suppression algorithm in the spatial domian for high-frequency radars[J]. Journal of Xidian University, 2017, 44(4): 132-137.

[9] LIU Z, SU H, HU Q. Radio frequency interference cancelation for sky wave over-the-horizon radar[J]. IEEE Geoscience & Remote Sensing Letters,2016, 13(3): 304-308.

[10] GURGEL K W, BARBIN Y, SCHLICK T. Radio frequency interference suppression techniques in FMCW modulated HF Radars[C]∥Proc.of the IEEE Oceans Conference, 2007:1-4.

[11] 罗忠涛. 新体制天波超视距雷达信号处理研究[D]. 成都:电子科技大学,2015.

LUO Z T. Study on signal processing for future sky-wave over-the-horizon radar system[D]. Chengdu: University of Electronic Science and Technology of China, 2015.

[12] LUO Z, HE Z, LI J. An effective scheme for radio frequency interference suppression in high-frequency radar[C]∥Proc.of the Radar Conference, 2015: 539-544.

[13] HU J, TONG X, XIE Q, et al. An improved, feature-centric LOG approach for edge detection[C]∥Proc.of the International Conference on Computational Science and Its Applications, 2016:474-483.

[14] 贺强,晏立.基于LOG和Canny算子的边缘检测算法[J].计算机工程, 2011,37(3):210-212.

HE Q, YAN L. Algorithm of edge detection based on LOG and Canny operator[J].Computer Engineering,2011,37(3):210-212.

[15] RONG W, LI Z, ZHANG W, et al. An improved Canny edge detection algorithm[C]∥Proc.of the International Conference on Mechatronics and Automation, 2014:577-582.

[16] LUO Z T, SONG T C, HE Z S, et al. Approach for transient interference detection based on straight line extraction for high-frequency sky-wave radar[J].Electronics Letters,2017,53(9):618-620.