基于两阶段DEA的空中突防兵力方案评价方法

周中良, 程　越, 寇　添, 呙鹏程

(空军工程大学航空航天工程学院, 陕西 西安 710038)

0　引　言

作战方案是作战单元执行任务的基本依据,关系着战斗的胜负,由兵力方案[1]、任务规划[2]、效能评估[3]等要素组成。其中,兵力方案是作战方案的重要组成部分,不同的兵力投入会获得不同的作战效果[4],故对兵力方案择优选取是作战取胜的关键。兵力方案的优选,存在两类原则,一是作战效能的最大化[5],二是效费比的最大化[6],本文以效费比为原则研究兵力方案的优选方法。

本文以飞机编队突防作战的兵力策略优选为背景,运用系统动力学(system dynamics, SD)的方法,构建突防编队依次通过飞机拦截区、地空武器拦截区直至打击目标的突防兵力损失模型,为优选提供较可靠的数据来源。采用数据包络分析(data envelopment analysis, DEA)中序贯型网络模型为评价方法,将突防过程抽象为类型3两阶段DEA的兵力多输入多输出系统,证明其加性与乘性效率分解与类型1不同,并分别从两阶段的输出与输入导向提出新的中立性评价方法,分别用于兵力策略的效率评价与优选。

1　突防兵力损失模型

兵力损失模型是兵力方案优选的基础,是突防飞机编队受拦截影响与拦截方受攻击影响的数学描述,本文将突防过程分为通过飞机拦截区、通过地空武器拦截区两部分,两防空区互不重叠,呈“串联”防御的关系。

如图1所示,突防飞机编队依次通过飞机拦截区、地空武器拦截区,实施对目标群的打击。

图1　突防作战示意图

设定突防方兵力类型有:被掩护机、掩护机、电子对抗兵力、网络化作战兵力。拦截方兵力类型有:拦截机、地空武器、电子对抗兵力、网络化作战兵力。被掩护机仅用于对目标的打击;掩护机用于保护被掩护机,实施对拦截机与地空武器的作战;拦截机用于对被掩护机与掩护机的作战;地空武器分为防空导弹与高炮两种,用于对突防编队的拦截。由于电子对抗可能涉及的作战单元较多,且战术复杂,故在突防模型中以电子对抗能力指数表示;同样地,网络化作战对作战效能的影响也较复杂,以兵力倍增系数表示。电子对抗兵力与网络化作战兵力只考虑投入不考虑损失。采用

系统动力学的方法对突防作战进行建模,该方法利用系统中各要素之间的影响对系统的特性进行研究[7-9]。存量流量图是用于量化模型的基本方法,其中,存量是变量的累积量,流量是变化量,流率是变化的速率[10-12]。本文对两防空区交战中兵力变化影响的因素进行归纳总结,并作出相应的存量流量图。

1.1　飞机拦截区模型

在飞机拦截区中,突防方参与的兵力类型有:被掩护机、掩护机、电子对抗兵力、网络化作战兵力。拦截方参与的兵力类型有:拦截机、电子对抗兵力、网络化作战兵力。对交战过程进行分析,总结出所涉及的存量、流量、辅助变量、常量分别为存量:L1(t)、L2(t)、L3(t);流量:R1(t)、R2(t)、R3(t);辅助变量:Q1(t)、Q2(t)、Q3(t)、q13(t)、q23(t)、q31(t)、C13(t)、C23(t); 常量:q1、q2、q3、P13、P23、P31、A1、M1、A3、M3、T1、k1、k2、k3、k4。

各参数意义如图2所示,其中,数量的单位是“架”,损耗的单位是“架/分钟”,攻击速度的单位是“次/分钟”, 时间单位是“min”。根据存量、流量、辅助变量、常量之间的影响关系,利用vensim 6.0b PLE软件作出存量流量图,因果关系标明极性,且常量用虚线连接。辅助变量具体数学模型参考文献[13]。

q13(t)dt+q1T1

(1)

(2)

(3)

1.2　地面防空区拦截模型

对飞机编队在地空武器拦截区中的交战过程进行分析,总结出所涉及的存量、流量、辅助变量、常量分别为存量:L1(t)、L2(t)、L4(t)、L5(t)、L6(t);流量:R1(t)、R2(t)、R4(t)、R5(t)、R6(t);辅助变量:Q1(t)、Q2(t)、Q4(t)、Q5(t)、Q6(t)、q14(t)、q15(t)、q24(t)、q25(t)、q42(t)、q52(t)、q62(t)、C14(t)、C15(t)、C24(t)、C25(t)、C41(t)、C51(t);常量:q1、q2、q4、q5、P14、P15、P24、P25、P42、P52、P62、A1、M1、A2、M2、A4、A5、T2、k1、k2、k3。

各参数意义如图3所示,与飞机拦截区相同的变量的单位相同,地空导弹与高炮单元及目标的单位是“个”,存量流量图构建方法与飞机拦截区相同。

图3　地空武器拦截区兵力损耗存量流量图

(q14(t)+q15(t))dt+q1T2

(4)

(5)

(6)

(7)

(8)

2　两阶段DEA评价方法

飞机编队在突防中,会依次通过飞机拦截区与地空武器拦截区,最终实现对目标的打击。每一拦截区都会对突防编队造成不同的损失,如掩护机与突防机的损失等,并且收获不同的作战收益,如击毁拦截飞机、避开地空武器等。对这个过程进行效率评价,是兵力方案优选的基础。可见,突防兵力损失模型是一个多输入多输出的系统模型,要评价不同兵力策略的优劣,根本上就是对多输入多输出系统进行效率评价。

DEA是经济、管理等学科中用于多输入多输出系统效率评价的经典方法。决策单元(decision making unit, DMU)是DEA方法中的评价对象,是对DEA所研究对象的统称,本文研究的兵力方案就是DMU的一种。传统的DEA方法将DMU视作“黑箱”,不考虑其内部结构,不能根据DMU内部的投入产出关系评价效率,是传统DEA评价方法的主要缺点。而多阶段DEA适用于对具有网络结构的DMU中每一阶段进行效率评价,为决策提供更加准确的依据[14-16]。文献[17]于1978年提出DEA的第一个模型以来,传统DEA一直将DMU视作仅具有一个阶段的多输入多输出系统,即“黑箱”,忽略DMU内部结构。直到文献[18]于1996年对具有多阶段的DMU研究了效率评价问题。文献[19]对多阶段DEA评价模型与方法进行了总结。文献[20-21]提出了不同种类多阶段网络DEA的评价方法,并对两阶段DEA进行了着重研究。

图4是多阶段DEA系统的示意图,X表示系统外部输入,Z表示系统内部的输入或输出,K表示非末阶段系统外部输出,Y表示末阶段系统外部输出。由突防的过程可知其适用于两阶段DEA评价,两阶段DEA可分为图5所示的4种结构。

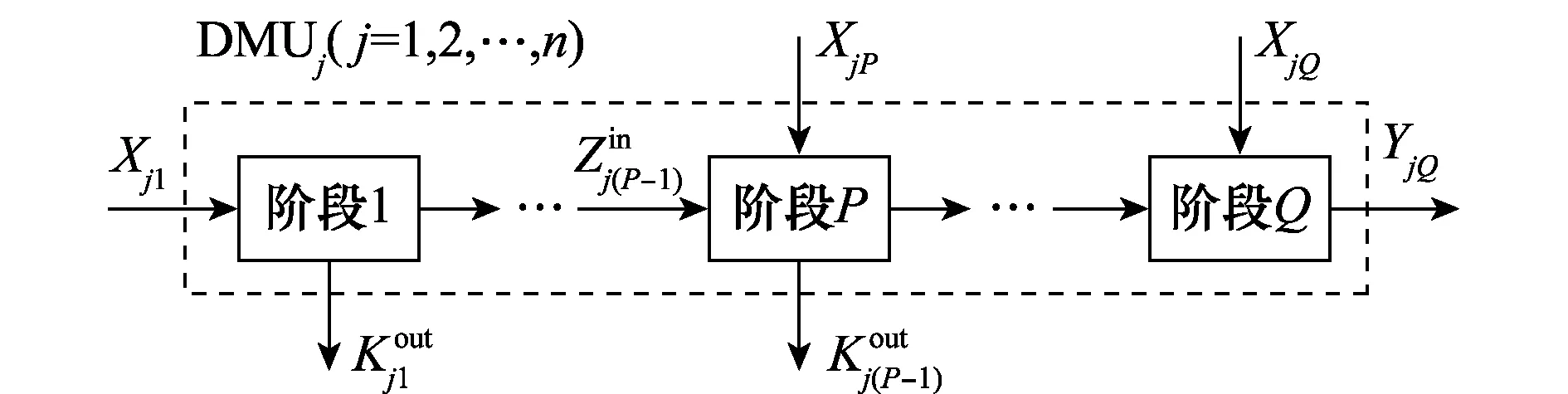
图4　多阶段DEA

图5　两阶段DEA的4种类型

不考虑兵力补充,按照飞机编队依次通过飞机拦截区与地空武器拦截区的流程,根据两个拦截区的兵力损失存量流量图,可以总结出突防作战的兵力输入输出结构如图6所示。

图6　突防作战的兵力输入输出结构

可见,对于突防作战,在阶段1中存在不属于阶段2输入的输出,且阶段2没有外部输入,故适用于两阶段DEA评价中的类型3模型。下面对类型3模型在规模有效情况下[22-24]的效率评价问题进行研究。

2.1　加性效率分解模型

根据加性两阶段DEA模型,假设第j个DMU-DMUj的两阶段整体效率为

(9)

阶段1和阶段2的效率分别为

(10)

则整体效率的加性分解为

(11)

(12)

(13)

(14)

易知,式(14)属于分式规化模型,为简化运算,应用C2变换进行处理,该变换是由Charnes与Cooper两人提出的处理分式规划的方法[25],可以得到

(15)

当式(15)取得最大值时,令(u*,w*,r*,q*)为最优参数组合,则

(16)

(17)

两个阶段效率分解系数的比值为

(18)

2.2　乘性效率分解模型

对类型3的两阶段DEA,由乘性效率分解的定义,可给出其整体效率为

(19)

阶段效率与加性效率分解模型相同,为取得整体效率最大值,根据输入导向,作最优规划,即

(20)

应用C2变换,有

(21)

令(u*,w*,r*,q*)是式(21)的最优参数组合,则

(22)

(23)

2.3　中立性两阶段效率合成

从第2.1节与第2.2节可知,无论是整体效率的加性分解还是乘性分解,其目的都是提出一种两阶段DEA的整体效率评价方法。对于多阶段DEA,除首阶段的输入与尾阶段的输出外,还存在其余输入或输出,这些量在效率评价中的作用是未知的,故整体效率的定义与单阶段DMU不同,存在主观性与多样性。本节对类型3的两阶段DEA中的两个阶段分别从输出导向与输入导向进行效率评价,由两阶段各自效率值的大小,根据不同导向具备的不同最优规划的特性,提出一种中立性合成的两阶段DEA整体效率评价方法,在满足分阶段评价的基础上,为类型3两阶段DEA的整体效率构建客观的评价方法。对阶段1,从输出导向,做出最优规划为

(24)

对阶段2,从输入导向,做出最优规划为

(25)

因式(24)和式(25)限制条件相同,且目标函数可整合,故可合并为一个规划,即

(26)

同样地,应用C2变换,有

min [qXj0wZj0-uYj0(wZj0+rKj0)]

(27)

令(u*,w*,r*,q*)是最优参数组合,则最优解为q*Xj0w*Zj0-u*Yj0(w*Zj0+r*Kj0),且

(28)

以上将根据第一阶段与第二阶段两最优规划进行整合,提出了可根据两阶段合成效率值对整体效率进行评价的方法,避免了因整体效率定义方式的不同所导致的评价结果的主观性与偏见性。可以看出,本文提出的3种类型3两阶段DEA均具有中立性,且无优劣之分。

3　仿真分析

首先设定突防作战中突防方与拦截方的兵力,模型参数以及作战任务要求,根据兵力损耗模型得到所有兵力方案的兵力损耗情况,然后根据构建的3种两阶段DEA效率评价方法对兵力方案进行效率评价,根据任务要求,选择最优兵力方案。

突防方与拦截方兵力及毁伤系数设定如表1和表2所示。作战时间持续20单位,不分波次,任务成功的底线为摧毁50个以上(含50个)目标,拦截方兵力为固定值。

表1　兵力参数

表2　毁伤系数

表2中表示行中兵力对列中兵力的毁伤系数。分配系数均按照平均分配的原则,从突防方的角度对兵力策略进行优选。首先,对可生成所有兵力方案的结果进行推演,兵力方案共有10×12×4×2=960个。由于兵力方案数目较多,不逐一列出。飞机拦截区和地空武器拦截区兵力损失如表3和表4所示。

表3　飞机拦截区兵力损失

表4　地空武器拦截区兵力损失

分别运用类型3两阶段DEA的加性效率分解、乘性效率分解与中立性效率合成方法对960种兵力方案进行效率评价。将所有兵力方案的效率值映射在二维坐标系上,其中横坐标S表示方案,纵坐标E表示效率值,以“红色”“蓝色”“绿色”分别表示表示兵力方案在飞机拦截区效率值、地空武器拦截区效率值、整体效率值。

如图7所示,应用加性效率分解的评价方法,当突防编队通过飞机拦截区时,第392号方案效率值最高,效率值为0.963 5,方案为5架被掩护机、1架掩护机、电子对抗兵力为4、网络化作战兵力为2,但是该方案只能摧毁45.821 5个目标,不符合任务要求。

图7　加性效率分解中飞机拦截区效率值

如图8所示,应用加性效率分解的评价方法,当突防编队通过地空武器拦截区时,第911号方案效率值最高,效率值为0.965 1,方案为10架被掩护机、6架掩护机、电子对抗兵力为4、网络化作战兵力为1,可摧毁84.562 4个目标,可知该方案符合任务要求。

图8　加性效率分解中地空武器拦截区效率值

如图9所示,应用加性效率分解的评价方法,整体上,第673号方案效率值最高,效率值为0.943 3。方案为8架被掩护机、1架掩护机、电子对抗兵力为1、网络化作战兵力为1,可摧毁51.012 2个目标,符合任务要求。

图9　加性效率分解中整体效率值

如图10所示,应用乘性效率分解的评价方法,当突防编队通过飞机拦截区时,第122号方案效率值最高,效率值为0.981 0,方案为2架被掩护机、4架掩护机、电子对抗兵力为1、网络化作战兵力为2,可摧毁11.936 5个目标,不符合任务要求。

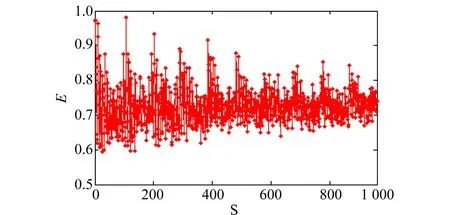
图10　乘性效率分解中飞机拦截区效率值

如图11所示,应用乘性效率分解的评价方法,当突防编队通过地空武器拦截区时,第883号方案效率值最高,为0.974 5,方案为10架被掩护机、3架掩护机、电子对抗兵力为2、网络化作战兵力为1,可摧毁56.968 7个目标,符合任务要求。

图11　乘性效率分解中地空武器拦截区效率 Fig11　Efficiencies in air defense weapons interception zone under multiplicative efficiency decomposition model

如图12所示,应用乘性效率分解的评价方法,整体上,第673号方案效率值最高,效率值为0.9890。与加性效率分解方法所得结果相同。

图12　乘性效率分解中整体效率值

如图13所示,应用中立性两阶段效率合成的评价方法,当通过飞机拦截区时,第392号方案效率值最高,效率值为0.991 1,与加性效率分解方法所得结果相同。

图13　中立性两阶段效率合成中飞机拦截区效率值

如图14所示,应用中立性两阶段效率合成的评价方法,当通过地空武器拦截区时,第883号方案效率值最高,效率值为0.951 3,与乘性效率分解方法所得结果相同。

图14　中立性两阶段效率合成中地空武器拦截区效率值

如图15所示,应用中立性两阶段效率合成的评价方法,整体上,第673号方案效率值最高,效率值为0.972 0,与两种效率分解方法所得评价结果均相同。

图15　中立性两阶段效率合成中整体效率值

综上,应选取第673号作战方案,能够取得最大的整体作战效率值。可以看出,3种方法在评价结果上基本一致,尤其是效率加性分解与乘性分解评价方法所得结果与中立性效率合成评价方法所得结果基本一致,验证了类型3两阶段DEA在效率分解时的中立性。

4　结　论

本文运用系统动力学的方法构建了突防飞机编队依次通过飞机拦截区与地空武器拦截区的兵力损失模型。对类型3两阶段DEA的效率加性分解与乘性分解模型进行推导,并指出其无偏见性,并提出从不同导向综合两阶段效率的中立性评价方法,在仿真实验中证明3种方法的有效性。值得注意的是,当可选兵力种类与数目较多时,可选兵力方案的数目将十分庞大,逐一计算效率值进行优选将耗费较长时间,今后将研究运用近似寻优算法解决该问题的可行性。

参考文献：

[1] 谭鑫,王炜,张茂军.不完备信息条件下基于证据理论的CGF行为决策方法[J].系统工程理论与实践,2013,33(6):1608-1614.

TAN X, WANG W, ZHANG M J. Behavior decision method of CGF with incomplete information based on evidence theory[J]. Systems Engineering-Theory & Practice,2013,33(6):1608-1614.

[2] MOGHADDAM B F, RUIZ R, SADJADI S J. Vehicle routing problem with uncertain demands: an advanced particle swarm algorithm[J].Computers & Industrial Engineering,2012,62(1): 306-317.

[3] XU Y J, WANG Y C, MIU X D. Multi-attribute decision ma-king method for air target threat evaluation based on intuitionistic fuzzy sets[J]. Journal of Systems Engineering and Electronics, 2012, 23(6): 891-897.

[4] 牛德智,陈长兴,班斐,等.基于效能评估的航空作战进程预测[J].航空学报,2014,35(5): 1416-1423.

NIU D Z, CHEN C X, BAN F, et al. Prediction on air combat process based on effectiveness evaluation[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(5): 1416-1423.

[5] 李响, 邢清华, 董涛. 基于多指标正交实验设计的UAV编队配系优化[J]. 系统工程与电子技术, 2013, 35(2): 331-337.

LI X, XING Q H, DONG T. Deployment optimization of UAV formation based on multi-index orthogonal experimental design[J]. Systems Engineering and Electronics, 2013, 35(2): 331-337.

[6] 张滢, 杨仁农, 左家亮, 等.改进分解进化算法求解动态火力分配多目标优化模型[J]. 兵工学报, 2015, 36(8): 1533-1540.

ZHANG Y, YANG R N, ZUO J L, et al. Improved decomposition-based evolutionary algorithm for multi-objective optimization model of dynamic weapon-target assignment[J]. Acta Armamentarii, 2015, 36(8): 1533-1540.

[7] WHITAKER E L. System dynamics[M]. Surrey: Sweetapple House Cattshell RD Farncombe, 2015: 157-165.

[8] SUN J, ZHENG H, DEMARCO C L, et al. Energy function-based model predictive control with UPFCS for relieving power system dynamic current violation[J]. IEEE Trans.on Smart Grid, 2016, 7(6): 2933-2942.

[9] LUO F J, DONG Z Y, CHEN G, et al. Advanced pattern discovery-based fuzzy classification method for power system dynamic security assessment[J]. IEEE Trans.on Industrial Informatics, 2015, 11(2): 416-426.

[10] PARKS E. A systems-level dynamic model of concussion[J]. Journal of Neurotrauma, 2016, 33(13): 97-106.

[11] GIOSIO D R, HENDERSON A D, WALKER J M, et al. Physics-based hydraulic turbine model for system dynamic studies[J]. IEEE Trans.on Power Systems, 2017, 32(2): 1161-1168.

[12] NAN X, ARANYA C. Parallel identification of power system dynamic models under scheduling constraints[J]. IEEE Trans.on Power Systems, 2016, 31(6): 4584-4594.

[13] 穆中林,周中良,于雷,等.编队对地攻击作战效能评估的系统动力学方法[J].系统工程理论与实践,2010,30(3):565-570.

MU Z L, ZHOU Z L, YU L. System dynamics method for effectiveness evaluation of formation attacking ground targets[J]. Systems Engineering-Theory & Practice,2010,30(3):565-570.

[14] CAMPOS M S, FERNANDEZ-MONTES A, GAVILAN J M, et al. Public resource usage in health systems: a data envelopment analysis of the efficiency of health systems of autonomous communities in Spain[J]. Public Health, 2016, 138(9): 33-40.

[15] WANKE P, BARROS S, MACANDA N P. Predicting efficiency in Angolan banks: a two-stage TOPSIS and neural networks approach[J].South African Journal of Economics,2016,84(3): 461-483.

[16] HOLDEN R, XU B, GREENING P, et al. Towards a common measure of greenhouse gas related logistics activity using data envelopment analysis[J]. Transportation Research Part A-Policy and Practice, 2016, 91(9): 105-119.

[17] CHARNES A, COOPER W W, RHODES E. Measuring the efficiency of decision making units[J].European Journal of Operational Research, 1978, 2(6): 429-444.

[19] CASTELLI L, PESENTI R, UKOVICH W. A classification of DEA models when the internal structure of the decision making units is considered[J]. Annals of Operations Research, 2010, 173(1): 207-235.

[20] DIMITRIS D K, KORONAKOS G, SOTIROS D. Composition versus decomposition in two-stage network DEA: a reverse approach[J].Journal of Productivity Analysis,2016,45(1):71-87.

[21] DIMITRIS D K, SOTIROS D, KORONAKOS G. A network DEA approach for series multi-stage processes[J]. Omega, 2016, 61: 35-48.

[22] DAS M, PATRA S. Productivity and efficiency of public sector banks in India after the global financial crisis[J]. IUP Journal of Bank Management, 2016, 15(2): 50-62.

[23] UEASIN N, LIAO S Y, WONGCHAI A. The technical efficiency of rice husk power generation in Thailand: comparing data envelopment analysis and stochastic frontier analysis[J]. Energy Procedia, 2015, 75(10): 2757-2763.

[24] UEASIN N, WONGCHAI A, NONTHAPOT S. Performance assessment and optimization of biomass steam turbine power plants by data envelopment analysis[J]. International Journal of Energy Economics and Policy, 2015, 5(3): 668-672.

[25] CHARNES A, COOPER W W. Programming with linear fractional functionals[J].Naval Research Logistics,2010,9(3/4): 181-186.