近场单发多收合成孔径雷达成像的频域算法
朱荣强, 周剑雄, 付 强
(国防科技大学电子科学学院ATR实验室, 湖南 长沙 410073)
0 引 言
合成孔径雷达(synthetic aperture radar,SAR)由于其独特的优势,已被广泛用于遥感、监测等领域。但是,传统的SAR只能获得目标的二维散射系数分布,因此丢失了目标的部分信息,并且成像结果存在一些缺点。近年来,将多站阵列与孔径合成技术相结合的新成像体制成为了研究热点[1-7]。该成像结构利用与孔径合成方向相正交的阵列天线获得三维成像能力,但是与SAR成像相比,由于多站阵列中收发阵元分置,使得其成像处理变得更为复杂。
在SAR成像中,距离迁徙算法(range migration algorithm,RMA)是一种常用的精确成像算法。该方法通过将回波数据变换至波数域进行补偿,有效提高了成像效率并且保证了成像精度[8-9]。但是,RMA不能直接用于多站阵列成像。为了将RMA拓展用于多站阵列成像,文献[10]根据等效相位中心原理将多发多收(multiple-input multiple-output,MIMO)阵列回波数据转换为单站格式,并利用参考信号对转换后的数据进行补偿;文献[11-12]利用多平面波近似,将RMA拓展至单发多收(single-input multiple-output,SIMO)阵列成像,并将波数空间进行分割以降低近似误差;文献[13]利用二阶泰勒展开,推导了SIMO-SAR的近似波数谱。这些方法利用近似简化成像处理的同时降低了成像精度。文献[14]将RMA拓展用于近场MIMO阵列,但是要求收发阵元的采样间隔必须满足奈奎斯特采样定理,无法适用于一般的MIMO阵列。文献[15]提出了一种适用于SIMO阵列的频域成像算法,该方法利用基于快速傅里叶变换(fast Fourier transform, FFT)的子成像结构有效提高了成像效率并且避免了插值,但是该方法不能直接用于SIMO-SAR成像。
在多站阵列成像处理中,后向投影算法(backprojection algorithm,BPA)是最为常用的算法之一。该方法逐点相干累加成像,因此具有很高的成像精度,并且可以适用于多种成像体制。但是,用于三维成像时,BPA的成像效率较低。
本文提出了一种适用于SIMO-SAR的频域成像算法。该方法首先将回波数据变换至波数域,然后对波数域数据进行扩维以实现补偿和插值,最后利用降维累加得到了散射系数分布的三维傅里叶变换。该方法在波数域精确补偿了波前弯曲,因此可以用于近场三维高精度成像,并且该方法采用频域成像结构显著提高了成像效率。
1 成像算法
SIMO-SAR的成像几何模型如图1所示。

图1 SIMO-SAR成像几何模型
以目标中心为原点建立直角坐标系O-XYZ,X轴、Y轴和Z轴分别表示方位向、距离向和高度向。SIMO阵列由一个发射阵元和NR个均匀分布的接收阵元组成,阵列平行于X轴并沿高度向进行扫描。将接收阵元的位置记为(u,y0,h),发射阵元的位置记为(xt,y0,h),目标上任意一点的位置记为(x,y,z),对应散射系数为σ(x,y,z)。假设发射信号为步进频信号,则回波信号可以表示为
s(u,k,h)=∭σ(x,y,z)e-jkRte-jkRrdxdydz
(1)
式中,k=2πf/c表示波数,f表示频率,c表示光速;Rt和Rr分别表示发射阵元和接收阵元与任意目标间的距离,具体关系式为
(2)
(3)
由时域相关法的成像原理可得散射系数分布的估计为

∭s(u,k,h)ejkRtejkRrdudkdh
(4)
式中,指数项表示球面波传播,利用球面波分解原理可以将其分解为
(5)
(6)
式中,kv和ku的具体关系式为
(7)
(8)
将式(5)和式(6)代入式(4)可得
(9)
式中,S′(ku,k,h)表示回波信号沿u方向的傅里叶变换。式(9)中的第3项利用球面波分解可得
(10)
其中
(11)
利用式(10),式(9)可以简化为
ej(ku+kv)xejkyyejkzzdkudkvdkdkz
(12)
式中,S(ku,k,kz)表示信号S′(ku,k,h)沿h方向的傅里叶变换。为了能够补偿指数项e-jkyy0,以及便于实现插值,将信号S(ku,k,kz)沿kv向进行扩维,扩维前后信号的关系为
(13)
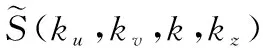
ej(ku+kv)xejkyyejkzzdkudkvdkdkz
(14)

ejkyyejkzzdkudkvdkydkz
(15)

(16)
降维累加运算将分布在ku-kv域内的数据累加至kx域,降维累加后的信号与散射系数分布之间的关系为
∭F(kx,ky,kz)ejkxxejkyyejkzzdkxdkydkz
(17)
从式(17)可以看出,对降维累加后的数据利用三维逆傅里叶变换就可以得到散射系数分布。
2 算法实现及运算量分析
算法的流程图如图2所示。
具体成像步骤如下:
步骤1利用二维FFT得到回波信号沿u和h方向的傅里叶变换S(ku,k,kz)。为了避免波数谱产生混叠,回波数据在方位向和高度向的采样间隔Δu和Δh必须满足
(18)
(19)
式中,λmin表示最大工作频率对应的波长;θx和θz分别表示天线在方位向和高度向的波束角。为了便于分析运算量,近似认为所有FFT均是基二FFT。该步骤的运算量近似为
C1≈5NuNkNzlog2(NuNz)FLOP
(20)
式中,Nu和Nz分别表示回波数据沿方位向和高度向傅里叶变换的点数;Nk表示回波数据的频率采样点数,运算量的单位为浮点运算(floating-point operation,FLOP)。
步骤2将波数域数据沿kv向进行扩维,并补偿指数项e-jkyy0。扩维后的信号在kv向的分布区间由式(7)决定。分布间隔应与波数域数据在ku向的分布间隔相等,以便于实现降维累加。该步骤的运算量为
C2=6NuNkvNkNzFLOP
(21)
式中,Nkv表示扩维后的信号在kv向的长度。
步骤3对扩维后的信号沿ky向进行插值,得到在ky域内均匀分布的数据。采用线性插值,该步骤的运算量近似为
C3≈6NuNkvNyNzFLOP
(22)
式中,Ny表示插值后的数据在ky向的长度。
步骤4将分布在ku-kv-ky-kz域的数据降维累加至kx-ky-kz域。该步骤的运算量近似为
C4≈2(NuNkv-Nx)NyNzFLOP
(23)
式中,Nx表示降维累加后的信号在kx域中的分布长度。
步骤5利用三维IFFT得到成像结果。该步骤的运算量近似为
C5≈5NxNyNzlog2(NxNyNz) FLOP
(24)
由分析可得该算法的运算量约为
Cp≈5NuNkNz[log2(NuNz)+1.2Nkv]+8NuNkvNyNz+
5NxNyNz[log2(NxNyNz)-0.4]FLOP
(25)
在相同成像条件下,BPA的运算量为
CBPA≈8NRNhNxNyNzFLOP
(26)
式中,Nh表示回波数据在高度向的采样点数。
比较式(25)和式(26)可以看出,本文的方法与BPA相比显著降低了运算量。
3 实验验证
3.1 仿真数据验证
采用仿真实验比较近似RMA[11-12]、BPA和本文方法的成像效果。仿真目标由9个理想点目标组成,位置如图3所示。SIMO阵列由1个发射阵元和101个接收阵元组成,接收阵元间隔6 mm,发射阵元位于接收阵列的中心。SIMO阵列沿高度向的扫描间隔为3.5 mm,采样点数为161。仿真发射信号为步进频信号,工作频率为30~40 GHz,频率步进间隔为100 MHz。目标距离阵列300 mm。3种算法的仿真成像结果如图4所示。从图4(a)和图4(b)可以看出,采用近似RMA成像时,非原点处目标的成像结果出现了散焦和位置偏移,这是因为,近似RMA在成像处理中采用了平面波近似,只能对原点处的目标实现精确重构。从图4(c)~图4(f)可以看出,采用BPA和本文方法能很好地实现对目标的重构,并且本文方法成像结果的旁瓣水平略低于BPA成像结果的旁瓣水平。
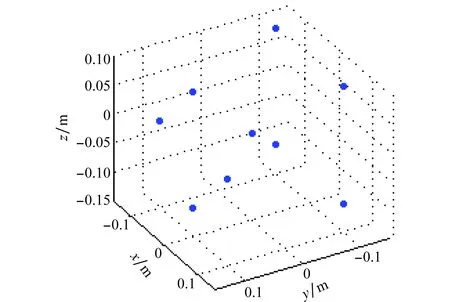
图3 仿真目标设置
采用成像结果的几何均方根误差和熵衡量算法的成像质量。几何均方根误差可以反映成像结果的位置重构精度,几何均方根误差大于一个成像网格点间隔时,表明图像存在位置重构误差;熵可以反映图像的聚焦效果,熵越小则图像的聚焦越好。两个指标的计算公式分别为
(27)
(28)

(29)
由式(27)和式(28)计算得到的几何均方根误差和熵如表1所示。

图4 仿真成像结果

参数近似RMABPA本文方法几何均方根误差/mm6.920.460.46熵11.2911.1810.67
从表1可以看出,近似RMA的几何均方根误差大于一个像素间隔,表明近似RMA对目标的位置重构存在误差,这会导致成像结果出现变形,影响后续图像解译。BPA和本文方法的几何均方根误差相同,均小于一个像素间隔,表明本文方法能精确地重构出目标的几何分布。并且本文方法成像结果的熵要小于BPA成像结果的熵。
3.2 实测数据验证
采用实测数据验证本文方法对实际目标的成像有效性。目标由一把剪刀和一个金属小球组成,如图5所示。目标距离阵列约150 mm,其余参数与仿真实验中的参数设置相同。采用本文方法和BPA的成像结果如图6所示。为了便于比较两种算法的性能,两种算法的成像网格点均为256(方位向)×64(距离向)×256(高度向),并且成像处理中不采用加窗处理。

图5 目标图像


图6 成像结果
比较两个算法的成像结果可以看出,两个算法均实现了对目标的精确重构,并且成像效果相同。表2给出了由式(25)和式(26)计算得到的两个算法的近似理论运算量和实际成像时间。两种算法均通过Matlab实现,并且在相同环境下运行。从表2可以看出,本文方法的运算量要显著小于BPA。

表2 理论运算量与成像时间
注1):GFLOP=109FLOP。
4 结 论
本文针对SIMO-SAR提出了一种频域成像算法。该方法通过将波数域数据进行扩维,在波数域实现了对波前弯曲的精确补偿,因此成像精度较高,并且可用于近场三维成像。另外,从理论上分析了该方法的运算量要远小于BPA。实验结果也表明了该方法可以获得与BPA相同的成像效果,但是显著降低了运算量。本文的研究对于近场多站阵列成像具有一定的借鉴意义。
参考文献:
[1] ZHUGE X,YAROVOY A G. A sparse aperture MIMO-SAR-based UWB imaging system for concealed weapon detection[J]. IEEE Trans.on Geoscience Remote Sensing,2011,49(1):509-518.
[2] GUMBMANN F, SCHMIDT L P. Millimeter-wave imaging with optimized sparse periodic array for short-range applications[J]. IEEE Trans.on Geoscience Remote Sensing, 2011, 49(10): 3629-3638.
[3] WEI M, GILLES M. Initial ARTINO radar experiments[C]∥Proc.of the 8th European Conference on Synthetic Aperture Radar, 2010: 1-4.
[4] KRIEGER G. MIMO-SAR: opportunities and pitfalls[J]. IEEE Trans.on Geoscience Remote Sensing, 2014, 52(5): 2628-2645.
[5] 温鑫, 黄培康, 年丰,等. 主动式毫米波近距离圆柱扫描三维成像系统[J]. 系统工程与电子技术, 2014, 36(6): 1044-1049.
WEN X,HUANG P K, NIAN F, et al. Active millimeter-wave near-field cylindrical scanning three-dimensional imaging system[J].Systems Engineering and Electronics,2014,36(6):1044-1049.
[6] 周伟,刘永祥,黎湘,等.MIMO-SAR技术发展概况及应用浅析[J].雷达学报,2014,3(1): 10-18.
ZHOU W, LIU Y X, LI X, et al. Brief analysis on the development and application of multi-input multi-output synthetic aperture radar[J]. Journal of Radars, 2014, 3(1): 10-18.
[7] 董会旭, 张永顺,冯存前,等.基于线阵的MIMO-ISAR二维成像方法[J]. 电子与信息学报, 2015, 37(2): 309-314.
DONG H X, ZHANG Y S, FENG C Q, et al. Two-dimensional imaging using MIMO radar and ISAR technique based on linear array[J]. Journal of Electronics and Information Technology, 2015, 37(2): 309-314.
[8] SOUMEKH M. Synthetic aperture radar signal processing with Matlab algorithms[M]. New York: Wiley, 1999.
[9] 谭维贤,洪文,王彦平,等.基于波数域积分的人体表面微波三维成像算法研究[J].电子与信息学报,2009,31(11):2541-2545.
TAN W X, HONG W, WANG Y P, et al. Three-dimensional microwave imaging algorithm for the surface of the human body based on wavenumber domain integration[J]. Journal of Electronics and Information Technology,2009,31(11):2541-2545.
[10] WILLIAM F M, JAMES D K, JANUSZ J M, et al. Development of a high-throughput microwave imaging system for concealed weapons detection[C]∥Proc.of the IEEE International Symposium on Phased Array System and Technology, 2016: 1-6.
[13] DU L, WANG Y P, HONG W, et al. A three-dimensional range migration algorithm for downward-looking 3D-SAR with single-transmitting and multiple-receiving linear array antennas[J]. EURASIP Journal on Advances in Signal Processing,2010,2010(1): 1-15.
[14] ZHUGE X, YAROVOY A G. Three-dimensional near-field MIMO array imaging using range migration techniques[J]. IEEE Trans.on Image Processing, 2012, 21(6): 3026-3033.
[15] ZHU R Q, ZHOU J X, TANG L, et al. Frequency domain imaging algorithm for single-input-multiple-output array[J]. IEEE Geoscience Remote Sensing Letters, 2016, 13(14): 1747-1751.

