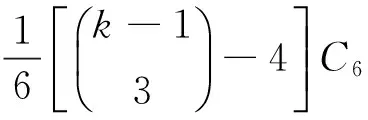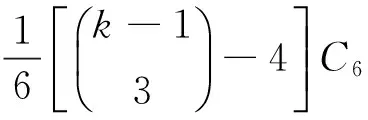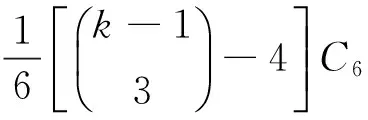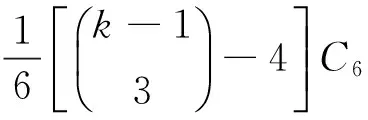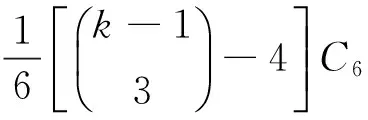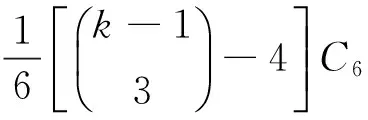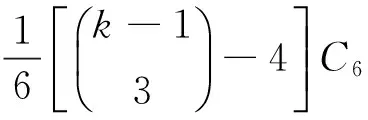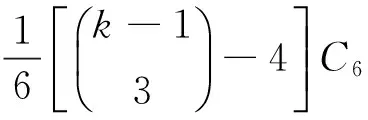mC6的点可区别全染色*
何玉萍,王治文,陈祥恩
(1. 西北师范大学数学与统计学院,甘肃 兰州 730070;2. 宁夏大学数学与统计学院,宁夏 银川 750021)
随着图的染色问题在现实生活中的广泛应用,它逐渐地成为被许多学者研究的重要领域之一。起源于网络问题,生物,信息科学,计算机科学,点可区别正常边染色和点可区别正常全染色问题是有趣和困难的问题。文献[1-3]探讨了图的点可区别正常边染色。本文研究一类图的点可区别正常全染色。
设f:V∪E→{1,2,…,k}为G=(V,E)的一个正常全染色。任意的v∈V, 将与v关联的边的色以及v的颜色组成的集合,称作v的色集合或调色板,记为Cf(v)或C(v),即C(v)={f(vw)|vw∈E}∪{f(v)}。
若任意的u,v∈V,有C(u)≠C(v),dG(u,v)=diam(G),则称f为G的点可区别全染色(简称为VDTC)。 若G的点可区别全染色使用了k种颜色, 则称f为G的k-点可区别全染色(简称为k-VDTC)。
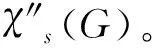
对于图G,用ni(G)表示图G的度为i的顶点个数, 且记
显然有χvt(G) ≥μ(G)。
张忠辅等[4]首次提出图的点可区别(正常)全染色,并且确定了完全图, 完全二部图, 轮, 扇, 双星, 路, 圈, 两条同阶路的联图,n阶路与n圈的联图, 两条同阶圈的联图等图类的点可区别全染色数, 并提出了下面的猜想。
VDTC猜想χvt(G) =μ(G) 或μ(G)+1。
文献[5-8]给出了mK4,mC3,mC4和mC5的点可区别全染色数的相关结果,本文讨论了m个长为6的圈的不交并mC6的点可区别全染色,并且确定了mC6的点可区别全色数。文中结论表明 VDTC 猜想对于图mC6是成立的。文[9-10]对图的奇优美性及完美匹配计数给出了相关结论。
1 准备工作
首先, 对任意的n≥ 9,构造 (n-2)×(n-2)方阵An,并且使矩阵An的元素是空集或集合{1,2,…,n}的含n的3-子集:
设1≤i1 显然, 矩阵An的6×1子矩阵B必是一个好组, 反之未必。如图1所示,C6的6个顶点的色集合分别是 {c1,c2,c3}, {c3,c4,c5}, {c5,c6,c7}, {c7,c8,c9}, {c9,c10,c11} 和 {c11,c12,c1}。记这种染色为f(c1,c2,c3,c4,c5,c6,c7,c8,c9,c10,c11,c12)。 图1 C6 的VDTC f (c1, c2, c3, c4, c5, c6, c7, c8, c9, c10, c11, c12)Fig.1 VDTCf(c1, c2, c3, c4, c5, c6, c7, c8, c9, c10, c11, c12) of C6 引理1当i≡1(mod 6),j=1,2, …,n-2, 并且An[i,i+1,i+2,i+3,i+4,i+5 |j]中的元素都不是空集时, 则An[i,i+1,i+2,i+3,i+4,i+5 |j]是一个好的6×1的子矩阵。 证明当i≥1时,显然,An[i,i+1,i+2,i+3,i+4,i+5 |j]的唯一一列的六个非空子集{n,j,j+i}, {n,j,j+i+1},…, {n,j,j+i+5}恰是在点可区别全染色f(n,j+i,j,j+i+1,n,j+i+2,j,j+i+3,n,j+i+4,j,j+i+5)下,C6 的全体顶点的色集合。 如果矩阵An的元素既不是引理1中任意好的6×1子矩阵的元素也不是空集, 那么称矩阵An的元素是矩阵An的剩余元素。 由于引理2-引理5的证明过程类似, 下面仅给出引理5的详细证明。 证明由引理1, 只需考虑矩阵An的剩余元素。 情形1当n≡6(mod 12)。对i≡1 (mod 12), 6≤i≤n-12。考虑矩阵An在第i,i+1,i+2,i+3,i+4,i+6,i+7,i+8,i+9和i+10列的剩余元素恰能划分成5个好组,相应的C6的VDTC分别是f(n,n-5,i,n-4,n,n-3,i,n-2,n,i,n-1,i+4),f(n,n-4,i+1,n-3,n,n-2,i+1,n-1,n,n-2,i+3,n-1),f(n,n-5,i+6,n-4,n,n-3,i+6,n-2,n,i+6,n-1,i+10),f(n,n-4,i+7,n-3,n,n-2,i+7,n-1,n,n-2,i+9,n-1)和f(n,n-3,i+2,n-2,n,i+2,n-1,i+8,n,n-3,i+8,n-2)。 矩阵An在第1,2,3和4列的剩余元素恰能划分成1个好组, 相应的C6的VDTC是f(n,n-4,1,n,n-3,2,n,n-2,3,n,n-1,4)。 显然,An的剩余元素 {n,1,n-2},{n,1,n-1}, {n,2,n-2} 和 {n,2,n-1}不属于任何一个好组。 情形2n≡ 9(mod 12)。对i≡1(mod 12), 9≤i≤n-12。考虑矩阵An在第i,i+1,i+2,i+3,i+4,i+6,i+7,i+8,i+9和i+10列的剩余元素恰能划分成5个好组, 相应的C6的VDTC分别是f(n,n-5,i,n-4,n,n-3,i,n-2,n,i,n-1,i+4),f(n,n-4,i+1,n-3,n,n-2,i+1,n-1,n,n-2,i+3,n-1),f(n,n-5,i+6,n-4,n,n-3,i+6,n-2,n,i+6,n-1,i+10),f(n,n-4,i+7,n-3,n,n-2,i+7,n-1,n,n-2,i+9,n-1)和f(n,n-3,i+2,n-2,n,i+2,n-1,i+8,n,n-3,i+8,n-2)。 矩阵An在第3,4,5,6和7列的剩余元素恰能划分成2个好组, 相应的C6 的 VDTC分别是f(n,n-5,3,n-4,n,3,n-3,4,n,n-4,4,n-2) 和f(n,n-3,5,n-2,n,5,n-1,7,n,n-1,6,n-2)。 显然,An的剩余元素{n,1,n-1},{n,3,n-2},{n,3,n-1}和{n,4,n-1}不属于任何一个好组。 证明显然有χvt(mC6)≥μ(mC6)=k。因此只需给出mC6的k-VDTC 染色即可。 当2≤m≤3,χvt(mC6)≥6,下面给出mC6的6-VDTC染色。3个C6能被f(1,2,3,4,2,1,4,1, 3,4,6,5),f(5,2,1,3,5,1,4,3,5,4,2,3)和f(6,2,1,3,6,1,4,2,6,5,2,3)分别染色, 所以χvt(3C6)=6。此时遗留下的3-子集为{6,3,5}和{6,4,5}, 而由3C6的染色很容易得到 2C6的 6-VDTC。 当4≤m≤5,χvt(mC6)≥7, 在3C6的基础上只需给出第4,5个C6的染色,分别如下:f(7,2,1, 3,7,4,1,5,7,1,6,5)和f(7,3,2,4,7,5,2,6,7,4,3,5)。所以χvt(5C6)=7。此时遗留下的3-子集为{6,3,5}, {6,4,5},{7,3,6},{7,4,5}和{7,4,6}, 而由5C6的染色很容易得到4C6的 7-VDTC。 当6≤m≤9,χvt(mC6)≥8,在5C6的基础上只需给出第6,7,8,9个C6的染色即可。mC6(m=6,7,8)的8-VDTC染色分别是f(8,2,1,3,8,4,1,5,8,6,1,7),f(8,3,2,4,8,5,2,6,8,2,7,6)和f(8,4,3,5,8,6,3,7,8,6,5,7)。由于{{6,3,5},{6,4,5},{7,3,6},{7,4,6},{8,4,6},{8,4, 7}}是一个好组, 因此可给第9个C6用f(6,3,5,4,6,3,7,6,4,7,8,4)进行染色。 此时遗留下的3-子集为{7,4,5}和{8,4,5},而由9C6的染色很容易得到mC6(m=6,7,8)的 8-VDTC。 当 10≤m≤14,χvt(mC6)≥9。在9C6的基础上只需给出第10,11,12,13,14个C6的染色即可。mC6(m=10,11,12,13)的9-VDTC染色分别是f(9,2,1,3,9,4,1,5,9,6,1,7),f(9,3,2,4,9,5,2, 6, 9, 7, 2,8),f(9,4,3,5,9,6,3,7,9,3,8,1) 和f(9,5,4,6,9,7,4,8,9,7,8,6)。由于{{7,4,5}, {8,4,5}, {9,5,6}, {9,5,7}, {9,5,8},{9,6,7}}是一个好组, 因此可给第14个C6用f(7,5,4,8,5,6,9,7,5,8,9,6)进行染色。至此,已把{1,2,…,9}中的所有 3-子集都用完。由14C6的9-VDTC易得到mC6(10≤m≤13)的9-VDTC。 注意:如果{1, 2,…,k} 的一个3-子集是mC6在k-VDTCg下的一个顶点的色集合, 那么这个3-子集称为在g下用完。 定理1说明VDTC 猜想对mC6是成立的。 参考文献: [1]BURRIS A C, SCHELP R H.Vertex-distinguishing proper edge-colorings [J]. J of Graph Theory, 1997, 26(2): 73-82. [2]BALISTER P N, RIORDAN O M, SCHELP R H. Vertex-distinguishing edge colorings of graphs [J]. J Graph Theory, 2003, 42: 95-109. [3]BAZGAN C, HARKAT-BENHAMDINE A, LI H, et al. On the vertex-distinguishing proper edge-colorings of graphs [J]. J of Comb Theory(Series B), 1999, 75: 288-301. [4]ZHANG Z F, QIU P X, XU B G, et al. Vertex-distinguishing total colorings of graphs [J]. Ars Combinatoria, 2008, 87: 33-45. [5]陈祥恩,王治文,马彦荣,等.mK4的点可区别全染色[J]. 吉林大学学报(理学版), 2012, 50(4): 686-692. CHEN X E, WANG Z, MA Y R, et al. Vertex-distinguishing total colorings ofmK4[J]. Journal of Jilin University (Science Edition), 2012, 50(4): 686-692. [6]辛小青,王治文,陈祥恩,等. 点不交的m个C3的并的点可区别全染色[J]. 吉林大学学报(理学版), 2012, 50(2): 251-257. XIN X Q, WANG Z W, CHEN X E, et al. Vertex distinguishing total chromatic number ofmC3[J]. Journal of Jilin University (Science Edition), 2012, 50(2): 251-257. [7]辛小青,陈祥恩.m个点不交的C4的并的点可区别全染色[J]. 山东大学学报(理学版), 2010, 45(10): 35-39. XIN X Q, CHEN X E. Vertex distinguishing total chromatic number ofmC4[J]. Journal of Shandong University (Natural Science), 2010, 45(10): 35-39. [8]CHEN X E, MA Y R, YANG F, et al. Vertex-distinguishing total colorings ofmC5[J], Applied Mechanics and Materials, 2013, 321/324: 578-581. [9]孙慧,姚兵. 探索圈龙图的奇优美性[J]. 中山大学学报(自然科学版), 2017, 56(4): 9-15. SUN H, YAO B. Exploring the odd gracefulness of cyclic-dragon graphs [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2017, 56(4): 9-15. [10]唐保祥,任韩. 2类图完美匹配数目的解析式[J].中山大学学报(自然科学版), 2016, 55(4): 15-17. TANG B X, REN H. The analytic formula of the number of perfect matchings of two types of graphs [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 55(4): 15-17.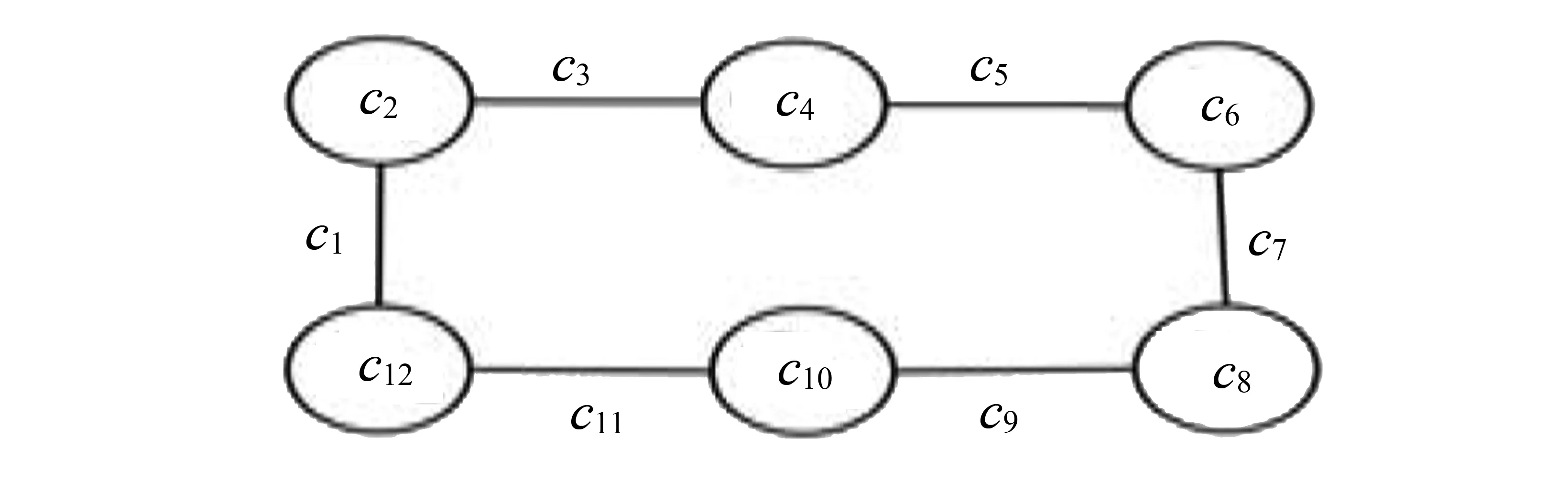
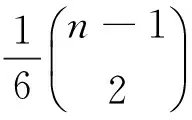

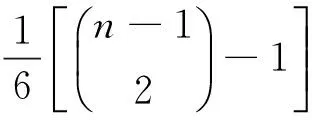

2 主要结果