挖掘课本习题功能，拓宽数学思维空间——一道课本习题的延伸与拓展

☉湖北武汉市第四十五中学 叶志刚

数学课程标准指出：“数学教学活动必须建立在学生的认知发展水平上和已有的知识经验基础之上”“教师应激发学生的学习积极性，向学生提供充分从事数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解与掌握基本的数学基础知识与技能、数学思想方法，获得广泛的数学活动的经验”.课本例题、习题作为渗透新理念、传授知识、培养能力的主要载体，教师应进行充分挖掘和研究，为学生创设合理的学习情境，构建开放的学习环境.

在现实的数学教学中，教师迫于考试压力而拼命补充课外习题，让学生大量地、单调地重复着某个或某几个方法和技能，而对于课本上的例题、习题的讲解基本上是蜻蜓点水，一带而过，忽视了课本例题、习题的潜在功能.课本上的例题、习题蕴含着许多中学阶段用到的数学思想方法.

用心领会课本的精髓，挖掘出例、习题设计的内在教育价值，精选课本中的典型例、习题，进行充分运用、挖掘、延伸、改造，能有效提高教学效率，帮助学生实现知识的整合、方法的迁移，提升学生综合运用知识的能力.

下面对新人教版教材一道经典习题作如下拓展延伸：

课本原题：（人教版八年级数学上册P83第12题）如图1，△ABD、△AEC都是等边三角形，求证：BE=DC.

由已知条件易证AB=AD，∠BAE=∠DAC，AE=AC，则△ABE≌△ADC，因此BE=DC.

此题看似简单，如果深入挖掘则能得到一些新的结论，从而拓展学生的思维空间，提升学习能力.

一、设计递进问题，将数学思维引向深入

如图2，设BE、DC交于点F，连接AF，设置递进问题：

问题（1）：你能求∠BFD的度数吗？

如图3，由上面的证明过程可知△ABE≌△ADC，因此∠ABE=∠ADC.又∠1=∠2，则∠BFD=∠BAD=60°.

问题（2）：FA是∠DFE的角平分线吗？

如图4，过点A作AG⊥DC于G，AH⊥BE于H.因为△ABE≌△ADC，所以S△ABE=S△ADC，BE=DC，由此易知AG=AH，故FA是∠DFE的角平分线.

如图4，由问题（1）知∠BFD=60°，所以∠DFE=120°.

由问题（3）知FA是∠DFE的角平分线，所以∠AFH=60°，可求得AH=3.由勾股定理可得EH=4，BH=9，所以BE=13，故S=BE·AH=△ABE

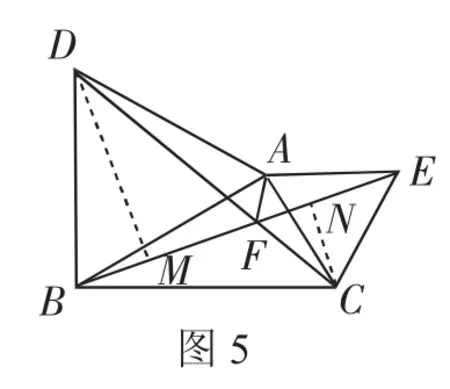
问题（4）：在问题（3）的条件下，求点D、C到直线BE的距离和.

如图5，分别过点D、C作DM⊥BE于M，CN⊥BE于N.因为∠BFD=60°，所以DM=FD·sin∠DFM=FD.同理，CN=FC.所以DM+CN=（FD+FC）=DC=BE=，即点D、C到直线BE的距离和为

问题（5）：求证：FA+FB+FC=CD.

如图6，在DC上截取DG=BF，连接AG.易证△GAD≌△FAB，可得AG=AF，即可判定△FAG为等边三角形，可得AF=GF，即可证FA+FB+FC=CD.

问题（6）：将△AEC绕点A旋转一周，则点F运动的轨迹是什么？

如图7，由问题（1）可知∠BFD=60°，将△AEC绕点A旋转一周，△ABE≌△ADC总成立，故∠BFD=60°总成立.由圆周角定理可推知点F的运动轨迹是一段圆弧.

……

类似的问题还可以设置很多，解决这些问题的核心知识，就是由课本原题所推理出的基本结论，即当条件为△ABD、△AEC都是等边三角形时，有结论：①△ABE≌△ADC；②∠BFD=60°；③FA平分∠DFE.通过这些基本结论的分析运用，让学生在问题的解答中暴露思维过程，加深对数学问题的理解，培养学生数学思维的深刻性.以课本原题为基础设计的层层递进的问题，让学生在分析问题、解决问题的过程中，学会研究问题的实质，发现问题之间的联系，从而提高思维能力.这些一个比一个深入的问题情境，能激发学生积极思考、深入探研、系统掌握知识，让学生对知识的理解不仅仅停留在表面，而是能够较好地建立知识体系，并用知识体系灵活解决实际问题.

二、将问题特殊化，探寻数学思维新的生长点

将课本原题中的△AEC绕点A旋转，使得点C在BA的延长线上时（将问题特殊化往往是数学思维的一个生长点），如图8，设直线BE、DC分别交直线AD、AE于点K、L，除了△ABE≌△ADC，还有其他三角形全等吗？

因为△ABE≌△ADC，所以∠ABK=∠ADL.

又∠BAK=∠DAL=60°，BA=DA，所以△ABK≌△ADL.

同理可证△AEK≌△ACL.

如图9，连接KL，KL与BC平行吗？

由△ABK≌△ADL，可得AK=AL.又因为∠KAL=60°，所以△AKL是等边三角形，故∠ALK=∠EAC=60°，所以KL∥BC.

当点C在线段BA上时，如图10，KL与BC还平行吗？

此时图形虽然发生了变化，但是证明思路还是一样的，同样可证明KL∥BC.

进一步将图形的变换进行到底，如果将图8中△AEC沿BA向右平移c个单位，得到△A′EC，其他条件都不变，如图11，KL与BC还平行吗？

设AB=a，A′C=b，过K、L分别作KM⊥AB，LN⊥AB，垂足分别为M、N.

进一步将问题延伸拓展，如图12，当点A从点B运动到点C时，点F的运动轨迹是什么？如图13，当点C从点A运动到点B时，点F的运动轨迹又是什么呢？

图12中，当点A从点B运动到点C时，∠BFD总等于60°，可知∠AFC=120°，由圆周角定理可推知点F运动的轨迹是圆弧，图13中，当点C从点A运动到点B时，∠BFD=60°，同理可知点F的运动轨迹是圆弧.

通过以上问题的探索、研究，使学生解决问题的方法、思路越来越灵活与深刻，让学生从数学问题的表象，一步一步接触到了数学问题的本质.

对教材中的例、习题进行多层次变换，特别是变换图形的位置、形状，可以训练学生思维的灵活性.通过探究图形在变化过程中所隐含的规律，让学生研究特殊图形与任意图形的区别与联系，通过一静一动，体会特殊与一般的内在关联，动静结合，让学生在静中学法，在动中应用；虽然题目在不断进行变式，但思路还是保持“多变归一”，让学生在经历知识探究的过程中，充分体验“一题多变”的乐趣与“多变归一”的妙趣.

三、改变图形形状，提高类比迁移能力

将课本习题进行推广、拓展和延伸，给学有余力的学生提供思考的空间和发挥的平台.提高学生对数学知识的运用和迁移运用能力，体会数学基本思想方法，培养学生的类比猜想、探究推理能力.

如图14，将课本原题中的条件“△ABD、△AEC都是等边三角形”变为：

（1）“△ABD、△AEC都是等腰三角形，两顶角∠BAD=∠CAE，求证：BE=DC”，可以吗？

（2）“正方形ABGD和正方形ACFE，求证：BE=DC”，可以吗？

（3）再将正方形变为正五边形、正六边形、…、正n边形，能否得到类似结论？

（4）将原题图形中的“形外”变为“形内”，上述结论是否还成立？

……

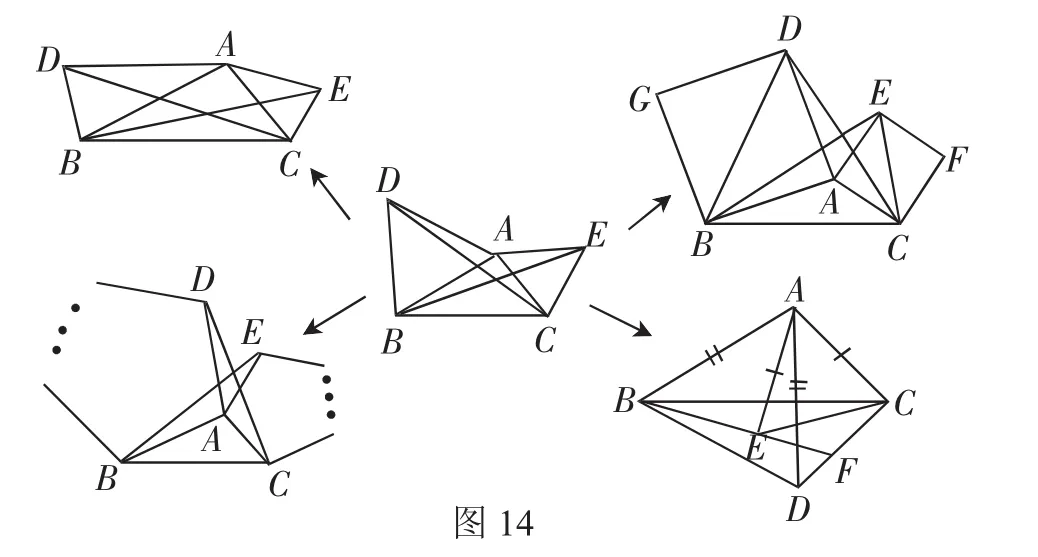
在这些问题中，不论图形发生了怎样的改变，△ABE≌△ADC总成立，故BE=DC.这些问题的设置，使学生在起初的惊奇、疑惑和略加证明后的豁然开朗中发现：异图同解，各尽其妙；不变中有变，变中有不变.达到了“做一题，解一类”的目的，使学生解题、思维的能力得到升华.

以上只是对一道课本习题的一连串思索，然而我们所获得的却远非解答这道习题本身，既让学生掌握了一类问题的规律与内在联系，又使师生获得了研究问题的一些基本方法，同时对减轻学生负担，训练培养学生思维的广阔性、探究性和创造性也有一定的促进作用.

数学教材是一批教育教学专家依据数学课程标准、经过反复审编形成的教学素材，其基本理念、基本要求具有导向性.目前数学教材仍是数学教师教学的基本范本，更是学生数学学习中获得数学知识、数学思想方法，积累基本活动经验，形成数学素养的重要载体.因此平时教学时，教师要能充分利用教材素材，明晰数学概念，展开数学“悟”的过程，以课本中的例题、练习题、习题为基础，通过类比、加工改造、加强条件或减弱条件、延伸或扩展，对课本习题进行改编，这样能有效地避免“题海战术”，引导教师远离资料的干扰，减少收集过多教材以外的题目，减轻学生课业负担，以发挥良好的教学导向功能.因此，我们的教学要回归课本，认真研究教材，发挥教材的示范作用.

总之，在新课标理念的指导下，教师可以不拘泥于教材，可以不按教材教学，教师要有独立性，要能根据自己的教学实际情况创造性地使用教材.但在课本例题、习题的教学中，教师首先要对课本例题、习题进行认真分析和研究，为学生参与实践、自主探究、合作交流、阅读自学提供丰富的学习资源，从而帮助学生养成独立思考、积极探索的习惯，让学生在开放的教学环境中培养数学思维品质，发展自己的数学能力.

1.孙红.挖掘教材习题演绎多彩数学——从一道课本经典习题引出的中考题变化［J］.中学数学（下），2014（8）.

2.白军强.教材中一道经典习题在中考中的“多面孔”［J］.中国数学教育（初中版），2009（10）.

3.中华人民共和国教育部.义务教育数学课程标准（2011年版）［S］.北京：北京师范大学出版社，2012.W