多轴机床通用运动学建模方法

李进进 吕学庚

(哈尔滨工业大学机电工程学院，黑龙江 哈尔滨 150001)

刀位文件是用于描述加工过程中刀具运动的中性文件，他包含刀具相对于工件的位置信息和刀轴矢量信息。数控机床无法识别刀位文件，只能识别特定格式的加工代码，加工代码描述的是机床各运动轴的相对运动分量。加工代码具有特异性，一种结构形式的机床只能识别一种特定格式的加工代码。因此，需研究如何将中性的刀位文件转换为机床可识别的加工代码，这个转换过程被称作后处理。后处理的核心是跟据机床的结构形式，建立机床运动学方程，将刀具的位置坐标和刀轴矢量转换成数控机床各直线轴的移动坐标和旋转轴的转角。

Bu P等[1]分别建立工件坐标系及刀具坐标系相对于床身坐标系的坐标变化关系，以床身为参考系的连接点，建立了XYZ-AC式五轴机床运动学模型，并以OpenGL为框架将加工代码转换为刀具的运动轨迹。Lin M T等[2]利用螺旋理论建立了五轴机床运动学方程。Liang Z等[3]借用串联型机器人指数乘积公式建立了五轴机床运动学方程，并利用VC++平台开发了机床后处理程序。She C H等[4]采用坐标变换的方法分别对旋转轴水平正交和旋转轴倾斜的五轴机床建立了运动学方程，并将刀位文件转换成加工代码。Zheng L等[5]将机床运动学方程应用于机床的刀具跟随控制系统中，可简化多轴机床的后处理算法。Wang Feng等[6]分别建立了转台偏置、刀轴偏置、转台刀轴同时偏置的五轴机床运动学模型，并构建了运动学模型库。Chang C等[7]针对主轴电动机在床身，旋转轴倾斜的旋转头式五轴机床，建立了运动学模型，开发了后处理应用程序。Jung.Y.H等[8]研究了倾斜式双转台机床的结构，通过建立机床运动学方程，将加工代码转换为刀具的运动路径，避免刀具发生干涉，实现虚拟仿真加工过程。Anotaipaiboon. W等[9]建立了机床运动学模型，采用数学工具来描述刀尖的运动轨迹，通过优化机床的初始位置减小加工的轨迹误差。

现阶段对于五轴机床运动学建模的研究主要针对某种特定结构的机床，并将运动学方程应用于数控加工的后处理。由于五轴机床的结构类型繁多，对于任意结构的机床，能否采用统一的方法，建立运动学方程并对其进行求解是本文的主要研究内容。本文提出了多轴机床通用运动学建模方法，通过引入边界条件的方式，求解运动学方程，可用于建立各类结构机床运动学模型。

1 数控机床中的坐标系

数控机床中的坐标系主要有3种，分别是机床坐标系、工件坐标系和加工坐标系。机床坐标系符合右手笛卡尔坐标原则，主要用于确定机床各运动部件在机床中的相对位置。工件坐标系又被称作编程坐标系，在进行数控编程时，以工件上某一点为坐标原点建立的坐标系就是工件坐标系，该点被称为工件坐标系的工件原点。刀位文件中刀具的运动信息就是在工件坐标系下确定的。加工坐标系是刀具运动轨迹输出的定位基准。加工坐标系的原点可由工艺员在编译工艺时确定，通常与工件坐标系的原点重合，加工坐标系的坐标轴与机床坐标系的坐标轴重合。

在数控加工时，通过对刀的方式，测量工件坐标系原点与机床坐标系原点间的相对距离，确定工件在机床中的位置坐标。这一距离被称作工件的零点偏置，零点偏置可预先设置在机床控制系统的相关寄存器(G54-G59)中。当机床加工工件时，机床控制系统自动将寄存器中的偏置距离叠加至工件坐标系上，机床控制系统便可按照机床坐标系下的绝对坐标值控制机床各轴的相对运动，实现工件的加工。因此，车间工艺员在数控编程时无须考虑工件在机床中的实际位置，只需按照工件的轮廓形状进行刀具的轨迹规划。机床的运动学方程和后处理也是在工件坐标系下建立的。

2 多轴机床通用运动学建模方法

当机床的运动轴数t≤3时，对于这类低轴机床的运动学方程，由于空间平移运动的齐次坐标变换满足交换律，因此可采用相同形式的机床运动学方程来描述这类低轴机床的运动。针对于任意结构的三轴机床，运动学方程均为公式(1)，各运动轴的依附关系对机床运动学方程没有影响。

(1)

当机床的运动轴数t≥4时，对于这类多轴机床的运动学方程，由于空间旋转运动的齐次坐标变换不满足交换律，因此无法采用如公式(1)所示的运动学方程进行描述，需要针对不同结构形式的机床，建立不同的机床运动学方程，来描述刀具坐标系与工件坐标系间的相对运动关系。

由于机床的运动形式与其他机械结构的运动形式存在明显区别，在研究机床的运动时，更关注刀具相对于工作台的位置及姿态的变化，尤其是针对多轴机床来说，这是两个非惯性系间的坐标变换。传统的机械结构，例如，当建立机器人结构的运动学方程时，则是通过在相对静止的零号杆件(即机座)上建立惯性参考系来研究末端执行机构的位置及姿态的变化。当建立机床的运动学方程时，以工作台为零号部件，按照运动轴的依附关系将各运动轴依次连接，将机床视为串联型结构，床身视为相对运动部件，刀具视为最末端的执行机构。通过建立相邻运动部件间的坐标变换关系，建立刀具相对于工作台的机床运动学方程。

坐标变换是指采用数学方法将空间中一个坐标系下的点或矢量，通过变换得到其在另一个坐标系下坐标的过程。齐次坐标变换矩阵是实现齐次坐标变换的重要数学工具。因此，在进行多轴机床运动学建模时，首先需要为机床中的每个运动部件建立局部坐标系，每个坐标系均符合右手笛卡尔坐标系规则，且坐标轴的方向统一，每个局部坐标系表示一个运动部件，采用4×4阶齐次坐标方阵表示相邻部件间的运动关系。

3 多轴机床通用运动学建模步骤

步骤1 部件编号

根据机床结构划分运动部件，依据各运动部件间的依附关系，将包括机床床身在内的各运动部件(床身视为相对运动部件)，从工作台至刀具进行由0依次递增地编号κ。对于通用运动学建模方法，无论旋转轴在哪一端(工件端或者刀具端)，可先分别假设旋转轴在两端同时存在，在工件端的第一旋转轴局部坐标系为RCSw1，第二旋转轴的局部坐标系为RCSw2；在刀具端第一旋转轴的局部坐标系为RCSt1，第二旋转轴的局部坐标系为RCSt2。从工作台到刀具的多轴机床通用坐标变换矩阵可表示成如下的形式：

WCS→RCSw2→RCSw1→XCS→YCS→MCS→

ZCS→RCSt1→RCSt2→TCS

式中：WCS为工作台的局部坐标系；XCS为直线轴X轴的局部坐标系；YCS为直线轴Y轴的局部坐标系；ZCS为直线轴Z轴的局部坐标系；MCS为机床床身的局部坐标系；TCS为刀具的局部坐标系。其中，工作台坐标系WCS的编号κ=0，各运动轴的编号依次递增，床身坐标系MCS的编号κMCS=5，刀具坐标系TCS的编号为κ=9。

步骤2 确定矩阵符号

根据编号，计算各运动轴的矩阵符号，矩阵符号的计算函数为

(2)

式中:λ=κ-κMCS，物理意义为比较运动部件在机床中的相对位置关系，以机床床身坐标系为基准，若运动部件靠近工作台端，则根据运动部件的性质(直线运动或旋转运动)作相应齐次坐标变换的逆变换；若运动部件靠近刀具端，则作相应齐次坐标变换的正变换。

步骤3 建立齐次坐标矩阵

根据各运动部件的运动性质，建立相邻运动部件间的齐次坐标变换矩阵

WTT=WTRw2·Rw2TRw1·Rw1TX·XTY·
YTM·MTZ·ZTRt1·Rt1TRt2Rt2TT

(3)

式中：iTi+1为运动部件i+1相对于运动部件i的齐次坐标变换矩阵。

在进行特定机床运动学建模分析时，可将通用运动学建模过程中不存在的旋转轴齐次坐标变换矩阵归约为单位阵。

步骤4 匹配矩阵系数

根据公式(2)确定的各运动部件矩阵符号系数，将各运动部件的齐次坐标变换矩阵同其矩阵符号系数相匹配，如公式(4)。

(4)

步骤5 平移矩阵融合

(5)

公式(5)称为通用机床的形状函数。

步骤6 计算运动学方程

将通用机床的形状函数左乘刀具坐标系的齐次坐标变换矩阵，获得刀具在工件坐标系下的位置及姿态坐标，即运动学方程

(6)

式中：Kx、Ky、Kz分别为在工件坐标系下的刀轴矢量与各坐标轴的方向余弦；Qx、Qy、Qz分别为工件坐标系下刀具的位置坐标。

步骤7 定义并引入边界条件

将机床各转动轴转角φ1和φ2至零，此时工件坐标系下的刀具位置坐标与加工代码中各直线轴的运动分量相等，以此作为运动学方程求解的边界条件。

当φ1=φ2=0时[QxQyQz1]T=[XYZ1]T

(7)

将公式(7)代入公式(6)求得刀具相对于工作台的综合坐标变换矩阵中的各项移动系数。

步骤8 求运动学方程逆解

将移动系数Px、Py、Pz代入公式(6)，根据矩阵元素对应相等原则得运动学方程逆解

步骤9 求运动学方程正解

联立运动学方程逆解，求得运动方程正解

4 仿真与验证

利用上文所述的多轴机床通用运动学建模方法，求解如图1所示的一种XYZ-BC式摆头转台五轴机床运动学方程。并将某一型号精锻叶片进气缘处的铣削精加工刀位文件转换成数控加工代码。在VERICUT仿真平台中搭建虚拟仿真机床，进行铣削仿真验证。

在图1中，B轴为摇摆轴，可使机床主轴绕Y轴摇摆。C为旋转轴，可使工作台绕Z轴旋转。分别在刀具端建立刀具坐标系、工件端建立工件坐标系，并以刀具坐标系Y轴为轴心建立旋转轴B轴的旋转坐标系，以工件坐标系Z轴为轴心建立旋转轴C轴的旋转坐标系。

根据前文所述的建模方法，两个旋转轴分别在刀具端和工件端，根据旋转轴的位置，将两个旋转轴的旋转齐次坐标变换矩阵带入通用运动学方程中，并将刀具端和工件端多余的旋转齐次坐标变换矩阵归约为单位阵，则摆头转台式五轴机床的运动学形状函数为：

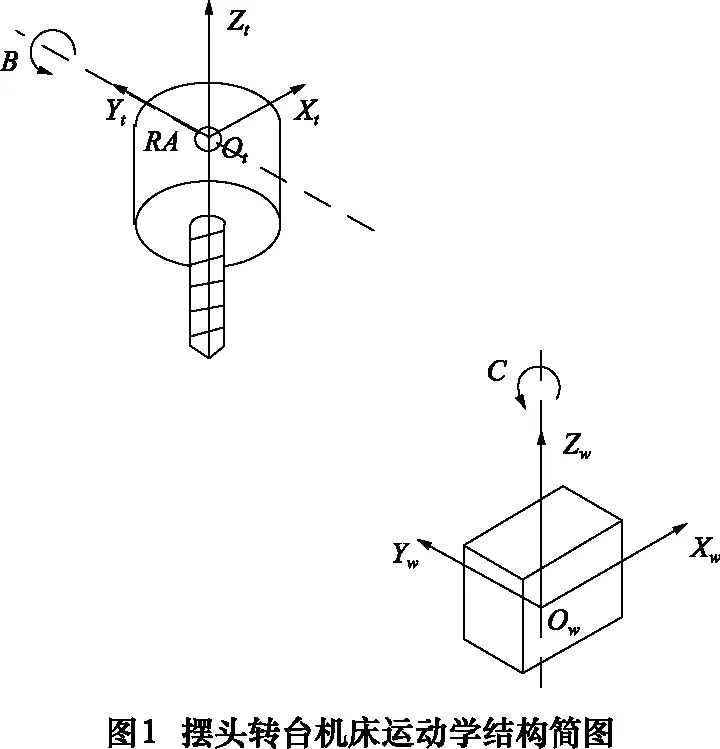
对于图1所示的摆头转台机床，将φy=B、φz=C带入运动学形状函数得机床运动学方程的通解：

(8)

根据边界条件的定义，当B=C=0时：

[QxQyQz1]T=[X Y Z 1]T=[PxPyPz1]T

(9)

将边界条件(9)带入运动学方程通解(8)得运动学方程特解为：

(10)

运动学方程的逆解可由运动学方程(10)矩阵元素对应相等原则得出：

运动学逆解可用于将加工代码转换为刀位文件，即反后处理过程。

通过联立运动学逆解，求得运动学正解为：

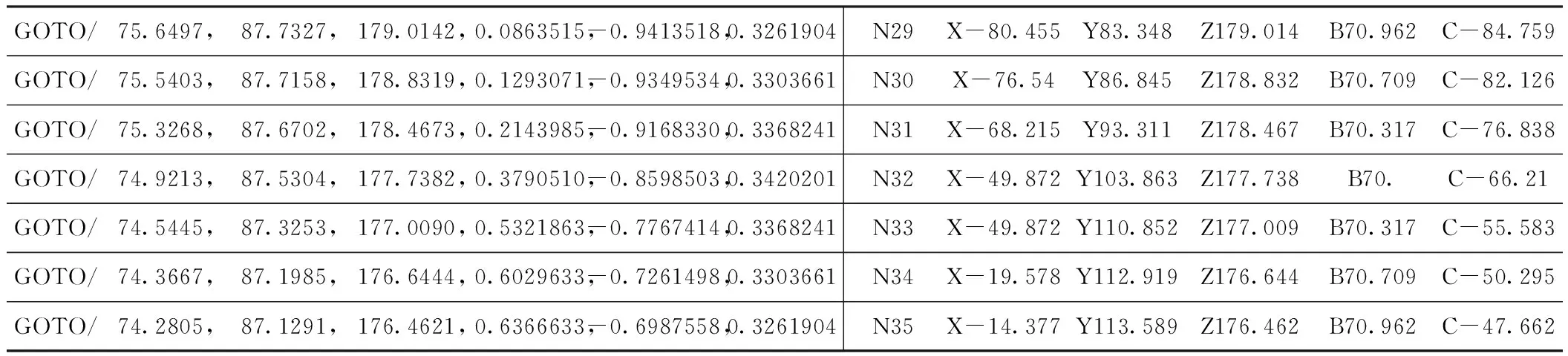
表1 叶片进气缘的铣削加工刀具路径和转换后的加工代码

GOTO/75.6497,87.7327,179.0142,0.0863515,-0.9413518,0.3261904N29X-80.455Y83.348Z179.014B70.962C-84.759GOTO/75.5403,87.7158,178.8319,0.1293071,-0.9349534,0.3303661N30X-76.54Y86.845Z178.832B70.709C-82.126GOTO/75.3268,87.6702,178.4673,0.2143985,-0.9168330,0.3368241N31X-68.215Y93.311Z178.467B70.317C-76.838GOTO/74.9213,87.5304,177.7382,0.3790510,-0.8598503,0.3420201N32X-49.872Y103.863Z177.738B70.C-66.21GOTO/74.5445,87.3253,177.0090,0.5321863,-0.7767414,0.3368241N33X-49.872Y110.852Z177.009B70.317C-55.583GOTO/74.3667,87.1985,176.6444,0.6029633,-0.7261498,0.3303661N34X-19.578Y112.919Z176.644B70.709C-50.295GOTO/74.2805,87.1291,176.4621,0.6366633,-0.6987558,0.3261904N35X-14.377Y113.589Z176.462B70.962C-47.662

运动学逆解可用于将刀位文件转换为加工代码，即后处理过程。

运用运动学方程的正解，将精锻叶片进气缘处精加工刀位文件中刀具位置坐标和刀轴矢量夹角转换为摆头转台式数控机床各移动轴运动分量和各转动轴转角，部分代码的转换结果如表1所示。

在VERICUT仿真平台中搭建XYZ-BC式摆头转台五轴机床，如图2所示。

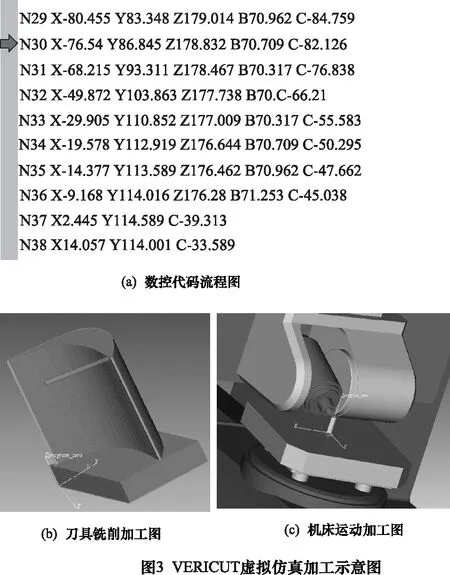
采用Fanuc-30i数控系统进行虚拟仿真加工，加工代码的运行过程如图3a所示，当数控程序运行至N30行时，刀具的加工过程如图3b及机床各运动部件的相对位置如图3c所示。

通过虚拟仿真加工过程可以看出，由摆头转台式五轴机床运动学正解转换得到的数控加工代码满足加工要求。因此，验证了多轴机床通用运动学建模方法的正确性。

5 结语

(1)为提出适用于各类多轴机床的通用运动学建模方法，首先将多轴机床视为同时具备四个旋转轴的串联型机构，通过采用对各运动部件编号及排序的方法，确定相邻部件齐次坐标变换的方向性。

(2)为解决移动坐标系原点不重合导致运动学建模困难的问题，提出了平移齐次坐标变换矩阵融合的方法，将3个平移矩阵转换为刀具相对于工作台的综合移动矩阵，建立机床的通用运动学形状函数。

(3)为提高求解运动学方程的准确性，定义了求解运动学方程的边界条件。当各转动轴转角为零时，刀位文件中的刀具位置坐标与加工代码中各移动轴运动分量相等。边界条件适用于任何复杂结构机床运动学方程的求解。

(4)通过本文提出的通用运动学建模方法建立了XYZ-BC式摆头转台五轴机床运动学方程，并将铣削精锻叶片进气缘处的刀位文件转换为加工代码，通过VERICUT仿真平台搭建虚拟机床，进行仿真加工，验证了多轴机床通用运动学建模方法的正确性。

[1] Bu P, Li J, Huang L. A general motion simulation description of multi-axis CNC machine tools[C]// Control Conference. 2012:4486-4489.

[2] Lin M T, Lee M C, Lee J C, et al. A look-ahead interpolator with curve fitting algorithm for five-axis tool path[C]// IEEE International Conference on Advanced Intelligent Mechatronics. IEEE, 2016:189-194.

[3] Liang Z, Li J, Lou Y, et al. A unified framework of postprocessor for multi-axis machine tools[C]// International Conference on Digital Manufacturing & Automation. IEEE Computer Society, 2010:152-155.

[4] She C H, Huang Z T. Postprocessor development of a five-axis machine tool with nutating head and table configuration[J]. The International Journal of Advanced Manufacturing Technology, 2008, 38(7):728-740.

[5] Zheng L, Hu L, Feng W, et al. Integration of the five-axis tool center point control function in CNC system[C]// Industrial Electronics and Applications. IEEE, 2010:439-444.

[6] Wang Feng, Lin Hu, Zheng Liao mo, et al. Design and implementation of five-axis transformation function in CNC system[J]. Chinese Journal of Aeronautics, 2014, 27(2):425-437.

[7] She C H, Chang C C. Development of a five-axis postprocessor system with a nutating head[J]. Journal of Materials Processing Technology, 2007, 187-188(12):60-64.

[8] Jung Y H, Lee D W, Kim J S, et al. NC post-processor for 5-axis milling machine of table-rotating/tilting type[J]. Journal of Materials Processing Technology, 2002, 130(2):641-646.

[9] Anotaipaiboon W, Makhanov S S, Bohez E L J. Optimal setup for five-axis machining[J]. International Journal of Machine Tools & Manufacture, 2006, 46(9):964-977.