基于细菌觅食算法的自适应NURBS曲线插补*
谷 岩 周 岩 林洁琼 曹东旭 刘 阳 孙彦东
(长春工业大学机电工程学院, 吉林 长春 130012)
随着制造行业的不断发展,自由型曲线曲面加工所采用的直线和圆弧逼近的传统方法已经无法满足现阶段对加工件的加工精度及加工效率的要求,近年来,多位学者对NURBS曲线插补方法进行了深入探究,如沈洪垚提出了基于节点组合优化策略的刀路曲线拟合方法研究[1],提高了NURBS曲线的加工精度;罗福源等提出了NURBS曲线S形加减速双向寻优插补算法研究[2],对速度进行相应规划,使得曲线过渡更为平滑;在实际加工过程中,一些学者利用智能算法对速度和路径进行重新规划,以获得更优解[3]。本文在现有理论基础上,提出利用细菌觅食算法优化NURBS曲线的控制点变量个数及关键位置信息,调整曲线参数使其得到最优解,减小计算载荷,并通过对速度关键点进行S型加减速规划控制,可使得曲线加工速度保持最佳,加工过程平稳无波动,从而达到高效高精加工的要求。
1 NURBS曲线规划
1.1 NURBS曲线定义
在参数化曲线表示形式中,一条三次NURBS曲线可以表述为:
C(u)=(x(u),y(u),z(u))
(1)
其中u为任意值,0≤u≤1。
将曲线转化为参数形式对于机床多轴控制非常方便,通常可以通过参数方程单独驱动每一轴的运动。因此为了实现多轴联动,我们可以将等式扩展为p次NURBS参数方程。
确定p次NURBS曲线C(u)的表示方法为:
(2)
式中,节点矢量U={u0,u1,…un-p+1},控制顶点P={P0,P1,…Pn}、权重因子w={w0,w1…wn},定义Ni,p(u)为P阶基函数,其定义需满足以下要求:
(3)
(4)
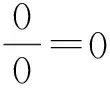
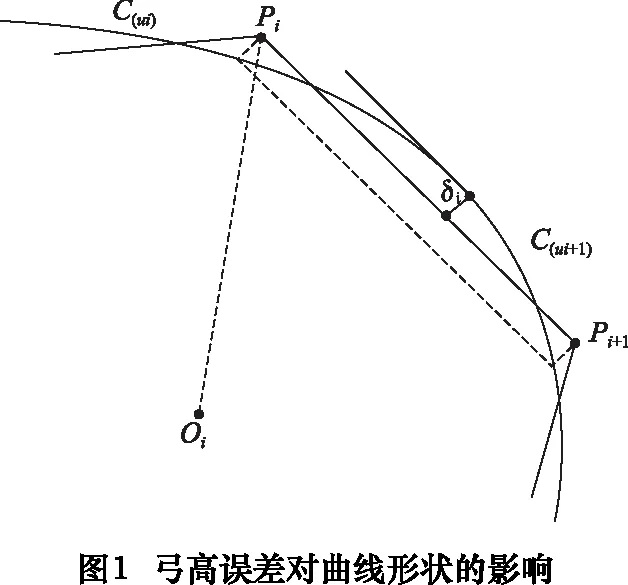
1.2 弓高误差的计算
弓高误差被认为是影响加工精度的关键因素,也是用来判定曲线加工精度的重要参数,在数控插补时,可以利用曲率半径来限制弓高误差[4],用弦线段对两相邻插补点间的弧段进行逼近来实现对参数曲线运动轨迹控制,这种逼近将会带来插补弓高误差[5](如图1),因此需要通过规划合理刀具路径及速度来减小弓高误差,提高加工精度。将插补点C(u)处的微弧段近似于圆弧处理,由几何知识可知,曲线曲率ρ、进给速度Vi、插补周期T以及最大限制插补弓高误差δmax之间满足下式:
(5)
2 细菌觅食算法优化NURBS曲线
2.1 细菌觅食算法(BFO)综述
细菌觅食算法是一种新的生物启发优化算法,该算法可以解决非线性、多维的全局性优化问题[6]。由式(2)和式(4)可知,若想优化NURBS曲线,可以通过优化控制顶点和权重因子来实现,而权重值的优化过程复杂而繁琐。为方便深入探究,本文利用细菌觅食算法优化控制点的参数值及变量个数,以优化NURBS轨迹,减小计算负荷。
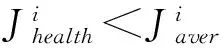
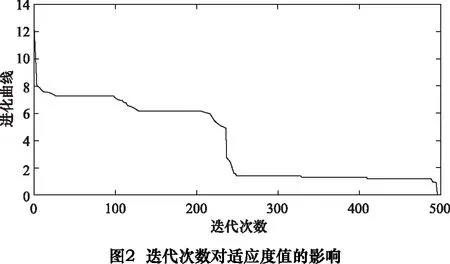
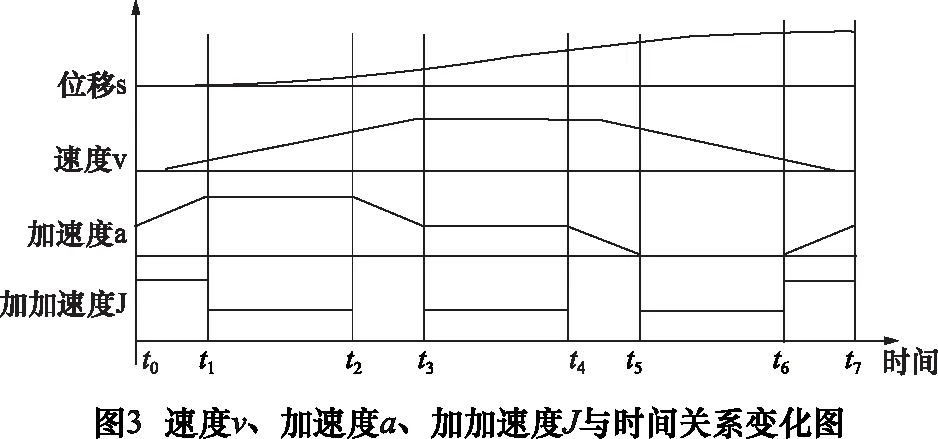
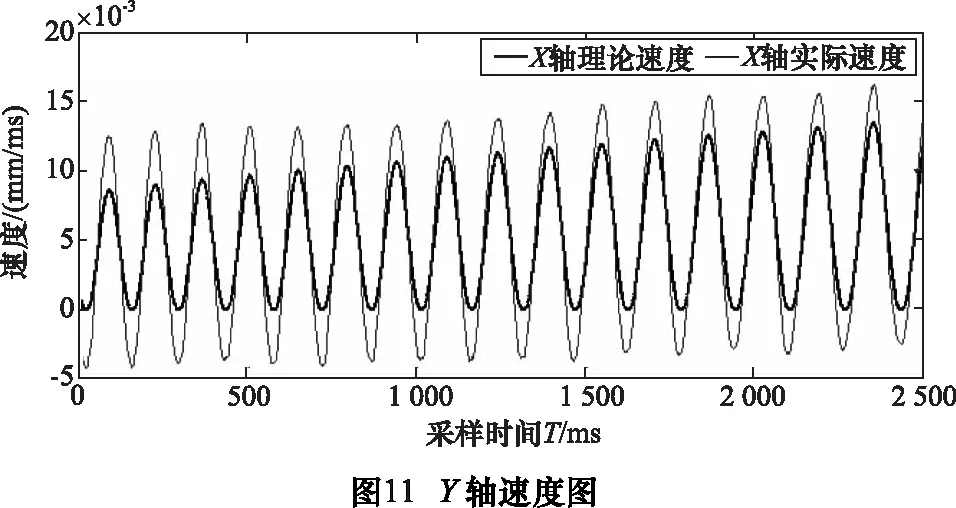
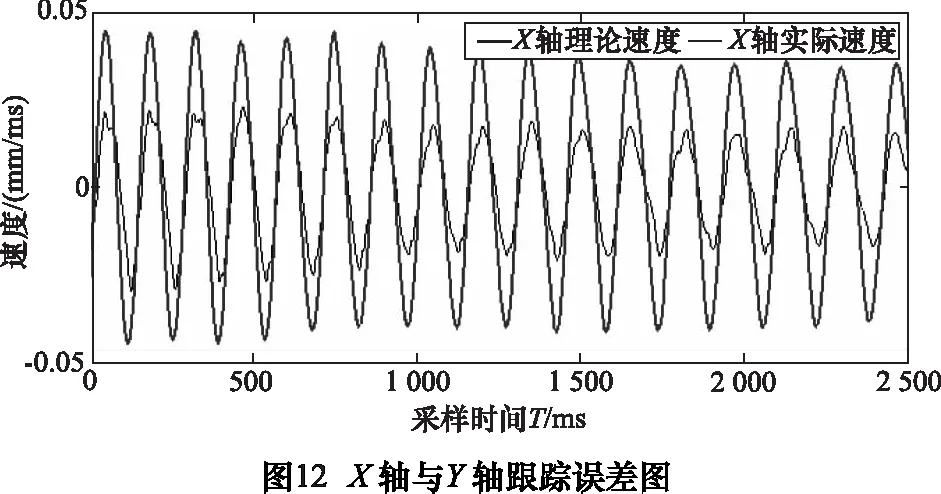
为了便于BFO直接参与曲线插补,引入适应度函数概念,使BFO模型操作结果与NURBS控制点建立函数关系。首先创建Pn组控制点,每组控制点对应的权重值w(0 由式(2)可知,NURBS曲线的pu值可得: (6) 为了降低NURBS求导的计算复杂度[7],便于构造适应度函数,本文将NURBS曲线改写为矩阵形式: (7) (8) 通过式(7)、(8)可将NURBS描述为: (9) 其中:P为有序数据点集矩阵;W(u)为NURBS曲线基函数。可得出曲线控制点C的近似解: C=(ATA)-1ATP (10) 代入式(2)可得到矩阵形式参数拟合曲线: C(u)=A(ATA)-1ATP (11) 记Cj(u) 为拟合曲线上对应参数tj的点,则误差平方和为: (12) 结合式(4),可导出适应度函数公式: (13) 其中,k为搜索半径的倒数。构造函数关系后,需要对Err及Pn两个参数进行整体优化,开始进行算法优化操作。 (1)趋向性操作 在BFO 模型中,细菌的趋向性操作的数学表达式为: (14) 将大肠杆菌觅食的特性抽象为数学模型,为提高稳定性,采用间隔法选取优化点,并保留初始点P0和终止点Pn,计算每两个相隔控制点的函数适应度值,并比较结果决定是否保留原有值或使用新值替换原有值。 (2)繁殖性操作 (15) (3)迁移性操作 (4)聚集性操作 此处聚集性操作为可选性操作,前文提到在曲率变化较小的位置采用迁移性操作以减少计算程度,而为了使得误差进一步缩小,可以选用聚集性操作,参数优值会在曲率变化较大处密化,此种方式可在增加部分计算的情况下获得更优解。 (5)算法检验 根据BFO算法进行迭代,并通过式(14)进行检验,可得出结论当迭代次数为496次时接近最优(如图2)。为更加确定优化结果,本文控制点数量为500个。 在曲线插补过程中,最大速度不能超过机床限制速度,最大误差不能超过弓高误差[8],故有公式: (16) 整段加工过程需要满足机床动力学约束条件: (17) 通常根据曲线曲率极值点进行分段,对该段内速度进行探究,发现部分速度点虽满足误差要求,但在曲线拐点处(即曲线曲率极值点处)速度变化明显,加速度ai及加加速度Ji无法满足机床最大承载能力,故需要对速度进行重新规划,以满足机床约束。 由3.1节知,曲线速度规划仅在曲率变化较大时不满足要求。为使得加工过程速度平稳变化,减小速度波动,本文采用七段式S型加减速对速度进行规划: 将加减速的过程分为七段:加加速阶段(t0-t1)、匀加速阶段(t1-t2)、减加速阶段(t2-t3)、匀速段(t3-t4)、加减速阶段(t4-t5)、匀减速阶段(t5-t6)、减减速阶段(t6-t7)。当曲线曲率较小时,设加加速度Ji=Jmax,则可知各阶段速度、加速度如表1。 表1 七段速度规划表 ztJ(t)a(t)V(t)S(t)10≤t≤t1J1J1t1V1+12J1t12V1t1+12J1t132t1≤t≤t20AVt1+At2St1+V1t2-12At223t2tt3J3A-J3t3Vt2+At3-12J3t32St2+V3t3-12At32-16J3t334t3tt400Vt3≡Vt4≡VcSt3+V3t45t4tt5J5-J5t5Vt4+12J5t52St4+V4t5-16J5t536t5tt60-DVt5-Dt6St5+V5t6-12Dt627t6tt7J7-D+J7t72Vt6-Dt7+12J7t72St6+V6t7-12Dt72-16J7t73 根据表1所示的规划方法,可得到对应速度曲线,如图3。 由图知:此种方法可以满足速度的平滑连续变化,与直线三段式加减速规划法相比加工过程更为平稳,减小了速度和加速度突变,与指数曲线加减速规划法相比,加工所需规划时间短,效率更高,可以适用于高精高速加工及柔性制造。 在实际加工中,存在加加速度满足而速度超限的情况,故需要对速度进行检验,通过以下几步骤: (1)设vi为速度最大点,即当vi=vmax时,将该点与机床限定最大值vlimit进行比较。 (2)若vi>vlimit,则在vi-1处提前结束加速过程,并将加加速度J调整为最小值Ji=Jmin。 (3)检测vi和vi+1是否满足要求,若满足,则令J=0,继续速度规划,若不满足,重复步骤(2),直至符合要求。 (4)结束速度规划检测程序。 为了验证本文提出优化算法的可行性,本文采用复杂的蝴蝶形曲线加以仿真及实验验证。 仿真软件采用MATHWORKS公司提供的MATLAB软件,此软件可处理相应的曲线参数,工作平台选用Pentium©Dual-Core E5300,内存为2GB,经过仿真得出参数曲线(如图4)。 同时对预先规划的实时速度进行拟合,得出X轴参数u与速度v的关系(如图5)。 同理可得Y轴参数u与速度v的关系(如图6)。 为验证此方法实际可行,进行实验加工加以验证(图7)。实验平台选用五轴精密抛光机床,控制器采用AEROTECH公司的A3200纯软件控制器,实验刀具采用威特N3J62501(φ0.1 mm)尖刻刀,采用一步连续加工方式,对上述方法加以验证(图8)。 通过A3200中的Digital Scope模块对加工过程参数进行采集,得到实验各项参数,通过对急转角局部采样数据进行分析,得到图9~12所示参数图像。 从图9看出X轴的实际速度与其理论速度存在误差,但大体走势与预期的基本相同且在误差允许范围内。图10是其局部放大图,由于机床震颤产生较大速度波动。图11中的速度大体趋势与X轴相同且比X轴更加平稳,这点由图12中的跟踪误差可以看出。在图12中X轴的跟踪误差明显大于Y轴的,由于误差在允许范围内,验证速度规划是正确的。 (1)本文利用细菌觅食算法对NURBS曲线的控制点数量及关键位置信息进行优化,分别经过趋向性操作、繁殖性操作、迁移性操作以及可选择的聚集性操作对控制点数量及位置进行调整,并利用曲线弓高误差对曲线关键位置信息进行检验及调整,从而得到最优解,构造出平滑曲线,并减小了计算负荷,使得算法优化实时在线加工成为可能。 (2)本文通过确定加减速关键点,在急转角进行速度规划,在误差及机床限制范围内得到最优速度,并通过S型加减速对加速度变化过大段进行重新规划,保证了速度的平滑连续变化,比直线三段式加减速规划法更加平稳,比指数曲线加减速规划法效率更高,本文通过对蝴蝶型曲线进行仿真以及实验验证,保证最优速度在限制范围内前提下,提高了加工精度。从实验中采集的数据可以看到误差在允许范围内,证实了本文优化算法的可行性。 [1]沈洪垚. 自适应NURBS曲线插补关键技术及实现研究[D]. 杭州:浙江大学, 2010. [2] 罗福源, 游有鹏, 尹涓. NURBS曲线S形加减速双向寻优插补算法研究[J]. 机械工程学报, 2012, 48(5):147-156. [3] 孙越泓, 魏建香, 夏德深. 基于自适应遗传算法的B样条曲线拟合的参数优化[J]. 计算机应用, 2010, 30(7):1878-1882. [4] 刘献礼, 周肖阳, 李茂月,等. NURBS曲线S形加减速寻回实时插补算法[J]. 机械工程学报, 2017, 53(3):183-192. [5] 魏栋. 面向复杂曲面加工的NURBS曲线逼近及插补算法研究[D]. 杭州:浙江大学, 2017. [6] 李珺, 党建武. 改进细菌觅食算法在高维优化问题中的应用[J]. 计算机科学, 2017, 44(4):269-274. [7] 蔡安江, 杜金健, 宋仁杰,等. 五轴加工刀具轨迹NURBS插补技术的研究[J]. 机械科学与技术, 2017, 36(3):402-408. [8] Lu L, Zhang L, Gu Y, et al. Fast parametric curve interpolation with minimal feedrate fluctuation by cubic B-spline[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2016: 0954405416673680. [9] 卢磊. 自由曲面加工速度规划与插补算法研究[D].长春: 吉林大学, 2016. [10]Passino K M. Biomimicry of bacterial foraging for distributed optimization and control[J]. IEEE Control Systems, 2002, 22(3):52-67.
1.4 细菌觅食算法优化实现

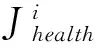
3 NURBS曲线速度自适应插补
3.1 NURBS曲线插补速度规划
3.2 速度重规划——S型加减速研究

3.3 速度规划设计
4 仿真及实验
4.1 仿真

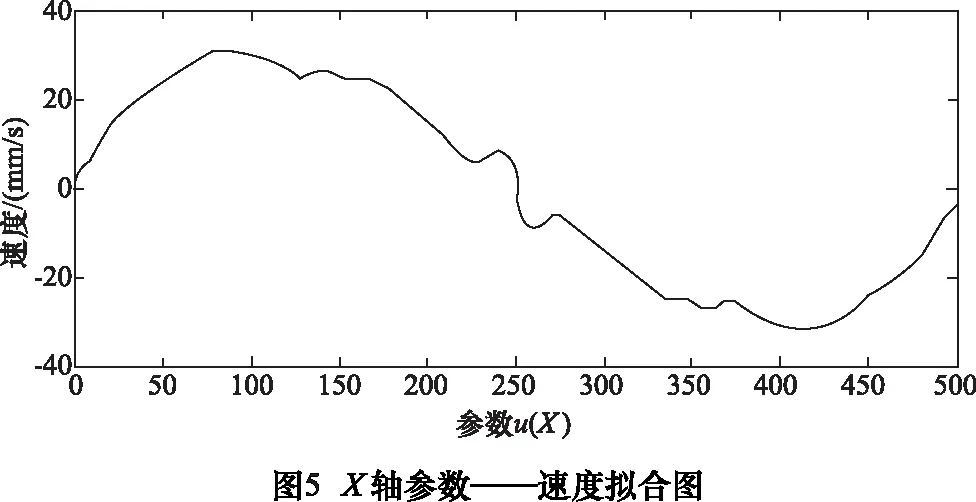
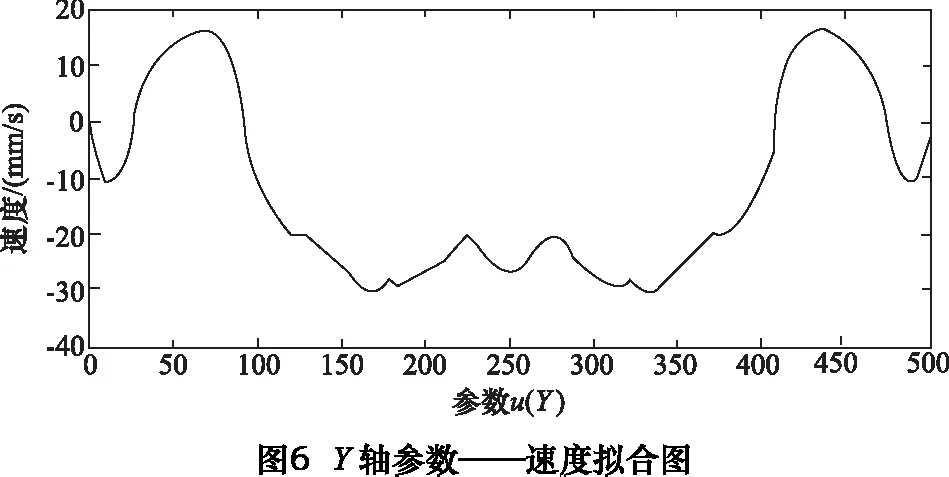
4.2 实验验证


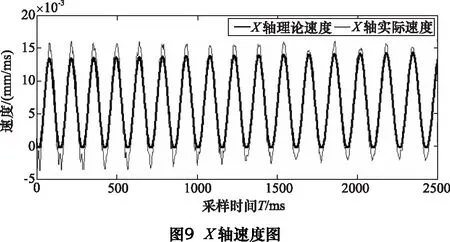
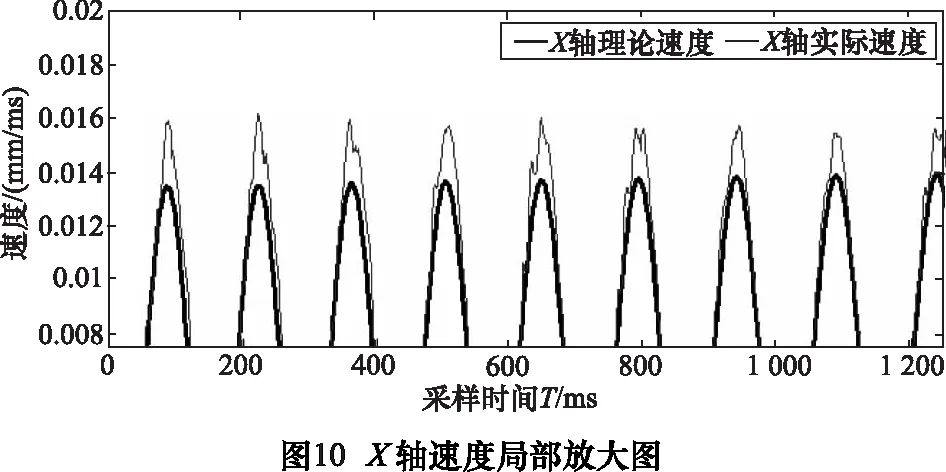
5 结语

