单向相关下的机械零件动态可靠性分析

杨 娜

(兰州职业技术学院机电工程系, 甘肃 兰州 730000 )

应力-强度干涉模型是机械可靠性分析的理论基础，其中的应力和强度都是广义的概念，即广义应力是载荷、振动、温度、噪声、腐蚀等所有可能导致零部件破坏的因素，属于外部特性；广义强度是零部件能够抵抗破坏的能力，属于内部特性。但传统的应力-强度干涉模型存在两方面的不足：(1)通常将应力与强度视为两个随机变量，未考虑其随时间的变化，由此得到的是静态的可靠度；(2)往往假设应力与强度之间相互独立。而实际上，应力与强度间存在相关性，随着载荷的作用，强度会逐渐降低。机械零部件在运行过程中，由于受载荷、振动、温度、辐射、噪声、腐蚀等外部环境及其自身材料缺陷、老化、分散性等综合影响，其实际工作情况下的应力与强度是不确定的，是随时间变化的随机变量，即为随机过程。因此，应力-强度干涉(stress-strength interference，SSI)过程应是一个动态过程，相应的可靠度也就是随时间变化的函数。

随着机械系统和工作环境日益复杂化，产品的性能和可靠性需要满足更高的要求。对于机械零件的可靠性预测问题，国内外大量学者进行了相关研究。动态与渐变是机械产品不可避免的随时间变化的形态，对机械产品进行动态与渐变可靠性探究是可靠性研究的递进与升华[1]。文献[2]运用顺序统计量理论以及基于独立的SSI模型，建立了以载荷作用次数为寿命度量指标的零件动态可靠度计算模型。文献[3]建立了不确定性载荷作用下的零件时变可靠性模型，给出了基于载荷和强度分布的零件可靠度计算表达式。文献[4]基于结构抗力与载荷效应相互独立的基本假设，提出了考虑结构动态可靠性的全随机过程模型。文献[5]分析稳定应力和冲击应力组成的复合应力，推导了考虑强度退化时的可靠性模型。上述模型虽然研究的是动态可靠性问题，但大多立足于应力与强度相互独立的假设，因此，对于应力与强度间的相关性的描述存在明显不足。文献[6]考虑组合应力下的结构受力情形，分别探讨了强度退化与否的动态可靠度。文献[7]考虑随机载荷的加载形式分别为动载荷累加、等幅并且服从Poisson分布、载荷随时间变化且不服从任何分布的三种情况，利用应力-强度干涉理论和随机过程理论建立了结构强度退化情况下的动态可靠性模型。文献[8]考虑载荷随时间变化及强度退化，运用随机过程和顺序统计理论，建立变幅随机载荷和强度退化下零件的动态可靠性模型。文献[9]通过定义次数等效系数和参考载荷，分析随机载荷作用下强度发生退化，推导了存在共因失效的零件可靠度计算模型。上述文献在一定程度上分析了载荷与强度的相关性，但其相关性多基于文献[10]所提出的剩余强度模型来体现。在工程实际中，零部件的强度在不同的应力水平下会有不同的表现，也就是说强度与应力是单向相关的。所谓应力与强度单向相关，是指强度受应力特性的影响，并随应力的作用逐渐降低，而应力则取决于外部载荷和工作环境，与强度无关。

为评估零件在应力与强度单向相关下的动态可靠度，本文利用Gamma过程来描述随机载荷作用，基于经典的Miner累积损伤理论，进一步推导随着载荷作用而产生的强度不断降低的强度退化模型。结合传统的应力-强度干涉模型，建立零件的动态可靠度预测模型。最后通过算例验证模型的有效性。

1 传统的应力-强度干涉模型

传统的应力-强度干涉模型把应力与强度作为两个随机变量，若使零部件正常工作，则要求其强度大于工作应力，否则零部件将遭到破坏。应力和强度都应该是广义的概念，广义应力是载荷、振动、温度、噪声、腐蚀等所有可能导致零部件破坏的因素，属于外部特性；广义强度是零部件的抗热性、耐磨性、抗腐蚀性等能够抵抗破坏的能力，属于内部特性。可靠度R则是零部件强度δ大于应力s的概率P，可以表达为：

R=P(δ>s)

(1)

将应力与强度作为两个随机变量，可以把式(1)作如下表达[11]：

(2)

式中：f(s)表示应力s的概率密度函数；g(δ)表示强度δ的概率密度函数。

上述模型是一个静态模型，不能直接应用于当应力与强度随时间变化的情况。而事实上，由于影响零件性能的外部环境因素是动态的随机过程，应力与强度在很多情况下是随时间变化的，即应力与强度均应为随机过程。

2 动态可靠性分析

2.1 随机载荷的描述

Gamma过程增量具有非负的单调性，多用于描述不可逆转的单调变化的随机过程。在描述载荷、温度、磨损、腐蚀等方面得到了广泛应用。在加速寿命试验中，为减少试验时间，常采用增加载荷的方法，Gamma过程在此类可靠性试验中也得到了广泛运用。

称随机过程{X(t),t≥0}服从形状参数为a(t)、尺度参数为b的Gamma过程，如果其满足下列条件：

(1)X(0)=0；

(2)X(t)在非相交的区间具有独立增量X(t)-X(s)(t>s≥0)；

(3)对任意t>s≥0，有增量X(t)-X(s)～Ga(a(t)-a(t),b)。

其中：Ga(·)表示Gamma分布，a(t)和b分别为形状参数和尺度参数，且a(t)为递增的连续函数，a(0)=0，b>0。当a(t)为现象函数时，Gamma过程为平稳过程；当a(t)为非线性函数时，Gamma过程为非平稳过程。设X(t)为零件t时刻承受的载荷，则其概率密度函数为：

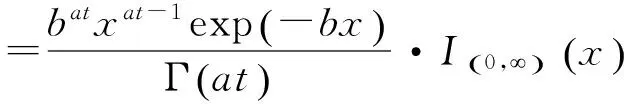
(3)

式中：Γ(·)表示Gamma函数，即：

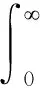
(4)

IA(x)为示性函数；当x∈A时，有IA(x)=1，若x∉A时，有IA(x)=0。由平稳增量的性质可知，在任意时刻t，随机过程X(t)的数学期望和方差将随时间呈线性增长的趋势，则有下列表达式：

μX(t)=at/b

(5)

(6)

2.2 随机载荷下的强度退化模型

材料的疲劳性能通常用其承受的应力s与失效时的应力循环次数N之间的关系来描述，即经典疲劳强度理论中的s-N曲线。在s-N曲线上，对应于寿命N时的应力值，称为材料寿命为N时的疲劳强度。因此，s-N曲线也称为疲劳强度-寿命曲线。s-N曲线反映的另一种信息是：随着载荷作用次数的增加，材料强度在逐渐降低。

s-N曲线通常用幂函数表示，即零件疲劳性能曲线满足下式[12]：

smN=C

(7)

式中：m、C为与材料性质有关的常数，N为载荷s作用下的零件寿命。

由式(6)可知，当应力s作用时，零件的寿命为N。由Miner累积损伤理论，应力s作用时对零件造成的损伤为1/N，即有1/N=sm/C。

假设零件在某随机载荷s(t)作用下工作，则由式(6)可得到：

(8)

零件在经时间t之后，其累积损伤D(t)为：

(9)

零件在下一时刻t+Δt载荷作用时不发生失效，则要求：

(10)

考虑零件的安全性，式(10)右端可设为一个小于1的数，受多种因素的影响，该值实际上为分布在1附近的随机变量。为简化讨论，这里取为常数1。将式(8)代入式(9)并化简得：

(11)

所以，在经历载荷作用时间t之后，零件能够抵抗的临界载荷S(t)为：

(12)

在初始时刻，即t=0时，由式(12)可知s(0)=C1/m。从广义上来说，临界载荷可以称为强度。式(11)即是随机载荷下的剩余强度模型，该式表明，随着载荷作用时间的增加，零件强度逐渐降低，也就表现了载荷与强度之间的单向相关性。

3 单向相关下的动态可靠性模型

早期对可靠度的计算多采用强度与应力相独立的假设，以此得到的结果与工程实际有一定的偏差。实际上在应力作用的过程中，强度通常会逐渐降低，即强度与应力是相关的。这与事实相符合，也得到了大量实验的验证。零部件的强度往往受到应力的影响，在不同的应力条件下表现出不同的特性，而应力则取决于载荷、工况等外部环境，与强度无关。因此，强度与应力表现为一种单向相关的现象。

上文利用Gamma过程对随机载荷进行了描述，并由Miner损伤累积建立了随机载荷下的零件强度退化模型。根据应力-强度干涉模型，零件在任意时刻的动态可靠度函数可以表示为：

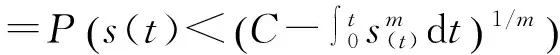
(13)

式(13)即为应力与强度单向相关下的零件动态可靠度模型。

4 算例分析

为对本文方法的有效性进行验证，在此以文献[13]中提供的风电叶片复合材料疲劳试验数据为例。试样材料为单向碳/环氧复合材料，在瑞士产AMSLER 10HFP1-478高频疲劳试验机上进行轴向拉-拉加载疲劳试验，疲劳试验数据如表1所示。

表1 疲劳试验数据

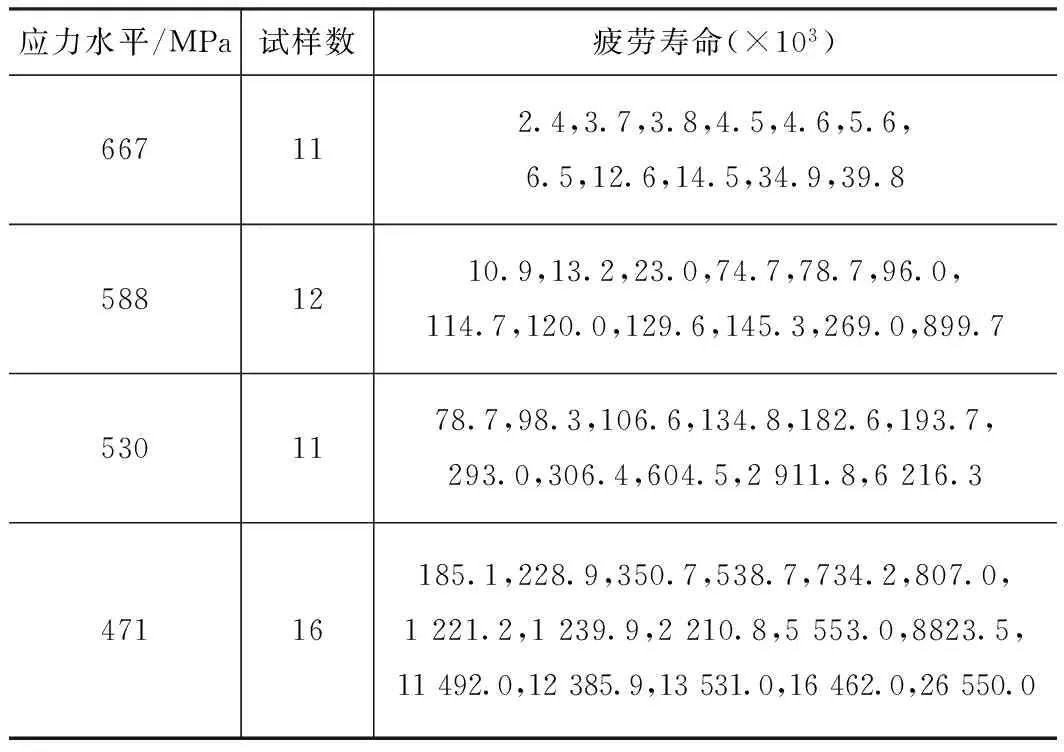
应力水平/MPa试样数疲劳寿命(×103)667112.4,3.7,3.8,4.5,4.6,5.6,6.5,12.6,14.5,34.9,39.85881210.9,13.2,23.0,74.7,78.7,96.0,114.7,120.0,129.6,145.3,269.0,899.75301178.7,98.3,106.6,134.8,182.6,193.7,293.0,306.4,604.5,2911.8,6216.347116185.1,228.9,350.7,538.7,734.2,807.0,1221.2,1239.9,2210.8,5553.0,8823.5,11492.0,12385.9,13531.0,16462.0,26550.0

根据表1中的试验数据(第一列与第三列)，利用最小二乘法，对式(7)中的未知参数进行估计，得m=17.999 9，C=9.675 2×1054。则单向碳/环氧复合材料试样的s-N曲线的方程式为：

s17.999 9N=9.675 2×1054

(14)

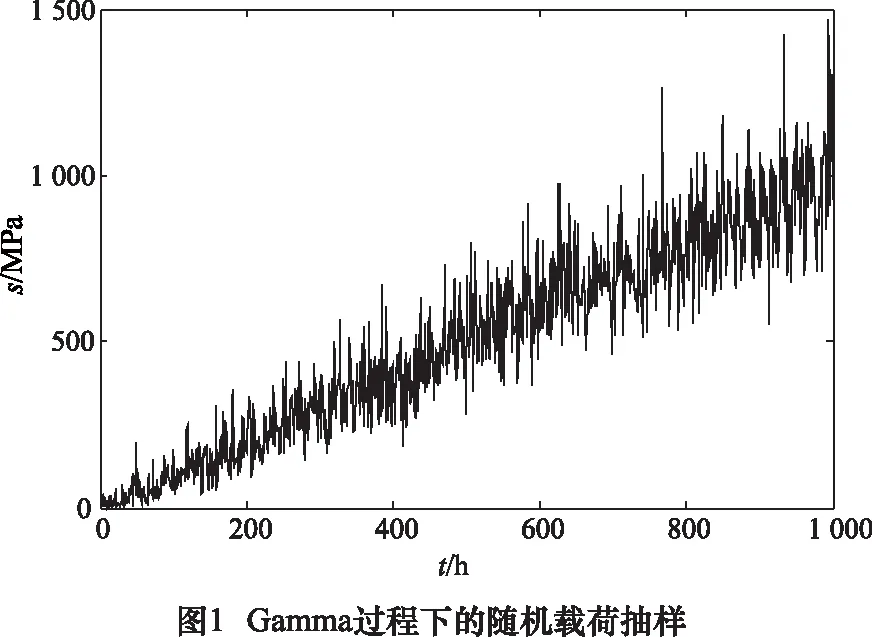
零件在随机载荷作用下工作，载荷加载过程用平稳的Gamma过程描述，a=0.05，b=20。对随机载荷进行抽样分析，仿真结果如图1所示。对零件的可靠度进行Monte Carlo仿真，运用式(13)可得零件的可靠度变化曲线如图2所示。由图2可知，零件的可靠度曲线随着时间的增加具有明显下降的趋势，在t=630 h之前，零件能保持稳定工作，之后零件的可靠度迅速降低，并最终不能满足工作需求而发生失效。

5 结语

本文利用Gamma过程来描述随机载荷作用，基于经典的Miner累积损伤理论，推导了随着载荷作用而产生的强度不断降低的强度退化模型。结合传统的应力-强度干涉模型，提出了一种基于随机过程的应力-强度单向相关下的零件动态可靠度分析方法，并建立了相应的可靠度模型。通过算例验证了模型的有效性。算例结果表明：该模型能够有效用于可靠性分析，具有一定的工程指导意义。

[1]张义民. 机械动态与渐变可靠性理论与技术评述[J]. 机械工程学报, 2013, 49(20): 101-108.

[2]王正, 康锐, 谢里阳. 随机载荷多次作用下的零件失效率计算模型[J]. 北京航空航天大学学报, 2009, 35(4): 407-410.

[3]王正, 谢里阳. 不确定性载荷作用下的零件时变可靠性模型[J]. 航空学报, 2009, 30(7): 1243-1247.

[4]左勇志, 刘西拉. 结构动态可靠性的全随机过程模型[J]. 清华大学学报, 2004, 44(3): 395-397.

[5]孙权, 赵建印, 周经纶. 复合应力作用下强度退化的应力-强度干涉模型可靠性统计分析[J]. 计算力学学报, 2007, 24(3): 358-361.

[6]方永锋, 陈建军, 马洪波. 共同随机载荷下结构动态可靠性分析[J]. 应用力学学报, 2016(2): 345-351.

[7]方永锋, 陈建军, 马洪波. 多种随机载荷下的结构动态可靠性计算[J]. 振动与冲击, 2013, 32(1): 118-121.

[8]王新刚, 张义民, 王宝艳. 机械零部件的动态可靠性灵敏度分析[J]. 机械工程学报, 2010, 46(10): 188-193.

[9]高鹏, 谢里阳. 基于相关性分析的载荷-强度干涉模型[J]. 东北大学学报, 2010, 31(12): 1753-1756.

[10]Schaff J R, Davidson B D. Life prediction methodology for composite structures[J]. Journal of Composite Materials, 1997, 31(2): 128-157.

[11]谢里阳, 王正, 周金宇，等. 机械可靠性基本理论与方法[M]. 北京: 科学出版社, 2009: 77-79.

[12]杨智, 王术新, 董华玉, 等. 载荷-强度相关的机械零件动态可靠性分析[J]. 装甲兵工程学院学报, 2014, 28(2): 17-19.

[13]徐人平, 詹肇麟, 段小建. 复合材料疲劳寿命数据研究[J]. 材料开发与应用, 1994, 9(4): 18-21.