全桥MMC柔性直流输电系统冗余度优化方法

荣 飞， 李文君， 饶 宏， 周保荣， 黄守道， 田新华(. 湖南大学电气与信息工程学院, 湖南 长沙 4008； . 直流输电技术国家重点实验室， 南方电网科学研究院有限责任公司， 广东 广州 5060)

1 引言

基于模块化多电平(Modular Multilevel Converter，MMC)换流阀的柔性直流输电是构建智能电网的重要装备，是改变大电网发展格局的战略选择[1-3]。MMC换流阀的经济性能和供电可靠性对柔性直流输电技术的发展起着至关重要的作用[4-6]。MMC换流阀中功率器件的损耗及其热应力制约着供电系统的供电可靠性，增大MMC换流阀的冗余度时，保证了供电可靠性的增大，但同时也会带来更多的损耗。因此，换流阀损耗与供电可靠性相互影响，相互制约，成为柔性直流输电系统亟待解决的难题[7]。

目前已有很多文献对MMC换流阀的损耗和供电可靠性进行了分析。文献[8]提出了一种MMC换流阀的全桥损耗优化策略，提高了功率传输能力；文献[9]分析了MMC换流阀工作过程中产生的损耗，提出了不同的方法对损耗进行准确的计算；文献[10]根据MMC换流阀的工作机理分析了不同部分的阀损耗，基于实际的电压、电流波形，采用分段解析的方法计算MMC换流阀的阀损耗；文献[11]分析了MMC换流阀及其子模块的可靠性，综合考虑工程实际因素，提出了MMC子模块冗余配置的计算方法；文献[12]构建了两种备用策略下MMC换流阀的可靠度函数并对其进行分析；文献[13]综合考虑了供电可靠性、冗余子模块利用率和冗余子模块数量，提出了一种冗余子模块优化配置方法。

文献[8-13]都没有综合考虑MMC换流阀冗余度对阀损耗的影响。在MMC实际运行中，冗余子模块数增加，可以使系统供电可靠性增强，但必然会造成更大的器件损耗。因此，本文同时考虑柔性直流输电系统的供电可靠性和阀损耗，采用遗传算法得到最优冗余度，本文研究对MMC换流阀设计具有重要参考作用。

2 MMC阀损耗的分析与计算

2.1 MMC换流阀的阀损耗构成

图1为MMC换流阀拓扑结构及其子模块拓扑结构图。MMC换流阀包括A、B、C三相，每相由上下桥臂构成，每个桥臂由N+N0(N0为冗余模块数，N为额定模块数)个相同的子模块(Sub-Module，SM)和一个桥臂电感L级联而成。MMC换流器的子模块由4个IGBT和4个反向续流二极管构成的全桥与储能电容并联而成。此时，通过改变子模块的投入个数，可以灵活改变输出功率及电压等级。

图1 MMC拓扑结构及其子模块结构Fig.1 Topology diagram of MMC and structure of its submodule

根据MMC换流阀的工作原理，可得MMC的阀损耗分类，如图2所示。其中，IGBT的截止损耗、驱动损耗和二极管的截止损耗、开通损耗的值很小，在计算子模块损耗时可忽略不计[7]。因此，MMC换流阀的阀损耗为：

Ptotal=6(PTcon+PTsw+PDcon+Prec)

(1)

图2 换流阀损耗分类图Fig.2 Legend of converter losses

2.2 MMC换流阀各器件通态损耗

柔性直流输电系统中，MMC换流阀的子模块数一般较多。因此，本文采用最近电平逼近(NLM)的调制方法进行分析。为了便于分析，定义冗余度δ为：

(2)

式中，N0为冗余模块数；N为额定模块数。以A相上桥臂为例进行分析，t时刻处于投入状态的子模块个数nap为：

nap(t)=round[N(1-msinωt)/2]

(3)

将式(3)离散化后得：

nap(kT)=round[N(1-msinkωT)/2]

(4)

式中，T为控制周期；t表示时间；m为电压调制比；k表示第k个控制周期；round()为取整函数。

根据器件厂商提供的数据手册，采用线性插值的方法可以得到IGBT的通态电压偏置UCE0和通态电阻rce，二极管的通态电压偏置Uf0和通态电阻rf。精度要求不高时，IGBT的通态损耗PTcon和二极管的通态损耗PDcon可表示为：

(5)

式中，ice和if分别为IGBT和二极管导通时流经的电流，实际工作过程中，ice和if都等于流经A相上桥臂的电流iap。

对式(5)进一步变形可得：

(6)

本文采用全桥MMC换流阀结构。根据全桥MMC换流阀的工作原理可知，当A相上桥臂电流iap为正时，二极管D4始终导通，电流流经nap个二极管(D1)和N-nap个IGBT(T2)，且二极管D4始终有电流流过；当A相电流iap为负时，电流流经nap个IGBT(T1)和N-nap个二极管(D2)，且T4始终有电流流过。此外，冗余子模块也会产生损耗，当A相上桥臂电流iap为正时，T2、D4始终有电流流过；当A相上桥臂电流iap为负时，T4、D4始终有电流流过。因此，电流的正负不同，MMC换流阀产生通态损耗器件的类型及其对应个数也不同。

本文依据桥臂电流的正负将通态损耗进行分段计算。如图3所示，除冗余子模块外的任一子模块的工作状态规律如下：

图3 桥臂电流与触发信号的关系Fig.3 Relationship between arm current and trigger signal

(1)t1～t2，D1、D4导通，子模块处于投入状态。

(2)t2～t3，T2、D4导通，子模块处于切除状态。

(3)t3～t4，D2、T4导通，子模块处于切除状态。

(4)t4～t5，T1、T4导通，子模块处于投入状态。

冗余子模块的工作状态规律如下：

(1)t1～t3，T2、D4导通。

(2)t3～t5，T4、D4导通。

最终得到A相上桥臂的通态损耗Pcon，Pcon由两部分组成：N个子模块的通态损耗Pcon1和N0个冗余子模块的通态损耗Pcon2，其表达式为：

Pcon=Pcon1+Pcon2

(9)

式中

(10)

T0为工频周期；ω为交流电压的基波角频率；φ为MMC换流阀额定功率因数角。

2.3 MMC各器件开关损耗

根据各器件的工作机理，MMC各器件的开关损耗Psw包括参考电压引起的必要开关损耗Psw1、均压控制引起的附加开关损耗Psw2以及冗余子模块的开关损耗Psw3。

根据子模块的开关损耗曲线，采用二次线性拟合得到MMC换流阀的各器件开关损耗表达式为：

(11)

式中，a1,2,3、b1,2,3、c1,2,3为拟合系数；PTon为IGBT的开通损耗；PToff为IGBT的关断损耗；PDrec为二极管的反向恢复损耗；iD(t)、iT(t)分别为流过二极管、IGBT的电流。

在kT时刻，需要发生动作的子模块数为：

nsw(kT)=|nap(kT)-nap((k-1)T)|

(12)

假设MMC换流阀交流侧电流滞后于电压，如图4所示，则：

(1)0～t11，D1关断，T2导通，D4始终导通。

(2)t11～t21，T1关断，D2导通，T4始终导通。

(3)t21～t31，D2关断，T1导通，T4始终导通。

(4)t31～t41，T2关断，D1导通，D4始终导通。

图4 换流阀上桥臂电压与上桥臂电流示意图Fig.4 Comparison of upper arm voltage and upper arm current of converter

由上述分析可知，A相上桥臂在一个工频周期的必要开关损耗Psw1为：

(13)

式中

(14)

为降低开关频率，减小损耗，延长器件使用寿命，本文在典型均压控制的基础上加以改进。改进后的均压控制中增加一个控制率η，即在第k个控制周期内，将已经投入运行的ηnsw(kT)个子模块切除，投入等量未投入的子模块，实现均压控制。根据上述分析可知，当η一定时，均压引起的附加开关损耗仅与控制周期有关，其计算公式为：

(15)

一个工频周期内，t11时刻冗余子模块的T2、D4关断，T4、D2导通，冗余子模块的开关损耗Psw3为：

(16)

A相上桥臂的总开关损耗Psw为：

Psw=Psw1+Psw2+Psw3

(17)

因此，MMC换流阀的总损耗为：

Ptotal=6(Pcon+Psw)

(18)

定义MMC换流阀的损耗率为：

(19)

式中，S为额定容量。

3 MMC换流阀的可靠性分析与计算

MMC换流阀在一定的时间内不出现故障并停止运行的概率称作MMC换流阀的可靠性RMMC。分析MMC换流阀的拓扑结构图可知，子模块SM的可靠性RSM决定MMC换流阀的可靠性RMMC。

每个桥臂上包含N0个冗余子模块，若正常工作的子模块发生故障，则冗余子模块会替代故障子模块投入运行；若发生故障的子模块个数大于N0，系统则停止运行。

则，MMC换流阀的可靠性RMMC为：

(20)

4 冗余度的优化

由第2、3节的分析可知，子模块个数N一定时，冗余度越大，可靠性越高，但MMC换流阀的阀损耗就越大。为了选取合适的冗余度使MMC换流阀处于最优运行状态，本文采用了线性加权和法进行多目标优化，定义目标函数为：

F(δ)=w1L(δ)-w2RMMC(δ)

(21)

由工程经验可知，柔性直流输电系统中基于全桥型MMC换流阀的损耗一般不会超过总容量的2%；工程实际中，MMC换流阀的可靠性为0.998～0.9999。由此，得到综合目标函数的约束条件：

(22)

式中，w1、w2分别为损耗率、可靠性的权系数，取值为：

(23)

其中，D为冗余度δ的取值范围，可以根据式(19)、式(20)、式(22)进行反算得到。

采用遗传算法求最优的冗余度，具体步骤如下：

(1)基因编码：每一条基因采用7位的二进制数进行编码，表示一个冗余度，此时满足精度0.001。

(2)初始种群的生成：群体规模的大小取为50。选择50个冗余度数值作为初试种群，即随机生成50组7位二进制数作为遗传的第一代。

(3)选择：首先计算出每个冗余度值对应的目标函数值，选取40个最小的目标函数值对应的二进制数遗传到下一代，并将最大目标函数值对应的二进制数复制10个补充到下一代群体中。

(4)交叉：对步骤(3)生成的群体进行随机配对，随机设置交叉点，并以一定的概率在交叉点进行0、1置换。交叉后的二进制数替代原来的二进制数进入下一代繁殖。

(5)变异：从步骤(4)产生的50组二进制数中，随机选择10组二进制数，对其以一定概率进行变异。即随机选择该10组二进制数的变异位置进行0、1翻转。

(6)中止：当连续5次遗传后，前后两代的最低目标函数值相差都小于0.001时，则进化完成。此时最小目标函数值对应的二进制数是最优个体，即为最优冗余度。否则转入步骤(3)。

最后，将二进制数表示的冗余度转化为十进制数即可得到MMC换流阀的阀损耗和可靠性都较好的最优冗余度。

5 实例验证

为了验证本文提出的柔性直流输电系统中MMC换流阀的冗余度优化方案，本文针对某直流输电系统进行了实例分析。实际工程中，该直流输电系统的直流额定高电压为±800kV，某侧送端为8000MW，采用柔性直流输电技术，子模块个数为100，冗余度为10%，总损耗率为1.17%。本文取直流母线电压Udc为±800kV，额定容量S为5000MW，调制比m为0.9，子模块电容C为20mF,子模块电容平均电压UC为3kV，子模块可靠性RSM为0.98， IGBT器件采用Infineon-FZ1200R45HL3，线性插值得到IGBT的通态电压偏置UCE0为1.342V，通态电阻rce为0.00126Ω，二极管的通态电压偏置Uf0为1.079V，通态电阻rf为0.001109Ω。曲线拟合得到的器件参数如表1所示。MMC换流阀损耗、可靠性与冗余度的关系如图5所示。

表1 器件参数Tab.1 Parameters of device

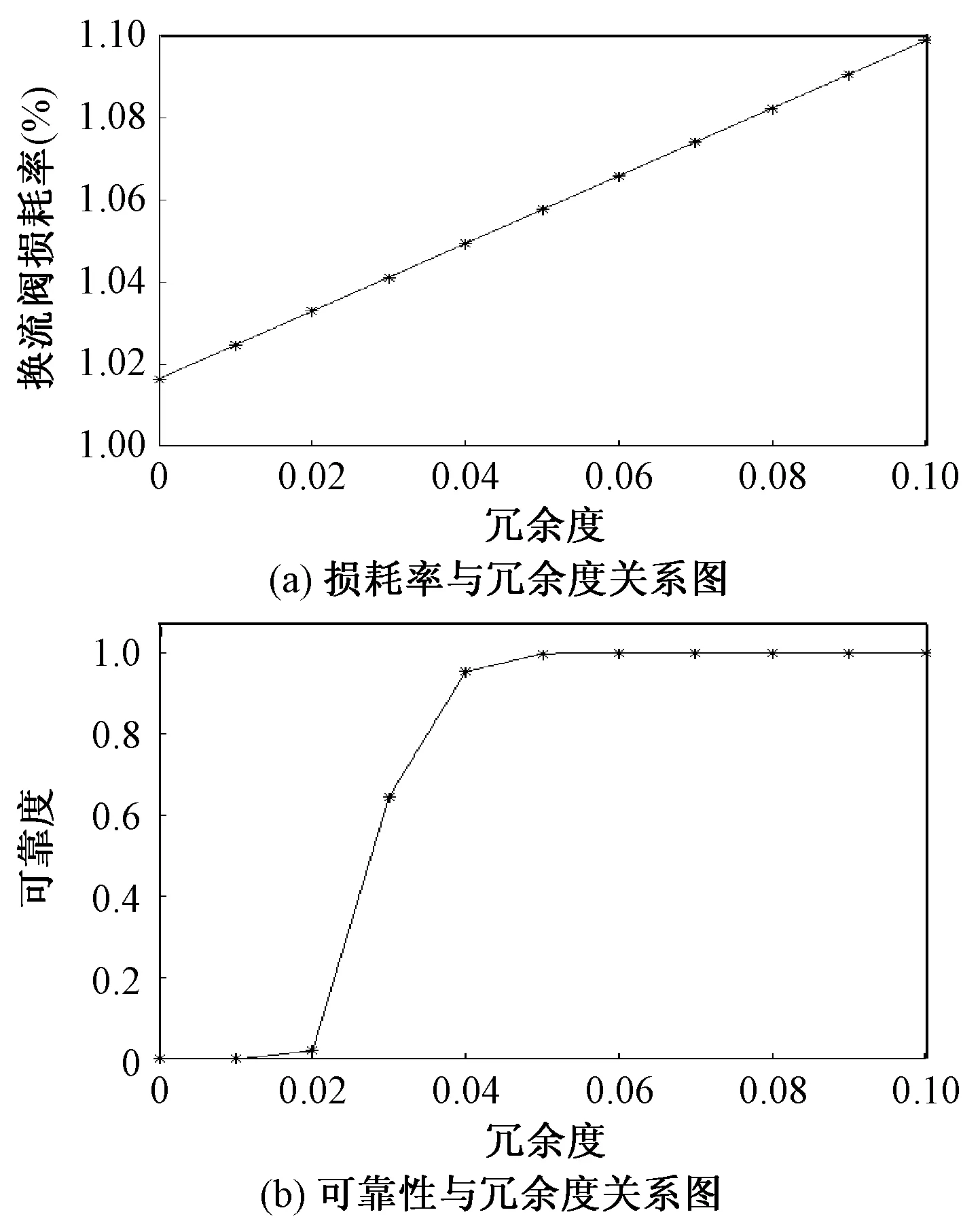
图5 损耗、可靠性与冗余度的关系图Fig.5 Relationship of loss, reliability and redundancy

图5(a)为MMC换流阀损耗率与冗余度的关系，可以看出，随着冗余度的增大，损耗率也相应增大。图5(b)为MMC换流阀可靠性与冗余度的关系，可以看出，当冗余度较低的时候，可靠性也较低；随着冗余度的增大，可靠性迅速增大，但当冗余度大于0.04后，系统的可靠性变化幅度不大。

采用遗传算法对冗余度进行优化计算，优化结果如图6所示。

图6 优化计算结果图Fig.6 Results of optimized calculation

可以看出，经过约25代进化，算法开始收敛，此时对应的冗余度为0.055，MMC换流阀损耗率为1.0616%，供电可靠性为0.9996。相比于工程实际中没有优化的情况，优化后的MMC换流阀损耗更小，冗余度更小，提高了供电效率，减少了子模块的投入。本文研究对MMC换流阀的设计具有重要参考价值。

6 结论

为了提高MMC换流阀的可靠性，一般要设置一定的冗余度。随着冗余度的增大，MMC换流阀的阀损耗增大。冗余度为0～0.02时，对MMC可靠性影响较小；冗余度为0.02～0.04时，可靠性随冗余度的增大明显变大；冗余度大于0.04时，可靠性开始趋于饱和。在保证MMC阀损耗率和供电可靠性的情况下，本文采用遗传算法得到最优冗余度为0.055左右。

[1] 许彬，王平，李子欣，等(Xu Bin, Wang Ping, Li Zixin, et al.).模块化多电平换流器阀段运行试验方法研究(Research on operational test method for modular multi-level converter valves)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2016，35(7)：24-30.

[2] 朱晋，韦统振，霍群海，等(Zhu Jin, Wei Tongzhen, Huo Qunhai, et al.). 适用于架空线的MMC-HVDC换流站子单元拓扑系列(A series of sub-module topology suitable for overhead lines MMC-HVDC)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2015，34(2):20-24.

[3] 饶宏，李建国，宋强，等(Rao Hong, Li Jianguo, Song Qiang, et al.)．模块化多电平换流器直流输电系统损耗的计算方法及其损耗特性分析(The calculation method and loss characteristics of DC transmission system for modular multilevel converter)[J]．电力自动化设备(Electric Power Automation Equipment)，2014，34(6)：101-106．

[4] 胡益，王晓茹，胡柏伟(Hu Yi, Wang Xiaoru, Hu Bowei).基于CPS-SPWM调制方法的MMC-HVDC输电系统冗余保护策略研究(Redundancy protection strategy research of MMC-HVDC transmission system based on CPS-SPWM modulation method)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2016，35(10):9-16.

[5] 王海田，汤广富，贺之渊，等(Wang Haitian, Tang Guangfu, He Zhiyuan, et al.)．模块化多电平换流器的损耗计算(Calculation of the loss of modular multilevel converter) [J]．电力系统自动化(Automation of Electric Power Systems)，2015，39(2)：112-118．

[6] 董玉斐，杨贺雅，李武华，等(Dong Yufei, Yang Heya, Li Wuhua, et al.)．MMC中全桥子模块损耗分析优化的调制方法研究(An optimal strategy for loss distribution of full-bridge submodules in modular multilevel converters)[J]．中国电机工程学报(Proceedings of the CSEE)，2016，36(7)：1900-1907．

[7] 谢晔源，曹冬明，姜田贵，等(Xie Yeyuan, Cao Dongming, Jiang Tiangui, et al.)．基于模块化多电平换流器的新型全桥损耗优化调制策略(A new full-bridge loss optimization modulation strategy based on modular multilevel converter)[J]．电力系统自动化(Automation of Electric Power Systems)，2016，40(6)：78-84．

[8] 屠卿瑞，徐政(Tu Qingrui, Xu Zheng)．基于结温反馈方法的模块化多电平换流器型高压直流输电阀损耗评估(Evaluation of loss of modular multilevel converter type HVDC based on junction temperature feedback method) [J]．高电压技术(High Voltage Engineering)，2012，38(6)：1506-1512．

[9] 周莹坤，齐磊，蒋舒婷，等(Zhou Yingkun, Qi Lei, Jiang Shuting, et al.)．采用最近电平逼近控制的模块化多电平换流器损耗一致性分析(Modular multilevel converter loss consistency analysis using recent level approximation control)[J]．电网技术(Power System Technology)，2015，39(9)：2490-2497．

[10] 许建中，赵鹏豪，江伟，等(Xu Jianzhong, Zhao Penghao, Jiang Wei, et al.).具备直流故障穿越能力的混合MMC可靠性分析和冗余配置方法(Hybrid MMC reliability analysis and redundant configuration method with DC fault traversing capability)[J].中国电机工程学报(Proceedings of the CSEE)，2016，36(4)：953-959．

[11] 王秀丽，郭静丽，庞辉，等(Wang Xiuli, Guo Jingli, Pang Hui, et al.)．模块化多电平换流器的结构可靠性分析(Structural reliability analysis of modular multi-level converters)[J].中国电机工程学报(Proceedings of the CSEE)，2016，36(7):1908-1914．

[12] 王宝安，谭风雷，商姣(Wang Bao’an, Tan Fenglei, Shang Jiao)．模块化多电平换流器模块冗余优化配置方法(Optimal configuration of modular redundancy for MMC)[J].电力自动化设备(Electric Power Automation Equipment)，2015，35(1)：13-19．

[13] 杨柳(Yang Liu).基于MMC的柔性直流输电控制保护策略及损耗分析(Protection strategy and loss analysis of flexible DC transmission control based on MMC)[D].北京：华北电力大学(Beijing: North China Electric Power University)，2013．