光伏并网逆变器损耗分析及效率优化控制

袁义生， 田纪云,2， 邱志卓(. 华东交通大学电气与自动化工程学院， 江西 南昌 33003;2. 包头铁道职业技术学院机车车辆系， 内蒙古 包头 04060)

1 引言

光伏并网发电技术在德国、日本等发达国家已得到深入研究和推广。近年来，我国光伏并网技术也得到重视，并得到了国家政策和财政支持。但是由于光伏面板效率较低，造成光伏并网发电系统效率偏低，这促使世界各国都对光伏并网逆变器提出了很高的效率要求。

为了提高效率，研制具有高效率的光伏并网系统拓扑结构成为研究热点。文献[1]提出一种交错并联型三电平双降压式全桥光伏并网逆变器，保留了三电平双降压式全桥逆变器转换效率高、开关损耗低等相应的软开关特性。文献[2]深入分析研究了双向反激逆变器应用于光伏并网发电系统的工作原理，与差动控制时存在功率回馈相比较，无功率回馈的单边控制效率更高。

文献[3]提出一种新颖的ZVS软开关并网逆变器拓扑及其控制算法，可同时实现整流和逆变工况的ZVS软开关，但需要额外增加硬件。文献[4,5]利用NPC三电平拓扑来提高光伏并网逆变器效率，另外该拓扑还具有器件耐压低、滤波电感小、开关损耗低和并网电流谐波小等优点。文献[6]提出了一种新颖的单相Boost型SPWM并网逆变器电路拓扑和控制策略，有效解决了储能电感值及其电流大、输出波形过零点附近畸变、变换效率低等固有缺陷，提高了变换效率。

在研究光伏并网逆变器效率优化控制策略方面，文献[7]指出空间电压矢量脉宽调制策略能提高直流电压利用率，进而能够在更低的光伏电压下向电网馈能，提高了整机的运行效率。文献[8]比较分析了应用两种典型SVM调制策略的并网逆变器的损耗，得出SVM5调制策略有利于提高并网逆变器效率。文献[9,10]对双有源桥(DAB)的损耗建模和优化进行一系列研究，建立了较为完善的损耗模型，提出一种可减小开关管所承受电流应力的优化调制算法。文献[11]通过对变压器损耗与匝比关系的分析，提出了优化变压器效率所要考虑的主要因素与一般设计方法，达到整体优化变换器效率的目的，但该方法仅限于具有高频变压器的拓扑。文献[12]研究了基于反激逆变器的准谐振模式微型光伏并网发电系统，利用准谐振模式实现功率管的ZVS开关及电流型并网，提高了系统转换效率，但同样应用范围狭窄。文献[13,14]分析比较了两电平和三电平的器件损耗与频率、功率的关系，指出三电平光伏并网变流器在较大功率、较高开关频率场合有着较好的效率优势。文献[15]提出的欧洲效率优化控制方法可使得各逆变模块根据系统发电功率的变化，优先运行在设定的最高效率点，而且还可以推广至三相光伏并网逆变系统、直流微网中的双向变换子系统等。文献[16]提出一种高效率的拓扑切换型并网逆变器，并给出了在总电流谐波含量约束条件下的以全发电范围内效率最优为目标的在线拓扑切换准则。

文献[1-16]均是针对相应拓扑提出的效率优化策略，应用范围狭窄，故本文提出光伏并网逆变器在线效率优化策略，具体实施方法为：在线改变中间母线电压，搜寻系统最大效率点[17]。该方法可应用于所有具有中间母线电容的两级、准三级、三级式等光伏并网逆变器拓扑中，应用范围广泛，而且易于移植。本文建立了损耗分析模型，计算并绘制了损耗柱状图，设计了最大效率点跟踪 (Maximum Efficiency Point Tracking，MEPT)和最大功率点跟踪(Maximum Power Point Tracking，MPPT)控制算法。最后搭建实验样机，验证理论分析和控制策略的正确性和可行性。

2 拓扑结构

图2 光伏并网逆变器控制框图Fig.2 Control block diagram for grid-connected PV inverter

为了研究具有中间母线电容的这类光伏并网逆变器在线效率优化控制方法，本文选择典型的两级式光伏并网逆变器拓扑，如图1所示。其前级为Boost直流变换器，用来实现电压匹配和电气隔离，后级为全桥逆变器，将前级得到的直流电变换为所需要的交流电。其中Uin为输入电压，由光伏阵列提供；Cin为直流侧原边支撑电容；逆变器输出端直接接市电，并网发电运行；Cb为中间母线电容，实现前后级功率解耦。这种拓扑无高频及工频变压器，效率相对较高。

图1 典型的两级式光伏并网逆变器拓扑Fig.1 Typical two-stage grid-connected PV inverter topology

3 总体控制方案

4 损耗分析

影响逆变器效率的因素有器件选型、驱动电路设计、PCB上导体的寄生参数、控制算法和负载特性等内、外部因素。Ub的控制属于外部因素的关键。

在分析之前先作如下假设：①前后级电路均工作在CCM模式下；②忽略二极管的反向恢复现象；③假设Ub一定范围内变化不改变输入电流iin的平均值Iav_f。

4.1 基本电流公式

因开关器件损耗与其流过的电流有直接的关系，故先推导前级Boost电路中中间母线电压Ub与电感Lf的平均电流Iav_f、电流纹波量Δif、峰值电流ip_f、谷底电流iv_f的关系[17]如下：

(1)

式中，Uin为实际输入电压；Df、Tf分别为开关管Q5的占空比和开关周期。

后级逆变电路采用常用的单极性调制，推导后级逆变电路器件损耗时需考虑开关管占空比Dinv呈正弦量变化，故Ub与电感Linv的纹波电流量Δiinv、峰值电流ip_inv、谷底电流iv_inv的关系[17]如下：

(2)

式中，下标(N)表示第N拍的相应变量；Dinv(N)为后级高频臂开关管第N拍的占空比；Ug为并网电源电压；fo为逆变器输出电压频率；Iav_inv(N)为电感Linv电流第N拍的平均值；Tinv为后级电路开关管的开关周期。

设iv为电感电流的谷点电流，即相应开关管开通时刻的电流；ip为电感电流的峰值电流，即相应开关管关断时刻的电流。

开关管一个周期内的开关损耗[17]可以简化为：

(3)

式中，Kti为电流幅值与电流上升、下降时间的关系系数，两者成正比；Ktv为电压幅值与电压上升、下降时间的关系系数，两者也成正比；uds为开关管关断时所承受的电压。

4.2 前级Boost电路损耗

(1)开关管Q5

假设Q5在电流Iav_f下的导通压降为uon_Q5，根据式(1)中的占空比Df，推导其通态损耗为：

(4)

将式(1)中Q5开关时刻的电流iv_f和ip_f分别替代式(3)中的iv和ip，并标识Q5的电流变化率Kti和电压变化率Kvi分别为Kti_Q5和Kvi_Q5，得到Q5的开关损耗为：

(5)

Q5承受的关断电压uds等于Ub，再将式(1)中iv_f和ip_f代入式(5)，最终得到：

(6)

(2)二极管D

假设二极管D在电流Iav_f下的导通压降为uon_D，根据式(1)中的占空比Df，推导其通态损耗为：

(7)

(3)电感Lf

本文磁心采用Magnetic公司的Koolmμ材料，电感损耗分为铜损Pcu和铁损Pfe。铜损又分为直流损耗和交流损耗，因平均电流不变，直流损耗不变，故仅考虑交流铜损，根据文献[18]中三角波电流峰值与有效值的关系和式(1)中的纹波电流Δif，交流铜损表示为：

(8)

式中，Rac_Lf为前级电感绕组的交流电阻。根据厂家材料特性表铁损为B2ff1.46，其中B为电路工作时电感峰值磁通密度，ff为Boost的开关频率。依据电磁感应公式可推导铁损为：

(9)

式中，NLf和ALf分别为电感Lf的线圈匝数和磁心截面积。

4.3 后级逆变电路损耗

后级全桥逆变器采用了单极性调制，Q3和Q4为工频开关方式，构成低频臂；Q1和Q2为高频PWM开关方式，构成高频臂。由于低频臂开关频率极低，故只需考虑其通态损耗，忽略其开关损耗，假设iinv的有效值不变，所以无需考虑Ub变化对Q3和Q4通态损耗的影响。

以并网输出电压正半周为例，在一个开关周期内，Q1高频工作，Q2的反并二极管D2则续流。器件损耗需依据N值在一个逆变周期内累加得到。

(1)开关管Q1

假设Q1在流过式(2)第N拍电流Iav_inv(N)时的导通压降为uon_Q1(N)，根据式(2)中的占空比Dinv(N)，则Q1的通态损耗为：

(10)

将Q1开关时刻的电流iv_inv(N)和ip_inv(N)分别代入式(3)中的iv和ip，并标识Q1的电流变化率Kti和电压变化率Kvi分别为Kti_Q1和Kvi_Q1，得到Q1第N拍的开关损耗为：

(11)

Q1承受的关断电压uds等于Ub，再将式(2)中iv_inv(N)和ip_inv(N)代入式(11)，最终得到：

(12)

(2)二极管D2

假设二极管D2在电流Iav_inv(N)下的导通压降为uon_D2(N)，根据式(2)中的占空比Dinv(N)，推导其通态损耗为：

(13)

(3)电感Linv

采用与前级电路同款磁心，故其交流铜损和磁损与式(8)、式(9)基本相同，只是在代入纹波电流计算B值时要代入式(2)中相关变量。且因是逆变电路，应逐拍计算。推导第N拍的交流铜损和铁损为：

(14)

式中，B为逆变器工作时电感峰值磁通密度；Rac_Linv为电感绕组的交流电阻；finv为后级逆变器的开关频率；NLinv和ALinv分别为电感Linv的线圈匝数和磁心截面积。

依据式(4)～式(14)归纳得到Ub与各器件损耗的关系，结果见表1(Ub上升时)。

表1 Ub与各器件损耗关系Tab.1 Relationship of Ub and loss of each device

4.4 损耗柱状图

根据4.2节和4.3节的损耗公式，对各器件具体损耗数值进行计算，考察中间母线电压Ub与损耗的关系，进而深入研究Ub对效率的影响。MPP点设置为200V/1000W，改变Ub后计算各器件损耗，得到柱状图，如图3所示。可以看出，Ub越大整体损耗越大。

图3 不同Ub时各器件损耗柱状图Fig.3 Loss histogram of each device under different Ub

温度恒定时，光伏阵列MPP点电压近似不变，输出功率随辐照度的减弱而下降，为方便起见，在上位机中设置相同的MPP点电压值为200V、功率为500～1000W的一系列曲线。分别测试中间母线电压维持在MEP点以及传统固定值(例如360V)下的功率，并计算效率，结果如图4所示。可以看出，母线电压维持在MEP点时得到的效率比母线电压维持在360V时高，说明本文方案可行有效。

图4 Ub为MEP点电压以及Ub=360V工况时效率曲线图Fig.4 Efficiency curve at Ub=MEP and Ub=360V

5 在线效率优化及最大功率点跟踪方法

根据第4节的损耗分析可以初步判断，Ub与光伏逆变器的效率之间存在密切的相关关系，其他拓扑中可能存在另外一种关系，不便也没必要对每种拓扑进行损耗分析，所以本文提出在线效率优化方法，即在线调节Ub搜寻系统最大效率点；由于光伏电池存在最大功率点跟踪问题，所以将MEPT内嵌到MPPT中，即实时采集输入输出功率，计算效率并动态调整Ub。系统稳定工作时，每隔Δtin启动一次MPPT，而以较小的Δtinv对Ub进行一次MEPT。另外，系统存在较复杂的启动阶段，这点后面详细分析。

5.1 MEPT方法设计

因效率η和Ub特性曲线有4种情况，曲线不一定具有导数为零的峰值，所以本文MEPT方法不宜借鉴电导增量法，而适宜借鉴扰动观察法。

首先将Ub设定一个初始值，然后按照时序在此基础上进行扰动，正负扰动ΔUbdown和ΔUbup不同，以便降低在最高效率点附近波动的可能性。另外根据Ub的变化范围，系统设置了其上、下限值。程序流程图如图5所示。

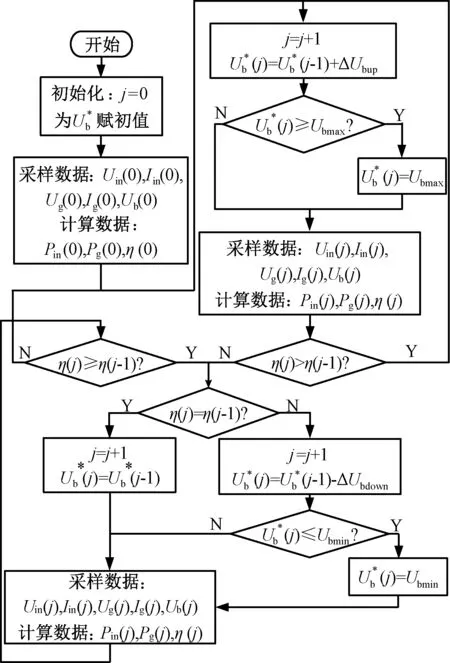
图5 程序流程图Fig.5 Program flow chart

扰动时间间隔Δtinv的选取主要考虑效率计算周期以及Ub扰动后的稳定时间。效率计算周期受后级逆变器的输出功率计算周期影响，后级功率包含直流量和两倍频谐波量，至少一个逆变输出周期才可以计算一次效率。另外需考虑计算精度，采用5个周期计算一次效率均值的方案比较合适。

扰动步长ΔUb的选择与Ub的最大允许调整范围Ubmax～Ubmin，估计的效率变化范围Δη(一般2%以内)，以及DSP的采样和计算精度n(DSP的A/D采样位数减1)有关，扰动步长ΔUb为：

(15)

式中，Ubmax、Ubmin分别为允许的中间母线电压的最大值和最小值。

5.2 MPPT方法设计

为了使系统能够尽快达到最大功率点电压，避免系统在启动过程中对远离最大功率点区域进行搜索造成的功率损耗，采用定电压跟踪法加扰动观察法的复合MPPT方法[19]。

另外，借鉴间歇扫描法的思路，光伏阵列定时地改变阵列电压并工作于该点上，由于实际情况是阵列在一天的运行过程中，短时间内工作点的变化不大，故系统采用每隔500ms启动一次MPPT的方法。这种方法不需要使并网逆变器一直处于搜寻状态，不会产生振荡，同时避免了其他各种方案由于需要实时搜索而引起的功率损失，而且事实证明它对精度的影响几乎为零。

系统存在MEPT和MPPT的配合问题，在稳定阶段，由于两者扰动时间相差较大，所以将MEPT内嵌到MPPT内。与普通扰动观察法不同的是，为了使系统在启动阶段尽快进行MEPT以达到最大效率，本文在系统启动阶段添加一个步长变化计数器，即当每次扰动之后判断扰动步长是否发生变化，每发生一次变化计数器加1。如果步长发生第一次改变，则说明光伏阵列工作点已经越过光伏曲线的顶点；当发生第二次步长的改变时，说明工作点已经完成两次越过光伏曲线顶点，并且下一拍工作点将向着顶点移动，此时阵列必然工作于光伏曲线顶点附近，并在顶点附近振荡。计数器的值等于2，等待一拍，触发启动MEPT。系统启动过程结束之后，设计方法与普通扰动观察法相同。

6 实验结果

实验室制作了一台两级式光伏并网逆变器，中间母线电压初始值为360V。光伏阵列采用PVS1020太阳能电池阵列模拟器代替，利用上位机软件设置一系列P-U曲线，并网端经过继电器直接接市电。其他电路和控制参数见表2。

表2 实验样机参数Tab.2 Parameters of experimental prototype

设置一条开路电压为286V、MPP电压/功率为200V/1000W的P-U曲线。系统启动波形如图6所示。

图6 系统启动波形图Fig.6 System startup waveform

图6中，0～7.7s为系统启动过程，系统首先进行恒定电压法(Constant Voltage Tracking，CVT)，即Ub从开路电压直接降到其80%处，再继续以500ms的时间间隔寻找MPP，并在6.3s附近判断到步长变化计数器等于2，并延时一拍，系统启动MEPT，观察到此时阵列电压在200V附近振荡。Ub初始值设置为360V，第一拍为正向扰动，之后负向扰动，扰动时间间隔为100ms，在7.7s时系统找到最大效率点，最终稳定于最小允许调整值Ubmin处，即325V电压值，之后系统进入稳定工作阶段。另外，图6中Ub启动瞬间存在过冲现象，但很快会稳定在预先设定的360V。系统启动时序图如图7所示。

图7 系统启动时序图Fig.7 System startup sequence

在不同Ub值下测试了三组效率曲线，结果如图8所示。可见无论光伏阵列处于哪个MPP，效率均随Ub的上升而下降；光伏阵列电压相同时，阵列输入功率越高，整机效率越高。

图8 效率曲线Fig.8 Efficiency curves

7 结论

本文首先从效率优化角度出发，提出光伏并网逆变器效率提升的方法，即将整机看做一个黑盒，应用扰动观察法在线搜寻最大效率点对应的中间母线电压。该方法具有应用范围广、不增加硬件开销的优点。

本文设计了光伏并网逆变器的控制方案，提出了前级MPPT和后级MEPT三环控制策略，推导出损耗公式模型，归纳得到中间母线电压与各器件损耗的关系，利用损耗柱状图更加直观地看到每个器件的损耗及总体损耗与中间母线电压的关系。得到在给定范围内，中间母线电压越小，光伏阵列输出功率越大，则整机效率越高的结论。

最后通过实验，验证了本文对光伏并网逆变器的损耗分析和最大效率优化控制策略的正确性与可行性。

[1] 洪峰，万运强，赵鑫，等(Hong Feng，Wan Yunqiang，Zhao Xin，et al．)．一种交错并联型三电平双降压式全桥光伏并网逆变器(A novel interleaved dual-Buck full-bridge three-level photovoltaic grid inverter)[J]．中国电机工程学报(Proceedings of the CSEE)，2014，34(21)：3397-3404．

[2] 毛行奎，王小彬，张锦吉，等(Mao Xingkui，Wang Xiaobin，Zhang Jinji，et al．)．双向反激微功率光伏并网逆变器的分析与设计(Analysis and design for bi-directional Flyback photovoltaic grid-connected micro-inverter)[J]．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2013，32(4)：96-101．

[3] Li R，Ma Z，Xu D．A ZVS grid-connected three-phase inverter[J]．IEEE Transactions on Power Electronics，2012，27(8)：3595-3604．

[4] 马琳(Ma Lin)．无变压器结构光伏并网逆变器拓扑及控制研究(Research on the topologies and control strategies of transformerless grid-connected photovoltaic inverters)[D]．北京：北京交通大学(Beijing：Beijing Jiaotong University)，2009．

[5] 宋金龙(Song Jinlong)．NPC三电平光伏逆变器系统损耗特性研究(Study on the characteristic of system loss of NPC three-level photovoltaic inverter)[D]．合肥：安徽大学(Hefei: Anhui University)，2014．

[6] 陈亦文，江加辉，邱琰辉，等(Chen Yiwen，Jiang Jiahui，Qiu Yanhui，et al．)．单相Boost型SPWM并网逆变器研究(Research on single-phase Boost mode SPWM grid-connected inverter)[J]．电力电子技术(Power Electronics)，2016，46(1)：62-65．

[7] 刘瑶(Liu Yao)．光伏并网变流器损耗分析与优化设计(Loss analysis and optimal design of PV grid-connected converter)[D]．北京：北京交通大学(Beijing：Beijing Jiaotong University)，2011．

[8] 李敏，胡长生，陈敏，等(Li Min，Hu Changsheng，Chen Min，et al．)．基于调制策略的光伏并网逆变器效率优化(Efficiency optimization of grid-connected PV inverter based on modulation scheme)[J]．电源学报(Journal of Power Supply)，2011，9(2)：59-63．

[9] Krismer F，Kolar J W．Accurate power loss model derivation of a high-current dual active bridge converter for an automotive application[J]．IEEE Transactions on Industrial Electronics，2010，57(3)：881-891．

[10] Krismer F，Kolar J W．Efficiency optimized high current dual active bridge converter for automotive applications [J]．IEEE Transactions on Industrial Electronics，2012，59(7)：2745-2760．

[11] 丰瀚麟，肖华锋，谢少军(Feng Hanlin，Xiao Huafeng，Xie Shaojun)．反激型电流源光伏并网逆变器的损耗分析与优化设计(Losses analysis and optimal design of Flyback-type current source grid-connected PV inverter)[J]．太阳能学报(Acta Energiae Solaris Sinica)，2011，32(6)：814-820．

[12] 吴春华，黄建明，杨宇(Wu Chunhua，Huang Jianming，Yang Yu)．高效率微型光伏并网逆变器控制策略研究(Control strategy of high efficiency grid-connected photovoltaic micro-inverter)[J]．电力系统保护与控制(Power System Protection and Control)，2012，40(20)：106-112．

[13] 孙敦虎，刘进军，刘增(Sun Dunhu，Liu JinJun，Liu Zeng)．两级三电平与两级两电平光伏变流器效率分析与比较(Efficiency analysis and comparison between the three-level and two-level PV converter)[J]．电源学报(Journal of Power Supply)，2013，11(1)：20-24, 29．

[14] 李练兵，张雷，孙鹤旭(Li Lianbing，Zhang Lei，Sun Hexu)．三电平光伏逆变器并网控制策略的研究(Research on control strategy of three-level photovoltaic grid-connected inverter)[J]．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2015，34(2)：39-43, 80．

[15] 张犁，胡海兵，冯兰兰，等(Zhang Li，Hu Haibing，Feng Lanlan，et al．)．模块化光伏并网系统欧洲效率优化控制方法(European efficiency improvement control for grid-connected modular photovoltaic generation systems)[J]．中国电机工程学报(Proceedings of the CSEE)，2012，32(9)：7-13, 4．

[16] 孙博(Sun Bo)．拓扑切换型并网逆变器及其在线效率优化技术研究(Research on flexible grid-connected inverter and on-line efficiency optimization)[D]．哈尔滨：哈尔滨工业大学(Harbin: Harbin Institute of Technology)，2013．

[17] 袁义生，田纪云，胡根连，等(Yuan Yisheng，Tian Jiyun，Hu Genlian，et al．)．一种两级式逆变器在线效率优化方法(An on-line efficiency optimization method of two-stage inverters)[J]．电力电子技术(Power Electronics)，2016，46(12)：52-55．

[18] 赵修科(Zhao Xiuke)．开关电源中磁性元器件(Magnetic components in switching power supplies)[M]．南京：南京航空航天大学出版社(Nanjing: Nanjing University of Aeronautics and Astronautics Press)，2004．8．

[19] 李练兵，王同广，孙鹤旭(Li Lianbing，Wang Tongguang，Sun Hexu)．单相光伏并网逆变器的研究(Study on single-phase photovoltaic grid-connected inverter system)[J]．电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2013，32(2)：7-10, 15．