变压器匝数取整对18脉冲变压整流器波形影响的研究

林喜智， 周冀松， 汪邦照， 李善庆， 高静雯， 陈乾宏(. 南京航空航天大学， 江苏 南京 006； . 南京机电液压工程研究中心， 江苏 南京 006；. 合肥华耀电子工业有限公司， 安徽 合肥 0088)

1 引言

多脉冲整流器[1，2]是一种无源整流装置，其利用移相变压器实现网侧电流的多重化，消除低次谐波，实现谐波抑制和功率因数校正(Power Factor Correction，PFC)。相对于有源PFC，其具有可靠性高、过载能力强[3,4]、无附加电磁兼容干扰等优点，广泛用于航空等对可靠性要求很高的场合。多脉冲整流器根据脉冲数的多少，可分为12脉冲、18脉冲及24脉冲变压整流器。其中，18脉冲变压整流器因为变压器结构相对简单、变压器伏安容量较小、网侧波形质量较好等优点，应用更为广泛。

许多文献对多脉冲变压整流器的原理及应用进行了研究。文献[4,5]对18脉冲自耦型变压整流器进行了原理分析；文献[6,7]针对12脉冲自耦型变压整流器开展了优化设计研究；文献[8]则分析了变压器连接方式对12脉冲自耦型变压整流器移相角的影响；文献[9]提出并分析了P型18脉冲隔离型变压整流器的基本原理，实现了输入输出电气隔离和电压变换，并推导了变压器的理想匝比关系。然而，现有文献在分析18脉冲变压整流器工作原理时，多以各线电压矢量相差20°且等长为条件推导匝比关系。但实际变压器必然存在匝数取整，使得变压器实际匝比偏移理想匝比，影响多脉冲整流器的工作特性。文献[10]以12脉冲整流系统为对象，定量分析了绕组匝比变化导致的过移相或欠移相状态对系统的影响。与12脉冲整流器相比，18脉冲整流器变压器参数更多，匝数偏移的分析更加困难。为此，本文以P型18脉冲隔离型变压整流器为研究对象，重点讨论移相变压器匝比偏移对输入电流、输出电压以及网侧相位差的影响，并通过仿真和硬件实验验证了理论分析的正确性。

2 多脉冲原理简述

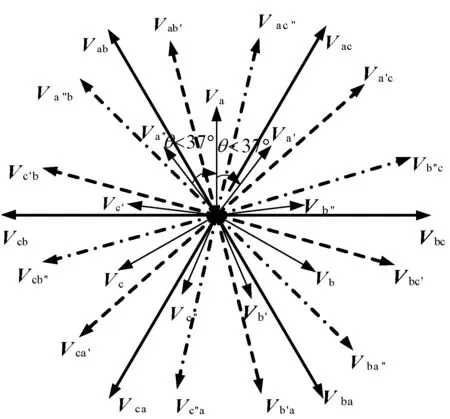
P型18脉冲隔离变压整流器的原理图如图1所示。移相变压器原边为三角形连接，副边为多边形连接。副边输出三组三相电压：一组主桥相电压，两组辅桥相电压，三组电压经三组三相整流桥后并联输出，联接负载。所得输出线电压由两主矢量或一主矢量与一相位差较大的辅矢量构成。为方便描述，将由主矢量之间构成的线电压称为主-主线电压，如Vab；由主矢量和辅矢量构成的线电压称为主-辅线电压，如Vab′，由此绘出输出线电压矢量圆,如图2所示。

图1 P形18脉冲隔离型变压整流器Fig.1 P type 18-pulse isolation transformer rectifier

图2 线电压矢量圆Fig.2 Vector circle of line voltage

根据各节点电流关系，得到方程组如式(1)所示。同时为了防止变压器磁心饱和，需要确保每个磁柱上磁势平衡，磁势平衡方程如式(2)所示。

(1)

(2)

式中，N为原边各绕组匝数；Np1、Np2和Ns分别为副边长绕组和短绕组匝数，且长绕组总匝数满足Np=2Np1+Np2；ia为副边a相电流；ica1为副边aa′绕组电流；isab为原边ab绕组电流；isa为a相输入电流；其他类同。下文变量表述均与此一致。

依据图2线电压矢量圆，文献[9]已给出了匝比关系的具体推导过程，其结果如式(3)所示：

(3)

当式(3)匝比关系成立时，移相角为37°，即两个对应辅矢量如Va′和Va″，与相邻主矢量Va分别滞后和超前37°，则一个周期内输出线电压有18个等幅值波头，且每个波头占20°。18脉冲移相变压器绕制图如图3所示。各磁柱上的绕组满足磁势平衡方程，即绕组电流关系由式(2)确定。

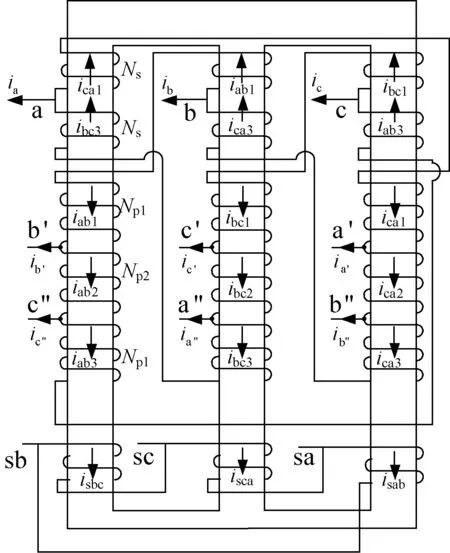
图3 18脉冲移相变压器绕制图Fig.3 Windings of 18-pulse isolation transformer

3 P型18脉冲隔离变压整流器匝比偏移的分析

式(3)给出了副边长短绕组的比例关系，但由此计算出的匝数多为小数，而实际变压器匝数为整数，故实际匝比相对式(3)理想匝比往往有偏差，这将影响整流器的工作性能。因此，本节将讨论匝数取整对输入电流、输出电压和网侧相位差的影响。

3.1 变压器匝数取整对输入电流的影响

首先考虑原边匝数取整。由于原边匝数的变化往往是三相对称变化，取整也是同时向上或向下取，故变压器原边匝数的取整只改变电压幅值变比，而不影响输入电流波形的相位。由式(3)也可知，原边匝数N不在公式中，故不影响移相的情况。因此只需讨论副边实际匝比相对理想匝比的偏差所产生的影响。假设输出负载电流为恒定值Id，原边三相绕组的匝数均为N，联立式(1)、式(2)，化简后可得到isa与匝数关系的一般形式：

(4)

依据图1副边相电压矢量关系，由对称性可知，Vc′+Vb″、Va′+Va″、Vb+Vc、Vb′+Vc″四个合成矢量与Va同相。由于各相电流均与其电压矢量同相，由式(4)可知，最终合成的网侧输入电流均与对应相电压同相[9]。

现由式(4)考虑一般情况。若给定原边匝数N和副边长绕组总数Np，为了直观考察匝比偏差的影响，以式(3)理想匝比为基础，定义实际匝比与理想匝比之比为正系数t1、t2、t3，分别对应Ns、Np1、Np2相对Np的比例关系。同时考虑到匝数关系满足2Np1+Np2=Np，即还需满足以下匝数约束关系：

(5)

由约束关系，可将t3以t2表示，则副边各绕组的实际匝数均可由系数t1、t2和Np表达，即满足：Ns=0.159t1Np，Np1=0.299t2Np，且t1=1、t2=1时为式(3)理想匝比。当上述参量已知，结合式(4)以及图2中线电压输出顺序，即可求得各电流台阶的高度。而为了求出各台阶宽度，亦即一个周期内对应的某一线电压输出的时间，以下根据图1和图2，给出一般情况下的推导过程。

先求取图1中∠c″ab′。原边输入三相电压对称，线电压VAB、VBC、VCA互差120°且大小相等，同一磁柱上电压同相位，绕组电压之比等于绕组匝数之比，则根据回路电压定理可列出方程：

(6)

式中，Vab′为副边ab′端子间的线电压。对式(6)取模，可得大小关系为：

(7)

式中，V为原边线电压VAB、VBC、VCA的有效值。

在变压器副边取Δac″b′，由几何对称性可知Vac″=Vab′。又由余弦定理可得：

(8)

联立式(7)、式(8)并化简，可得∠c″ab′：

cos∠c″ab′=

(9)

由式(9)所得角度，在Δaob′中运用余弦定理，可求得辅矢量大小Vob′：

(10)

为求得移相角θ，在Δaob′中由正弦定理得：

(11)

(12)

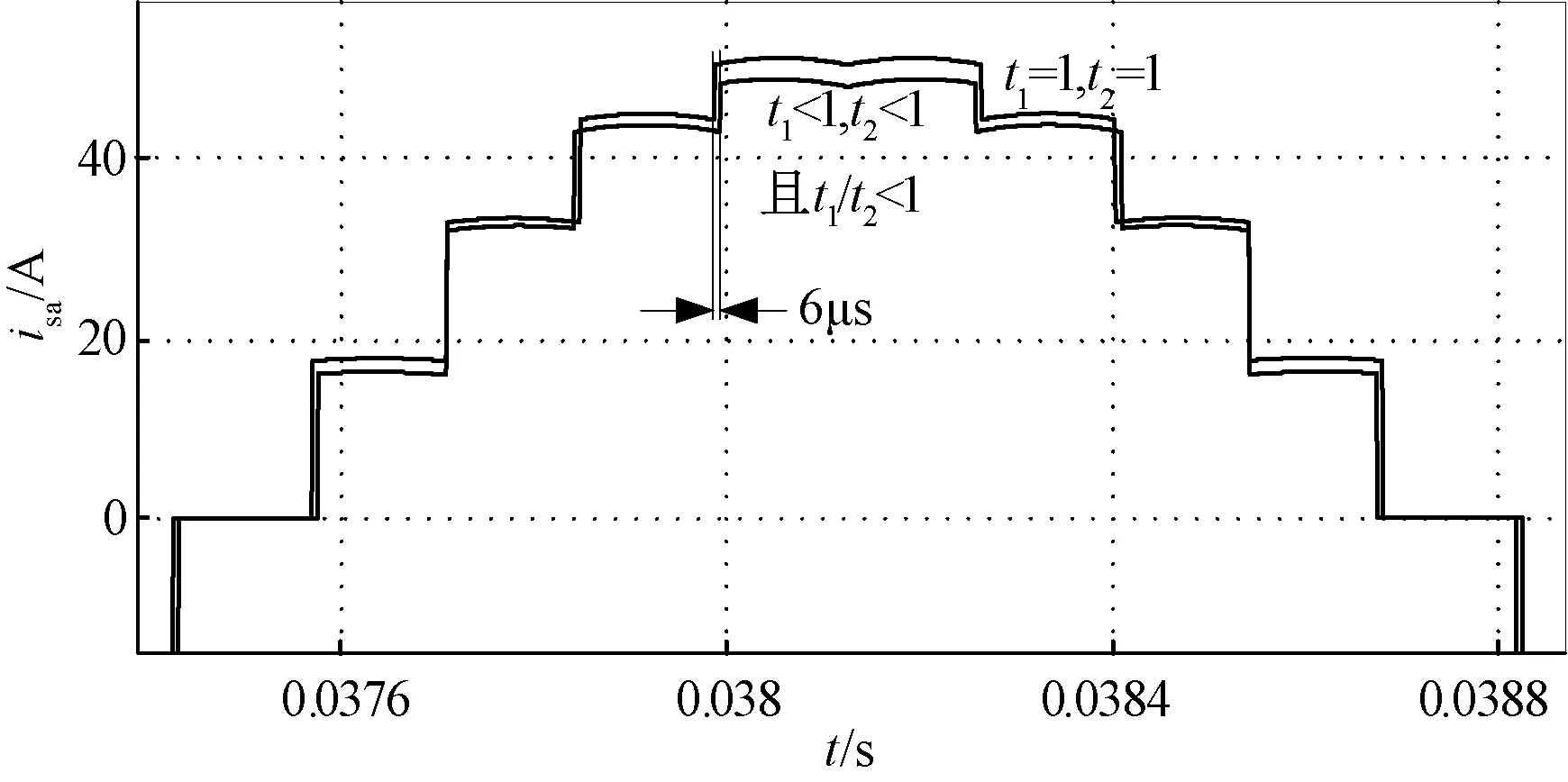
式(12)中F和θ均为已知量，则当0

表1 改变匝比系数时的δ结果 Tab.1 Value of δ when changing turns ratio

理想情况下δ为0，δ为正表示左右延长，δ为负表示左右缩短。由表1可得如下结论：δ关于t1/t2有明显的单调性，δ过零点对应t1=t2=1，此时0.159t1/(0.299t2)=0.159/0.299=0.532。当t1、t2在1附近变化时，只要使实际匝比之比小于该值，即t1/t2<1，则无论t1、t2各自如何变化，总使得主-主线电压输出时间略有延长；若大于该值，即t1/t2>1，总使得主-主线电压输出时间略有缩短；若等于该值，即t1=t2，则无论t1和t2同时增大或同时减小，总使得主-主线电压输出时间不变，即自然换相点相对理想情况无偏移。

实际应用中，为了保证实际匝比尽量接近理想匝比，t1、t2与1的关系可能有多种组合，此处仅就t1<1、t2<1的情况给出分析。t1<1、t2<1即Ns和Np1同时向下取整，此时有两种情况：t1/t2<1和t1/t2>1，这将引起δ改变，影响自然换向角。以t1/t2<1为例，此时主-主线电压占比增加，具体导通角度可由式(12)求得。现假设δ已经求得，对式(4)左右同除以Np，可化为由t1、t2表达的形式。由于三相对称，这里做出A相输入电流波形和A相电压波形，如图4所示。

图4 理想匝比与t1<1、t2<1且t1/t2<1时的A相电流波形及电压波形Fig.4 Current waveforms and voltage waveform of phase A in ideal turns ratio and t1<1，t2<1，and t1/t2<1

以A相输入电流进入正半轴为例，各阶梯对应的副边线电压导通顺序已经标注在图4波形下方。定义从Vc′b依次上升到Vab′的四个电流阶梯分别为阶梯1#～4#，如图4所示，且每个电流台阶高度依次为hi(i=1,…,4)。若纵坐标轴化为图4所示的形式，则各个阶梯高度hi与负载电流Id之比均可求出，且各阶梯hi/Id之差依次为实际匝比。依此规律可以直接根据实际匝比画出各阶电流理论阶梯波。各台阶的系数值hi/Id及其相差关系如表2所示。

表2 各电流台阶对应的hi/Id及hi/Id之差Tab.2 Differences of hi/Id and hi/Id corresponding to each current step

根据表1及表2结果，结合图4，可将输入电流台阶随t1、t2及t1/t2的变化规律总结如下：

(1)只要t1增加，则3#和4#台阶升高，反之不然；

(2)若t1增加，且t2增加，则1#台阶升高，2#台阶需要根据两系数之比确定：若t1/t2<1，则2#台阶降低，若t1/t2>1，则2#台阶升高；

(3)若t1增加，t2减小，则2#台阶升高，1#台阶需要根据实际变化比例确定；

(4)若t1/t2<1，则3#台阶相对理想情况左右各延长δ角度，其余台阶左或右边相应缩减δ角度；若t1/t2>1，则左右各缩减δ角度，其余台阶左或右边相应延长δ角度。

图4给出了理想匝比和t1<1、t2<1且t1/t2<1时的情况，其中负半轴处标记的数值为理想匝比即t1=t2=1对应的情况，与其他文献直接从理想匝比推导出的结果符合。

3.2 变压器匝数取整对输出电压和网侧相位差的影响

由于绕组匝数取整，变压器结构与理想情况有偏差，故图2所示矢量圆将变形，图5为t1<1、t2<1且t1/t2<1匝比偏移时输出线电压矢量圆。由于每个电流台阶均对应一个线电压波头，可由表2通式推知系数对输出电压的影响。当t1<1、t2<1且t1/t2<1时，由于各个电流台阶均下降，故各个线电压矢量相对理想情况均变短。又结合图1几何关系知，Np2比例增加，使得相邻主-辅线电压矢量远离，均向主-主线电压矢量一侧靠拢。考察表2中3#和4#台阶高度通式可知，t1<1时4#台阶下降高度比3#台阶更多，而4#台阶对应主-辅线电压，3#台阶对应主-主线电压，故主-辅线电压矢量相对更短。由图5可见，原本单一矢量圆变为两个同心矢量圆，内部是主-辅线电压矢量圆，外部是主-主线电压矢量圆。两类线电压的峰值偏差以及角度不均匀分布使得输出线电压脉动增加，电能质量下降。

图5 t1<1、t2<1且t1/t2<1时的输出线电压矢量图Fig.5 Vector graph of line voltage when t1<1，t2<1，and t1/t2<1

结合图5还可以给出18个波头消失的条件。由于移相角受t1、t2影响，当t1<1，t2<1，t1/t2<1且t1、t2均进一步减小时，由图5可知主-辅线电压矢量将更加靠近主-主线电压，同时幅值相对主-主线电压更小，当主-主线电压换到主-辅线电压时恰好位于主-辅线电压峰值处，由于主-辅线电压波头已经无法看出，可以认为此时左右对称的主-辅线电压波头消失，只留下主-主线电压波头，进而18波头退化为6波头。仍取副边a相电压为参考相量，则在该临界点处，满足式(13)：

(13)

由于是连续函数，可得：

(14)

因为μ、θ、F均为t1、t2的函数，可由式(14)得到t1、t2关系，即当满足该关系时，可以认为18个波头处于临界消失状态，亦即输出电压能存在18个波头的边界条件。显然，该条件较为极端，需要匝比发生严重偏移，对于匝数取整这类轻微偏移，不会导致波头消失，即一个周期总有18个波头存在。

对比图4两输入电流可见，在t1<1、t2<1且t1/t2<1时，3#台阶即对应Vab或Vac输出，由于该输出是主-主线电压，输出时间较原本20°左右各延长δ，即提前δ输出且延迟δ换相。另三个台阶为主-辅线电压，输出时间相应缩短δ。各台阶相对理想匝比时高度均有下降。虽然相对理想情况而言，各线电压幅值略有偏差，导通时间略有增减，但由于结构上仍然对称，故两辅矢量依旧关于相应主矢量对称，图5矢量圆仍然关于a、b、c相电压矢量所在直线对称，而a、b、c相电压又分别与原边A、B、C相电压同相位，且某相输入电流正负峰值处对称轴原本即与该相电压矢量同相位。可见，输入电流各台阶关于正负峰值处对称轴的左右角度变化和台阶高度变化是等幅度的，峰值对称轴无水平偏移。并且由对称性，阶梯波的对称轴与基波对称轴始终重合，即基波对称轴也无水平偏移。因此只要各相对应绕组匝数按照同一方式取整，就不会导致网侧输入电压与该相输入电流基波产生相位差。

4 仿真及实验结果讨论

为了验证第3节理论分析结果，本文进行了仿真和样机实验。其中仿真参数依据本次实验所用的变压器设置，匝数分别为：原边N=73，副边短绕组Ns=1，副边长绕组Np1=2，Np2=3。依实际匝数修正匝比，并得到对应的系数为：

(15)

首先验证匝数取整对输入电流的影响。按上述实际变压器匝数仿真，可以得到实验所用变压器和理想变压器输入电流波形，图6为A相输入电流正半周波形。需要指明的是，为了突出匝比偏移的影响，仿真电路工作在重载条件，且不考虑各绕组漏感的影响。从图6中可以看出，匝比偏移使得各电流台阶高低宽窄相对理想情况均略有差异。其中，实际匝比相对于理想匝比的输入电流，3#台阶即Vab和Vac对应台阶，由于对应主-主线电压输出，左右均稍有延长，其余主-辅线电压对应台阶均有所缩短，且各台阶均有下降。依据图6仿真结果，可读出换相到主-主线电压的时间相差6μs，则换算得到实验所用变压器相对理想情况的自然换相角之差δ为0.864°。将式(15)匝比关系代入通式，重新求解电角度，得到此时的移相角度θ为34.75°，小于理想时的36.9°。再代入式(12)得到主桥线电压单边延长角δ约为0.8824°，即主-主线电压输出角度左右各延长0.8824°，而主-辅线电压输出时左或右侧将缩短该角度。可见，理论所求的0.8824°与仿真结果0.864°非常接近，证实了理论分析的正确性。

图6 理想和实际匝比下A相电流对比Fig.6 Simulated waveforms of isa with ideal or practical turns ratio

接下来验证匝数取整对输出电压的影响。输出电压仿真波形如图7所示。可见，实际匝数下的输出电压仍然满足一个周期18个波头，但主-主线电压峰值则相对较大，形成了每三个波头中有一个波头较高的波形，使得输出电压的脉动增大，但整体上仍然保持对称。由于t1/t2<1，故主-主线电压输出时间略大于20°，而主-辅线电压导通时间略小于20°，与输入电流对应台阶变化情况相同。

图8为t1=t2<1时输出电压仿真结果对比。其中相对较高的是主-主线电压波头。显然当两系数变化时t1=t2不会出现，这里仅作为进一步理论验证。可见，即使t1和t2的值偏离理想值1，只要两者大小相等，则主-主线电压换相到主-辅线电压的角度是不变的，即各主-主线电压输出时间不变，符合表1中δ的数值计算结果。同时可看出，当t1=t2<1时，两者继续减小，Np2比例增加，使得主-辅线电压峰值向主-主线电压峰值靠拢，而且各电流台阶高度均低于理想情况，故输出线电压波头下降。当t1减小时，由表1可知，4#台阶比3#台阶下降更多，故主-辅线电压相对主-主线电压稍短。仿真结果与图5的矢量圆对应。当主-辅线电压峰值与自然换相点重合时，可以认为处于18波头退化为6波头的临界点，满足式 (13)方程。但实际应用中取整是小范围偏离，t1和t2均在1附近变化，不会导致波头消失。

图8 t1=t2<1时不同取值下输出电压仿真结果Fig.8 Simulated waveforms of output voltage under different values of t1 and t2 when t1=t2<1

最后还仿真验证了匝数取整对网侧相位差的影响。图9为匝数取整时的输入电流与对应相电压的仿真结果。在重载且不考虑漏感时，变压器输入相电压和相应电流基波相位差仍为0。这说明在结构对称时，各相对应绕组以相同方式匝数取整不会导致相位差的产生。以上各仿真结果均符合理论分析。

图9 整匝数下A相输入电压和A相输入电流仿真波形Fig.9 Simulated waveform of input voltage and isa with practical turns ratio

在仿真基础上，本文还对样机进行了硬件测试，得到了相关数据及波形，图10为本次实验所用平台。由于绕组漏感和励磁电感的影响，输入电流台阶无法看出，这里仅给出轻载下不带电容滤波的输出电压交流成分vo(ac)波形，如图11所示。可以明显看见，在一个周期内，共有18个波头，其中每3个波头中就有一个较高波头，即为主-主线电压，略高于主-辅线电压，波形与仿真结果相同。输入相电压有效值为115V时，不同输出功率下测试得到的效率曲线如图12所示。

图10 实验所用平台Fig.10 Test bench

图11 输出电压交流成分Fig.11 AC component of output voltage

图12 变压整流器效率曲线Fig.12 Efficiency curve of transformer rectifier

5 结论

本文以P型18脉冲隔离型变压整流器为对象进行了分析。通过建立一般条件下的数学模型，定量给出了输入电流台阶高度的通式和换相角计算方程，并以两较短绕组向下取整的情况为例进行分析，得到该情况下的相应结论：主-主线电压峰值相对主-辅线电压峰值较高，且输出时间稍有延长；在结构和参数对称且不考虑漏感时，各相对应绕组以相同方式匝数取整不会导致相位差的产生。最后，本文在理论基础上进行了仿真实验，并利用P型18脉冲隔离型变压整流器样机测试验证，仿真和实验结果验证了理论分析的正确性。

附录

(1)辅矢量比例公式为：

(2)移相角大小公式为:

当取t1=t2=1时，θ取得理想值36.9°。

[1] 毛浪 (Mao Lang). 低谐波多脉冲整流器的研究(Research on low harmonics multi-pulse rectifier) [D]．南京：南京航空航天大学(Nanjing: Nanjing University of Aeronautics and Astronautics)，2011．

[2] 崔亮，许爱国，谢少军 (Cui Liang, Xu Aiguo, Xie Shaojun). 高性能航空400Hz变压整流器 (High performance 400Hz transformer-rectifier-unit for aircraft supply) [J]. 电源学报 (Journal of Power Supply)，2012，(6)：71-76, 82.

[3] 任志新(Ren Zhixin). 多脉冲自耦变压整流器(ATRU)的研究(Research on multi-pulse autotransformer rectifier units)[D]．南京：南京航空航天大学(Nanjing: Nanjing University of Aeronautics and Astronautics)，2008．

[4] 毛浪，陈乾宏，蒋磊磊 (Mao Lang，Chen Qianhong，Jiang Leilei). 航空用40kW 18脉冲自耦型变压整流器的研究(The study of 40kW autotransformer based on 18-pulse rectifier for aeronautic application) [J].电力电子技术(Power Electronic)，2011，45(7)：114-116.

[5] Karnath G R, Benson D, Wood R. A novel autotransformer based 18-pulse rectifier circuit [A]. Seventeenth Annual IEEE Applied Power Electronics Conference and Exposition[C]. 2002. 2: 795-801.

[6] 蒋磊磊，陈乾宏，毛浪 (Jiang Leilei, Chen Qianhong, Mao Lang). 12脉冲自耦变压整流器的优化与滤波电感的设计 (Optimization of 12-pulse autotransformer rectifier units and design of filter inductor)[J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2012，31(3)：35-39.

[7] Swamy M M. An electronically isolated 12-pulse autotransformer rectification scheme to improve input power factor and lower harmonic distortion in variable-frequency drives [J]. IEEE Transactions on Industry Applications, 2015, 51(5): 3986-3994.

[8] Meng F, Gao L, Yang S, et al. Effect of phase-shift angle on a Delta-connected autotransformer applied to a 12-pulse rectifier [J]. IEEE Transactions on Industrial Electronics, 2015, 62(8): 4678-4690.

[9] 张鹏真，陈乾宏，毛浪 (Zhang Pengzhen, Chen Qianhong, Mao Lang). 一种18脉冲隔离型变压整流器 (P type 18-pulse isolation transformer rectifier) [J].南京航空航天大学学报 (Journal of Nanjing University of Aeronautics & Astronautics)，2014，46(1)：129-136.

[10] 高蕾，孟凡刚，杨世彦，等 (Gao Lei, Meng Fangang, Yang Shiyan, et al.). 过移相和欠移相对12脉波整流系统的影响及抑制措施 (Influence of over/under phase-shift on 12-pulse rectifier system and its countermeasures) [J]. 电力自动化设备 (Electric Power Automation Equipment)，2015，35(1)：85-93.