变压器油纸绝缘弛豫机构参数小区间计算法研究

陈汉城， 蔡金锭(福州大学电气工程与自动化学院， 福建 福州 350108)

1 引言

时域介电响应法具有简单便捷、无损检测等优势，目前被广泛应用于诊断变压器油纸绝缘老化状态[1]。时域介电响应法包括回复电压法(RVM)和去极化电流法(PDC)两种测试方法，其中回复电压法能较为准确地反映油纸绝缘的缓慢弛豫过程而备受关注[2,3]。现阶段，国内外研究人员深入研究绝缘介质的弛豫响应，并对变压器油纸绝缘等效弛豫机构建模分析。在这些建模分析中，扩展Debye等效弛豫机构模型不仅能准确反映弛豫响应过程，而且能从理论上揭示回复电压特征参数与绝缘响应的深层关系，受到广泛认可。文献[4-6]采用回复电压法从介电响应中提取扩展Debye等效弛豫机构参数作为特征量评估油纸绝缘老化状态，取得较好的效果；文献[7]对扩展Debye等效弛豫机构参数仿真，深入解析油纸绝缘状态变化对扩展Debye模型的影响机理。

扩展Debye等效弛豫机构模型由几何等效机构和弛豫等效机构组成，其中后者可简化为N条Rpi、Cpi参数支路并联形式，但目前研究尚未提出明确的弛豫机构数N的确定手段及各条等效弛豫机构Rpi、Cpi参数的计算方法。文献[8]通过假定变压器油纸绝缘等效弛豫机构数为6条进行电路建模，结果吻合度不高；文献[9]提出利用粒子群、蚁群等智能迭代算法，通过一组非线性方程求解等效机构参数，但其结果未考虑仪器精度等误差分析，且机构数的确定采用经验假定的方法，使得建模结果具有不唯一性；文献[10]应用回复电压法对变压器油纸绝缘拓扑结构辨识来确定机构数N，但并没有提出具体每条弛豫支路参数的计算方法。故有必要提出一种新的弛豫机构建模方法使后续的老化诊断特征量提取更为准确。

鉴于上述不足，本文提出直接应用数学解析法对测试的回复电压曲线分解，并建立弛豫响应方程组，在求解方程组时结合区间数学分析理论，得到最优解即等效弛豫机构的Rpi、Cpi参数小范围区间。最后，通过实例进一步验证了本文提出拓扑机构数分析及参数计算的可行性。该方法解决了等效弛豫机构建模不唯一、机构数确定具有随机性且吻合度不高等问题，使后续的老化诊断特征量数据分析提取具有更高的可靠性及准确性。

2 回复电压测试及扩展Debye建模

回复电压测试技术以时域介电响应作为理论基础，是一种便捷可靠的绝缘诊断方式[11]。回复电压的测试方法如图1所示。首先闭合S1，对变压器绕组施加U0的直流高压，通常为2000V，施加时间设为tc,这段时间绝缘介质进行极化过程；其次，断开S1,闭合S2,对变压器绕组进行短接处理，时间设为td，这段时间绝缘介质进行去极化过程；最后，断开S1及S2，闭合S3，对变压器未释放完全的自由电荷所形成的回复电压进行测量，并记录回复电压参数。同时，在完成数据记录后，再次接通S2，将变压器的残余电荷释放完毕待下一次测量使用。通过回复电压测试方法得到的回复电压曲线如图2所示。

图1 回复电压测量电路图Fig.1 Circuit of return voltage measurement

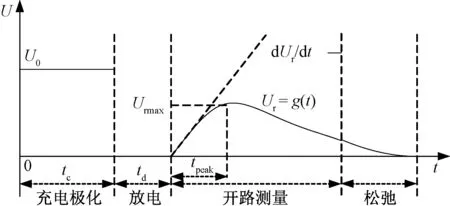
图2 回复电压典型曲线图Fig.2 Return voltage waveform

直接利用回复电压曲线诊断变压器油纸绝缘老化状态的特征量较少，且不能深入分析介质响应弛豫机理。故有必要对变压器油纸绝缘系统进行等效建模分析。现阶段，基于扩展Debye等效弛豫机构建模具有吻合度高、特征量较多等优势[12]，获得广泛认可，如图3所示。

图3 扩展Debye模型图Fig.3 Extended Debye model diagram

3 回复电压函数及特性分析

3.1 回复电压函数

根据第2节的分析，扩展Debye等效弛豫机构能对变压器油纸绝缘系统准确建模，且经研究表明，其与实测回复电压曲线具有较高吻合度。但弛豫机构数N以及各条支路的等效机构参数Rpi、Cpi的计算，若采用假定法和普通粒子群等智能寻优迭代算法，仍具有因弛豫机构数N随意假定带来的建模不唯一、随机性等问题。因此，有必要进一步研究回复电压函数及其特性，寻找新的建模机构参数计算方式。

根据回复电压测试方法，分析1条弛豫支路的极化电容Cpi的剩余电压UCpi单独作用的结果，并假设图3中弛豫等效机构部分所包含的支路数为N，建立剩余电压与回复电压Ur函数关系式[13]，如式(1)所示：

(1)

式中，i=1,2,…,N；MN,i、TN+1、zj,i和pj表示各条弛豫机构响应的弛豫信息函数。

对式(1)进行拉式反变换，可得1条弛豫机构响应的时域关系式：

Uri(t)=(X1,ieq1t+X2,ieq2t+…+XN+1,ieqN+1t)UCpi

(2)

式中，各指数项前面的系数[14]为：

(3)

式中，j，l=1,2,…,N+1；k,i=1,2,…,N。运用叠加定理，考虑所有弛豫机构的残余电压UCpi共同作用，等效弛豫机构回复电压的表达式为：

Ur(t)=G1eq1t+G2eq2t+…+GN+1eqN+1t

(4)

3.2 几何等效机构Cg对回复电压的贡献

为了进一步分离回复电压函数Ur(t)的N+1项弛豫信息，有必要分析几何弛豫机构Cg在回复电压测试后残余电压对回复电压曲线的影响。本文测试多台变压器，得出的结论具有一致性。现选取其中一台变压器T1为例，对变压器T1进行回复电压测试，测试电压为2000V，tc与td的时间比为2∶1，得到回复电压曲线并建立其扩展Debye模型。在扩展Debye模型中，包含Cg弛豫机构与不包含Cg弛豫机构得到的回复电压曲线结果不同，将两次回复电压的计算值相减得到Cg对于回复电压曲线的贡献值，如图4所示。分析可知，扩展Debye模型几何弛豫机构Cg仅对前段时间的回复电压曲线产生影响，而对后段时间的曲线影响几乎为零。

图4 几何等效机构Cg对回复电压的贡献Fig.4 Effect of Cg on recovery voltage

3.3 不同时间常数的弛豫机构对回复电压的贡献

已有研究表明，弛豫等效机构中不同时间常数τ对回复电压函数的贡献值不同。如图5所示，假设函数1和函数2是回复电压函数的两条分支曲线，且函数2的时间常数是函数1的3倍。在t1之后，f1的函数值仅为f2的1%，且随着时间增加，函数f1的数值无限趋近于零，此时回复电压的函数值仅由大时间常数分支曲线f2贡献。

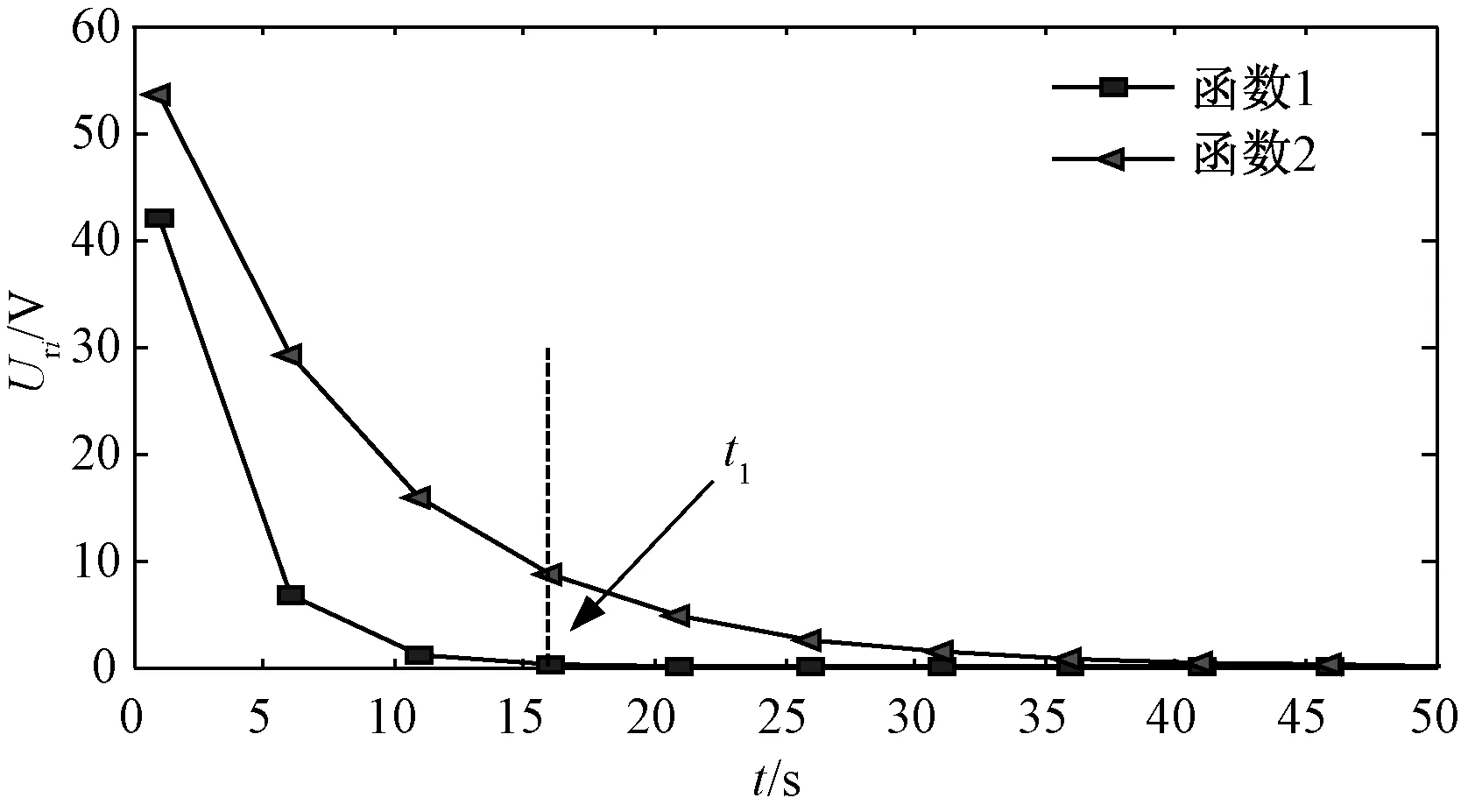
图5 不同时间常数的弛豫机构对回复电压的贡献对比Fig.5 Contribution of relaxation mechanism with different time constants to recovery voltage

由此可见，回复电压函数是N+1个指数函数叠加的共同结果。当回复电压曲线任取靠近曲线末端数据点时，小时间常数分支曲线对大时间常数分支曲线的影响可忽略不计。此时，回复电压曲线可以看成主要由大时间常数分支曲线贡献的结果。

4 弛豫机构参数小范围区间计算方法

4.1 解析弛豫机构数

根据回复电压函数及特性分析，可以应用数学解析法计算变压器油纸绝缘等效弛豫机构参数。具体步骤如下：

(1)利用回复电压测试仪RVM5461现场测试得到待诊断变压器的回复电压数据，并绘制回复电压曲线。

(2)任取回复电压曲线Ur(t)末端两点(t1,Ur(1))和(t2,Ur(2))数据，根据回复电压函数特性分析结果，曲线末端可以看成最大时间常数弛豫机构支路的贡献，由此建立如下方程组：

(5)

由式(5)可以解出G1和q1两个参数，将G1和q1两个参数的结果代入Ur1(t)=G1exp(q1t)，即可求出第1条分支曲线F1。

(3)将回复电压函数Ur(t)减去第1条分支曲线F1，得到剩余曲线H1。再从当前剩余曲线末端同样选取两点数据(t3,Ur(3))和(t4,Ur(4))，根据式(5)，求得G2和q2两个参数并代入Ur2(t)=G2exp(q2t)，得到第2条分支曲线F2。将剩余曲线H1减去第2条分支曲线F1，可得剩余曲线H2。

(4)应用上述方法依次解出第3，4，…，N+1条分支曲线，直到剩余曲线的最大峰值小于预先设定的阈值，得到N+1个弛豫信息。

4.2 应用区间数学分析计算弛豫机构参数

由4.1节分析可知，通过求解分支曲线参数可以得到N+1个弛豫拓扑信息，此时变压器含有N个等效弛豫机构，加上绝缘电阻Rg、几何电容Cg一共有2(N+1)个未知参数待求。为了求出所有的等效模型参数，可对待测变压器进行回复电压测试s次。随着设定的充放电时间tc及td的改变，测试过程中Gi和UCpi不断变化，而qi始终保持不变。故分析可知：

(1)未知量：2(N+1)个等效弛豫机构参数及sN个残余电容电压UCpi。

(2)已知量：s(N+1)个s次测试得到的分支曲线参数Gi及(N+1)个保持不变的qi参数。

当满足2(N+1)+sN≤(s+1)(N+1)时，测试得到的方程组满足参数计算要求。如假设N=4时，s≥5，即至少需要测试回复电压不同充放电时间5次，才能解出变压器油纸绝缘4个弛豫机构的建模参数。由4.1节可知，变压器油纸绝缘弛豫机构数N为已知，故可以建立如下方程组：

为了得到最优解，构造优化目标函数：

(6)

应用粒子群智能优化算法在全局范围内寻优，直到F(X)的值趋近于0。当寻优结果满足精度要求时，即可得到理论上的变压器油纸绝缘等效弛豫机构参数。但在回复电压实际测试中充电电压等测试参数时常会有波动，引起绝缘介质内部电场施加不稳定。经过大量实测验证，充电电压波动时，回复电压曲线具有一定的波动性，其中峰值大小波动最为明显。故本文采用一种新的计算方法，将区间数学分析应用于粒子群算法中，综合利用区间数学的指导性及粒子群算法的全局寻优的优点，提高参数方程计算的准确性。

在粒子群初始化中，粒子群区间的设定速度及位置为：

xi=(xi11,xi12,xi21,xi22，…，xiE1,xiE2)

(7)

式中，E为粒子群的维数。将区间算法融入后，每一维都设定有上下界区间，此时粒子群位置更新公式如式(8)～式(10)所示：

pbestj=pbestj+r,pbestj+1=pbestj+1-r

(10)

为了分析变压器油纸绝缘等效弛豫机构参数小范围区间的可靠性及准确性，本文采用回复电压极化谱吻合度法[15]，如式(11)所示，验证参数计算结果并与采用普通粒子群智能算法结果的准确度作对比分析。

(11)

式中，m为回复电压测试次数；Uri(tp)为第i次回复电压测试的峰值大小；Urimax为第i次回复电压测试建模仿真峰值大小。具体参数计算流程图如图6所示。

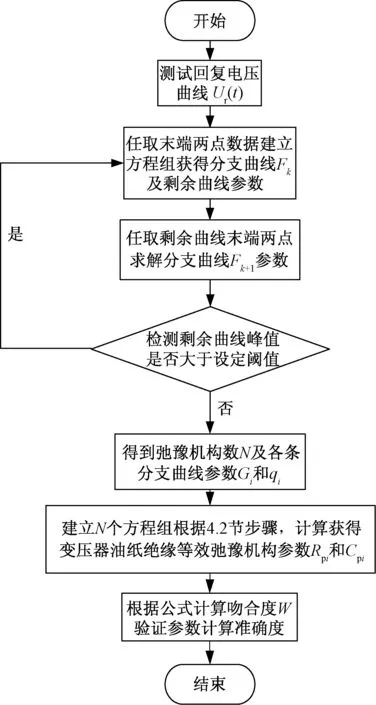
图6 参数计算流程图Fig.6 Parameter calculation flow chart

5 实例验证

本文对42台变压器利用回复电压测试仪RVM5461现场测试得到回复电压数据，如图7所示。回复电压曲线包含弛豫响应信息，应用弛豫机构参数分析计算方法，得到具体的小范围区间，选取小区间中点参数值作为建模的弛豫机构参数，并利用回复电压极化谱吻合度法验证该算法的准确性。因篇幅有限，仅列出10台变压器弛豫机构参数计算结果(弛豫机构参数小范围区间中心值)及吻合度数据以供参考，如表1所示。

图7 回复电压现场测试图Fig.7 Recovery voltage field test

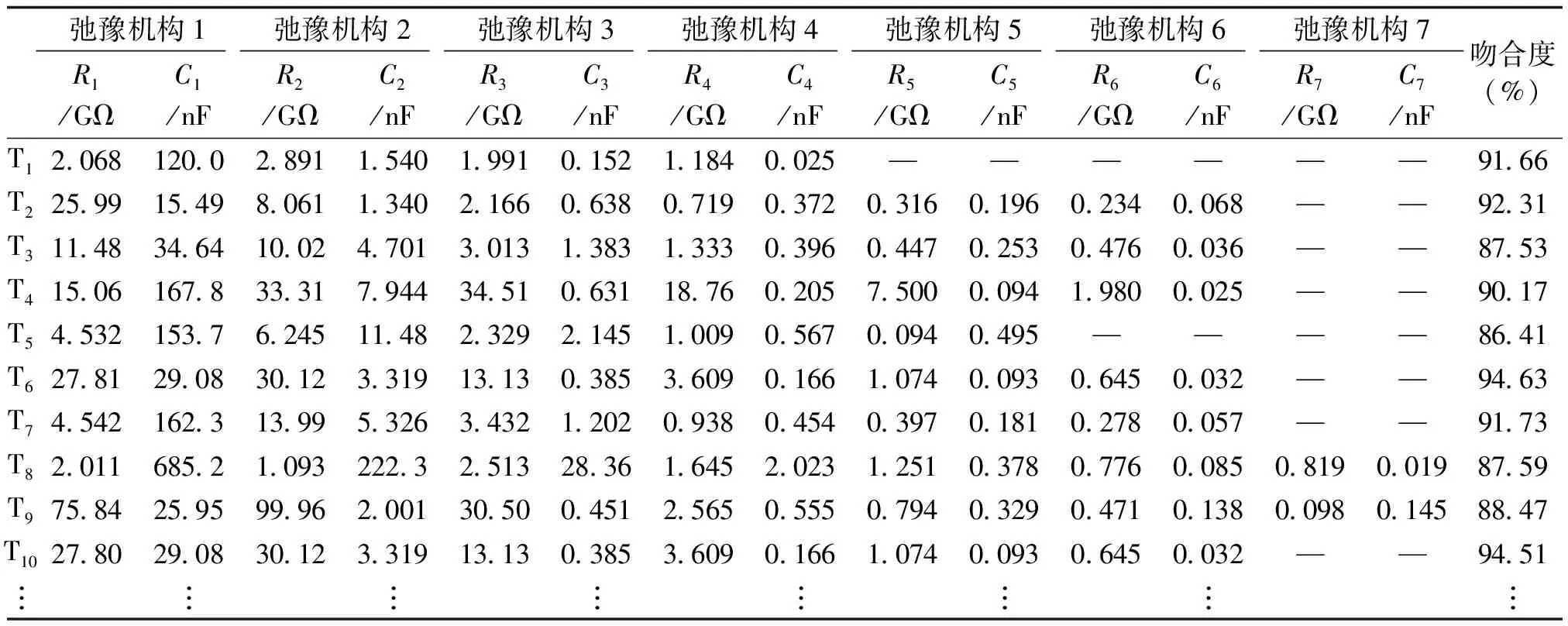
表1 油纸绝缘变压器弛豫机构参数辨识统计表Tab.1 Statistics of relaxation mechanism parameter identification of transformer oil-paper insulation

为了更详细地举例说明本文提出的变压器油纸绝缘弛豫机构参数小区间计算法的具体过程，选取2台不同绝缘老化状态的变压器T1和T2作详细分析计算，此2台变压器的具体信息如表2所示。根据第4节所述步骤，对变压器T1进行回复电压测试，获得回复曲线如图8(a)所示；任取末端两点(t1,Ur(1))和(t2,Ur(2))，根据式(5)建立方程组求解第1条分支曲线参数，同时将原始回复电压曲线扣除第1条分支曲线数据获得剩余曲线，如图8(b)所示；将图8(b)中的剩余曲线末端任取两点(t3,Ur(3))和(t4,Ur(4))代入式(5)中求解第2条分支曲线参数。以此类推，结果如图8(c)～图8(f)所示，直至剩余曲线的峰值小于原始曲线的5%，则停止分解。如图8(f)所示，此时剩余曲线的峰值为1.153V，小于设定阈值，故停止分解并获得5条分支曲线。

表2 变压器T1和T2的基本信息及测试条件Tab.2 Basic information and test condition of transformers

图8 变压器T1分支曲线解析过程Fig.8 Analysis of transformer T1 bifurcation curve

根据上述分析，弛豫等效机构数应为N=4。按照4.2节所述公式及方法，在求得Gi和qi(i=1，2，…，N)的条件下可建立方程组，并应用区间数学分析方法得到最优解，即等效弛豫机构参数小范围区间，如表3所示。将变压器T2按照同样的算法进行参数辨识，由于篇幅有限，不再赘述。具体等效弛豫机构拓扑辨识结果如图9和图10所示。T2的等效弛豫机构数为N=6，区间辨识结果如表3所示。

为了进一步验证应用该方法计算变压器油纸绝缘等效弛豫机构参数的准确度有所提高，将其结果分别与两次应用普通粒子群优化算法的变压器油纸绝缘建模参数辨识结果作对比，并利用极化谱吻合度法，根据式(11)计算得到各自的吻合度，如表4所示。

图9 变压器T2分支曲线解析过程Fig.9 Analysis of transformer T2 bifurcation curve

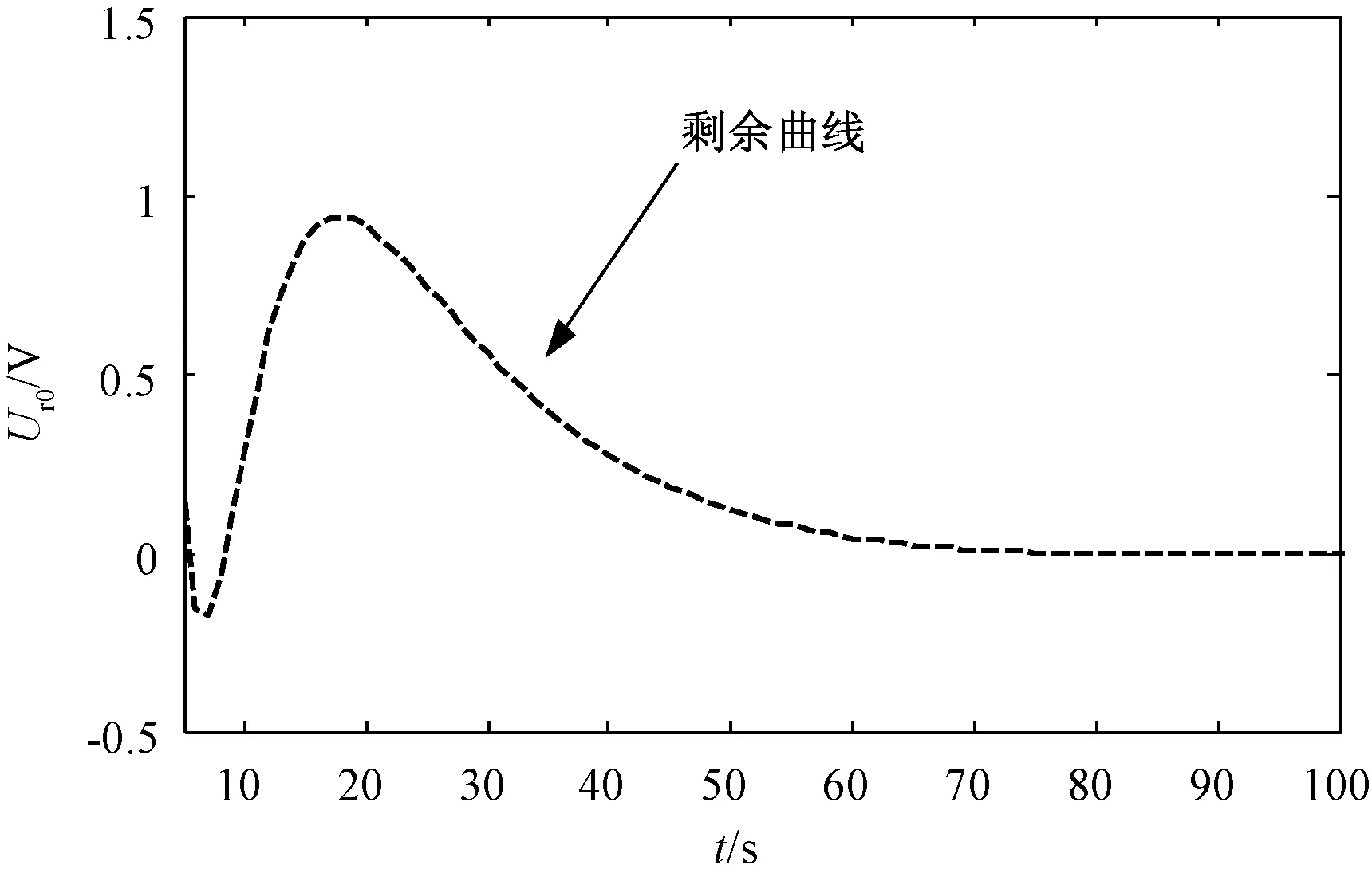
图10 变压器T2解析剩余曲线Fig.10 Residual curve of transformer T2

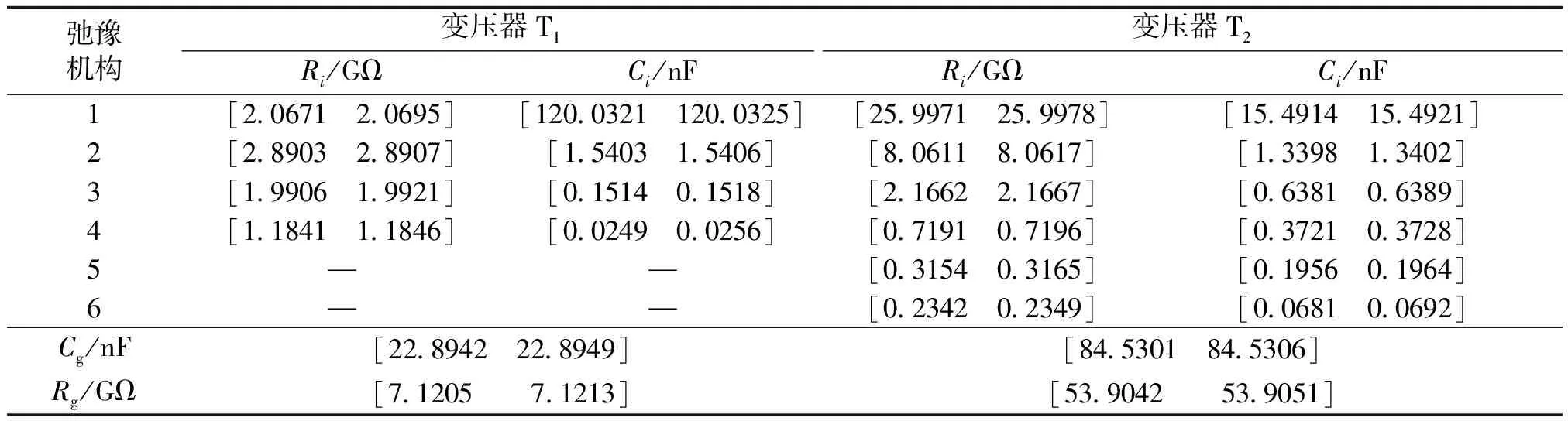
表3 变压器T1和T2参数计算小范围区间Tab.3 Transformer T1 and T2 parameters calculate on small range

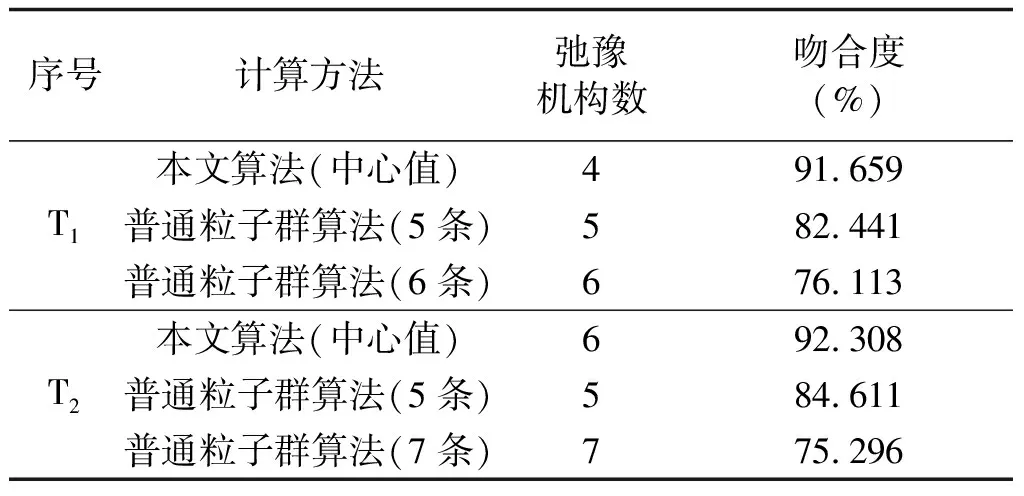
表4 不同算法的极化谱吻合度对比分析Tab.4 Comparative analysis of polarization spectra of different algorithms

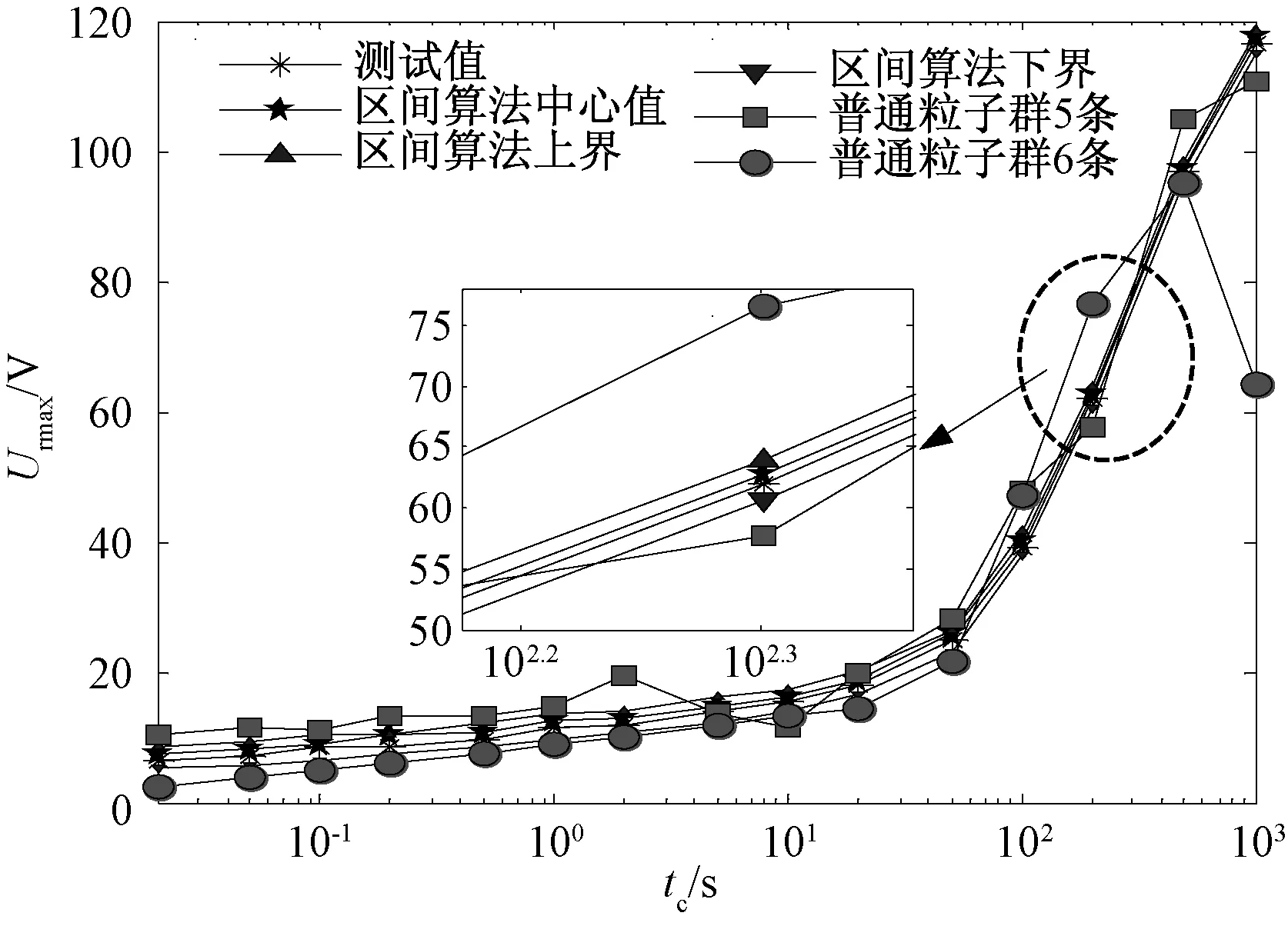
图11 变压器T1极化谱计算值与测试值Fig.11 Calculation value and test value of T1 polarization spectrum

图11和图12分别为变压器T1、T2极化谱计算值与测试值。在实例验证中，两台变压器采用不用的极化支路数的粒子群算法，在各自极化谱线的末端有效大偏差。可以看出，普通粒子群算法在变压器油纸绝缘等效弛豫机构建模中采用任意假定弛豫机构数的方法，其极化谱的吻合度并不高。本文提出的算法通过回复电压函数深入解析弛豫机构数，并考虑仪器精度等不确定因素影响，利用区间数学分析计算变压器油纸绝缘等效弛豫机构小范围参数。本文采用区间算法得到小范围参数的中心值作为建模参数，其吻合度有明显提高。

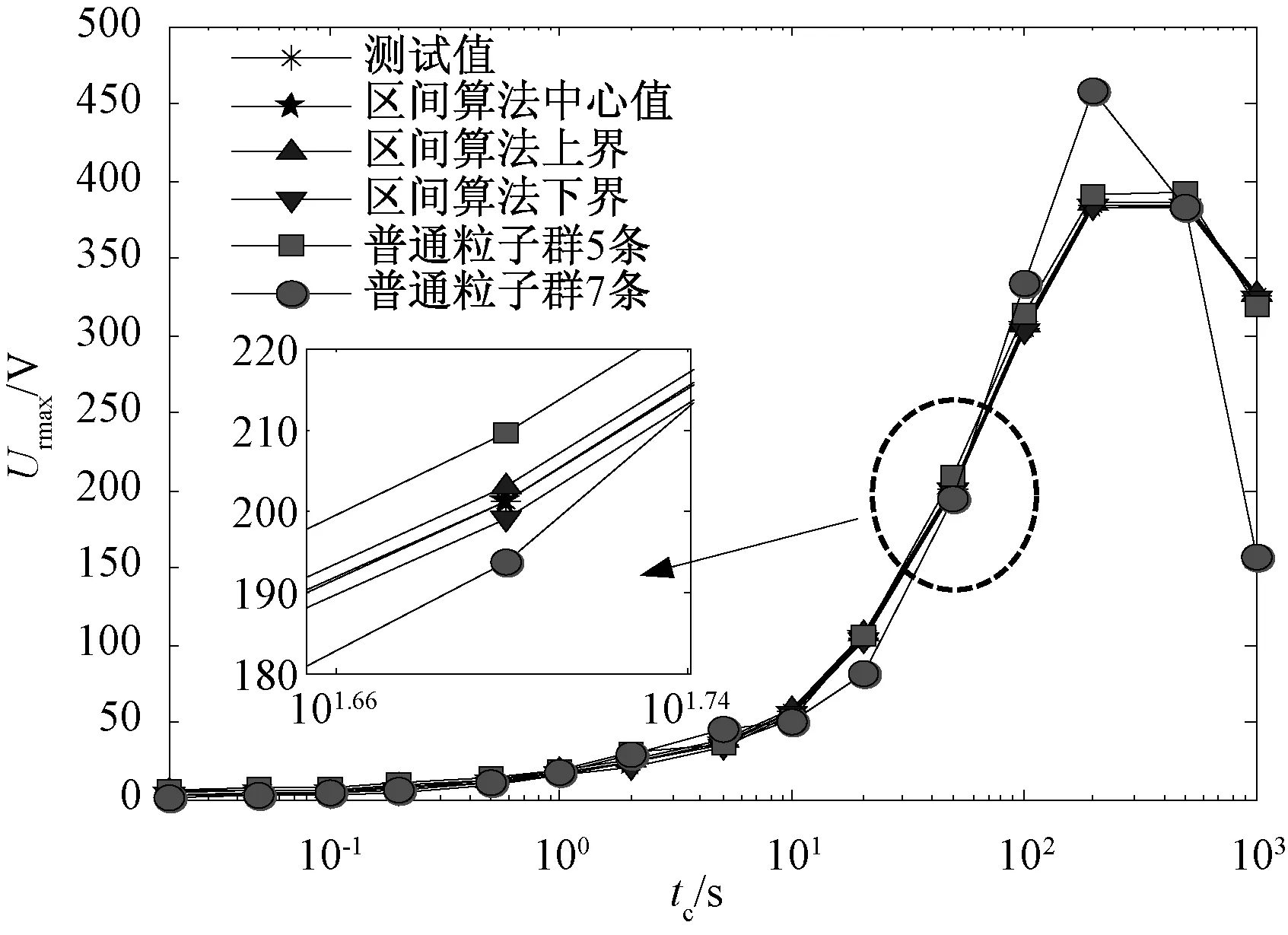
图12 变压器T2极化谱计算值与测试值Fig.12 Calculation value and test value of T2 polarization spectrum

6 结论

现阶段，国内外学者对基于扩展Debye等效弛豫机构建模分析及应用参数计算结果提取特征量诊断变压器油纸绝缘老化状态已有一定程度研究，但在建模过程中的等效弛豫机构数的确定方法及各条分支机构的参数计算中仍存在一些问题，如机构数凭经验任意假定，建模参数计算吻合度不高等。本文提出一种新的变压器油纸绝缘弛豫机构参数辨识方法。

(1)本文提出一种应用回复电压测试曲线深度解析变压器油纸绝缘等效弛豫机构拓扑的新方法。经过多台变压器实测验证，采用解析法分析得到的弛豫机构数建模，其回复电压极化谱对比测试值吻合度较高。

(2)在参数方程计算中考虑因测试误差及仪器精度引起的不确定量。采用区间数学分析方法求解方程组得到最优参数的小范围区间，可以取小范围区间中心值参数建模。

(3)最后，本文通过实测验证该建模方法具有普适性。具体分析两台变压器等效弛豫机构的吻合度，其中变压器T1和T2采用本文提出算法的吻合度分别达91.659%及92.308%，而应用普通粒子群算法在建模过程中具有随机性，吻合度均低于85%。该方法解决了等效弛豫机构建模不唯一、机构数确定具有随机性且吻合度不高等问题，可为变压器油纸绝缘老化诊断特征量数据分析提供可靠的保障。

[1] 赵峰,李硕 (Zhao Feng, Li Shuo). 基于熵权和灰关联度的变压器故障诊断(Fault diagnosis in transformer based on entropy weighted and grey incidence)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2015, 34(1): 57-61.

[2] Saha T K, Purkait P. Understanding the impacts of moisture and thermal ageing on transformer’s insulation by dielectric response and molecular weight measurements[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2008, 15(2): 568-582.

[3] Wolny S. Aging degree evaluation for paper-oil insulation using the recovery voltage method[J]. IEEE Transactions on Dielectrics & Electrical Insulation, 2015, 22(5): 2455-2462.

[4] 刘捷丰，廖瑞金，吕彦冬，等(Liu Jiefeng, Liao Ruijin, Lv Yandong, et al.).电力变压器油纸绝缘含水量定量评估的时域介电特征量(Time domain dielectric characteristics for quantitative assessment of moisture content in transformer oil-paper insulation)[J].电工技术学报(Transactions of China Electrotechnical Society), 2015, 30 (1): 212-219.

[5] Jota P R S, Islam S M, Jota F G. Modeling the polarization spectrum in composite oil/paper insulation systems[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1999, 6(2): 145-151.

[6] Chen D, Yang Y. Attribute reduction for heterogeneous data based on the combination of classical and fuzzy rough set models[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(5): 1325-1334.

[7] 邹阳,蔡金锭(Zou Yang, Cai Jinding).油纸绝缘变压器时域极化谱特性实验分析(Experimental analysis on time-domain polarization spectrum of oil-paper insulation transformer)[J].电工技术学报(Transactions of China Electrotechnical Society),2015,30(12):307-313.

[8] 江修波，黄彦婕，赖祥生(Jiang Xiubo, Huan Yanjie, Lai Xiangsheng).改进蚁群算法及其在变压器绝缘介质响应电路参数计算中的应用(Improved ant colony algorithm and its application in parameter identification for dielectric response equivalent circuit of transformer)[J].高电压技术(High Voltage Engineering),2011,37(8):1982-1987.

[9] 蔡金锭,林智勇,蔡嘉(Cai Jinding,Lin Zhiyong,Cai Jia).基于等效电路参数的变压器油中糠醛含量判别法研究(Study on the discrimination method of furfural content in transformer oil based on equivalent circuit parameters)[J].仪器仪表学报(Chinese Journal of Scientific Instrument),2016,37(3):706-713.

[10] 黄云程, 蔡金锭(Huang Yuncheng,Cai Jinding). 油纸绝缘系统回复电压函数建模及拓扑结构辨识(Return voltage function modeling and topology recognition of oil-paper insulation system)[J]. 电力自动化设备(Electric Power Automation Equipment), 2016, 36(3):149-153.

[11] 许渊，刘有为，王文焕，等(Xu Yuan，Liu Youwei，Wang Wenhuan, et al.).大型电力变压器油纸绝缘含水量的介质响应诊断技术(Moisture content analysis of oil-paper insulation for large power transformers using dielectric response methods)[J].中国电机工程学报(Proceedings of the CSEE)，2012，32(33)：133-140．

[12] 彭积城，蔡金锭(Peng Jicheng, Cai Jinding). 油纸绝缘变压器老化特征分析(Analysis on aging characteristics of oil-paper insulated transformer)[J]. 电子测量与仪器学报(Journal of Electronic Measurement and Instrumentation)，2014,28(7):763-769.

[13] 廖瑞金,刘骁,刘捷丰,等(Liao Ruijin, Liu Xiao, Liu Jiefeng,et al.).现场变压器油纸绝缘时频域介电特征量提取及状态评估(Extraction of time and frequency domain dielectric characteristics and condition assessment for field transformer oil-paper insulation)[J]. 电力系统自动化(Automation of Electric Power Systems), 2015, 39(5): 94-100.

[14] 林智勇，蔡金锭(Lin Zhiyong, Cai Jinding). 油纸绝缘极化等效电路参数计算方法(Novel method to calculate polarized equivalent circuit of oil-paper insulation)[J]. 电机与控制学报(Electric Machines and Control)，2014,18(8): 62-66.

[15] Saha T K, Purkait P, Muller F. Deriving an equivalent circuit of transformers insulation for understanding the dielectric response measurements[J]. IEEE Transactions on Power Delivery, 2005, 20(1): 149-157．