智能优化算法自动生成计算机软件测试数据的方法

任 群

(亳州学院 电子与信息工程系，安徽 亳州236800)

随着软件应用规模越来越大，复杂程度越来越高，软件的质量和可靠性变得尤为重要[1-2]，计算机软件的数据测试也成了很多人关注的焦点[3-4]。在计算机软件的使用过程中，计算机软件本身的缺陷将会影响计算机的正常使用。计算机软件缺陷在软件开发的过程中是客观存在的[5-6]，如果不能及时发现软件的缺陷，就有可能导致计算机软件无法使用，甚至产生无法弥补的严重后果[7]。

基于上述问题，本文提出了基于智能优化算法的计算机软件测试数据自动生成方法。该方法能够在软件测试过程中自动生成测试数据，并自动对计算机软件测试数据进行优化测试。最后，对提出的方法使用Eclipse标准数据进行数据测试，结果表明，该方法可以提高计算机软件测试数据的自动生成效率，有利于改善软件的质量。

1 智能优化算法自动生成的测试数据模型

软件测试的目的是及时发现软件中存在的缺陷，并对其进行修正。在利用智能算法自动生成测试数据的过程中，需要从软件模块中提取度量元数据。利用回归、分类、聚类等方法找出度量元及其测试数据之间的相互联系，以相互联系为基准，对其建立测试数据模型，再通过基本模型对软件中的待测数据进行测试(如图1所示)。本文以智能优化算法自动生成的加权测试数据为基准，对计算机软件测试数据进行不同算法的对比实验研究。

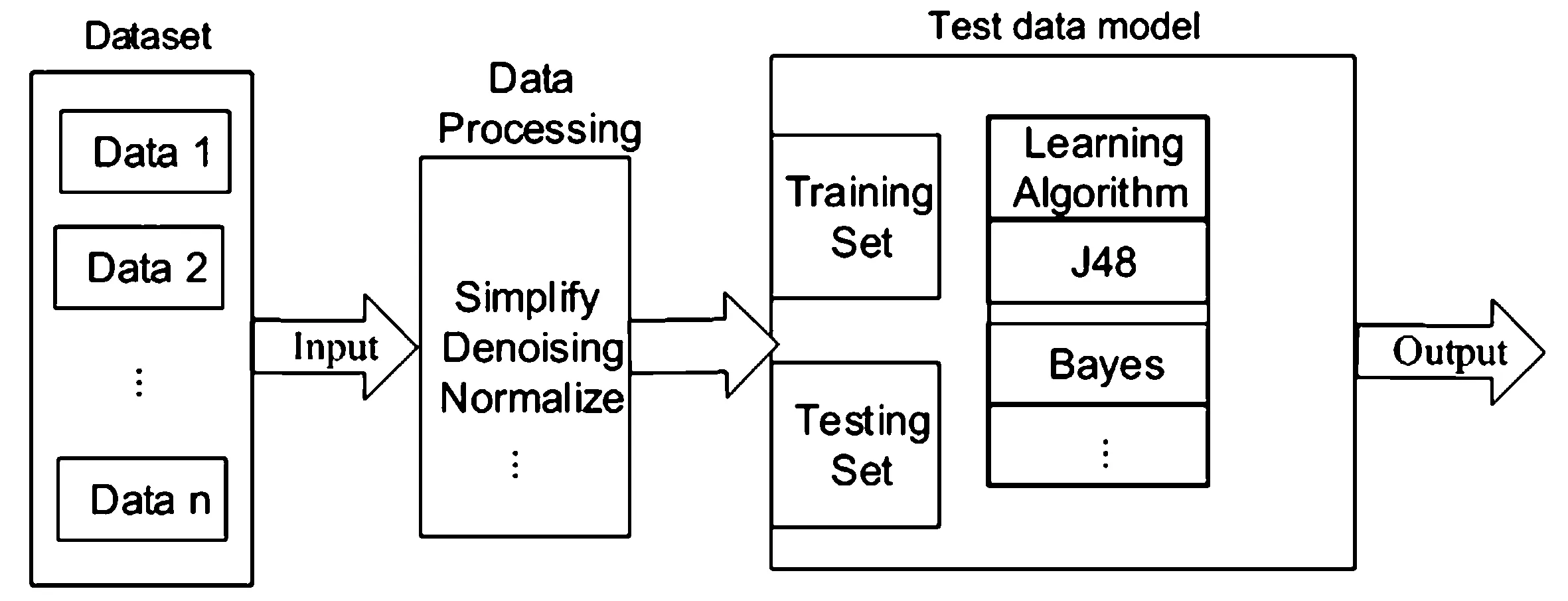
图1 计算机软件测试数据模型

2 智能优化算法自动生成的测试数据方法

2.1 计算机软件测试数据模型

本文中借鉴了Stacking技术，这是一种在行业中知名的集成推理技术。在Stacking框架中含有2层分类器，level-0表示的是基分类器，level-1表示的是元分类器。在软件数据测试中，第一步是对数据集进行预测，第二步是把基分类器中输出的结果作为输入数据通过元分类器进行输入，第三步，将生成的数据集作为新推理器的训练数据集，再利用数据测试算法对其进行测试。采用相对复杂的智能化算法进行计算机软件测试数据模型建立，利用此方法把属性子集应用到软件测试数据的建模之中，在数据丢失最小化的前提下提高模型的性能，以便减少测试时间。

定义1：属性A的数据增益率可用IGR(A)=IG(A)/I(A)进行表示，其中，IG(A)表示的是属性A的数据增益。IG(A)=entropy(S)-entropy(S,A)，表示的是划分之前数据的熵和划分之后数据的熵的差值。

设训练集S={S1,S2,L,SN}，在表达式中，Si含有一个属性向量，该向量可以表示为Xi=(xi1,xi2,L,xip)，同时Si还含有一个分类标签，该分类标签可以表示为ci∈C={c1,c2,L,cm}。式中，Xi表示的是含有度量向量的测试数据是否存在缺陷的标记，ci则对测试数据是否存在缺陷进行标记。如果设pi是S中属于类别i的比例，数据熵则用下式表示：

任何一个属性都有几个不同的取值，设Values(A)表示的是A中取不同值的集合，Sv表示的是集合S中所有属性A取值为v的集合，则可以得到：

本式表示的是基于按A划分后对S的元组准确分类还需要的数据量。

引入内在数据I表示的是训练集S用属性A进行划分后的数据集S'，若进一步划分，数据总量用下式表示：

数据增益率本质上是一种补偿措施，它可以有效解决数据增益中存在的问题。

2.2 用智能优化算法生成测试数据

获取计算机软件的测试数据时，应该确定合适的映射规则。二进制编码就是比较好的映射形式，它具有表达简洁、操作方便等诸多优点，可以提高智能优化算法的计算效率。根据数据类型的不同，所对应的编码映射也是不一样的。在进行计算机软件数据测试时可能会对其他参数产生影响。因此，需要将每个输入参数独立的编码，使其成为一个二进制位的参数，之后再将全部的参数连接起来，组成一个独立的个体，此处称之为多参数级联编码。具体如下：

级连之前：X1，X2，……,XN

b11b12…b1m，b21b22…b2m，……，bn1bn2…bnm

级连之后:b11b12…b1m，b21b22…b2m，bn1bn2… bnm

在进行解码时应该先从总码中切取n段，每段长度为m的数据链，再分别进行解码。

在本文中，采用智能优化转化公式：

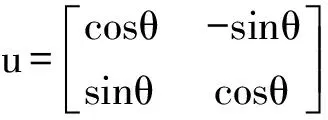
式中，θ为旋转角。

采用智能优化算法生成测试数据的步骤如下:

(1)初始化个体:扫描给定的路径，找出需要生成测试数据的变量，并为每个变量赋随机的0,1串，按照多参数级联编码原则，组成个体。

(2)计算适值函数值：根据构造的适值函数，分别计算每组变量的适值函数值，若满足终止条件，则转(4)步。

(3)改进个体:若没有满足条件的个体，则进行以下运算:

①按适值函数值选择下一代个体。

②解的交叉:从产生的个体中随机选择两个个体进行单点交叉，得到新个体，重复该步骤，直到所有个体均被选中为止。

③解的变异:在交叉后的个体中随机加入一些变异，产生新个体。

④转到第(2)步。

(4)拆分满足条件的个体:把每个变量对应的0,1串转换成十进制数，这些数据即为生成的测试数据。

(5)算法结束。

2.3 软件测试数据评价指标

对于本文设计的计算机软件测试数据评价指标主要有(area under ROC cure)、F-度量、精确度等。对于测试的结果可以采用表1所示的矩阵进行表示：

表1 评价指标

(1)精确度：precision=TP/(TP+FP)；

(2)召回率：recall=TP/(TP+FN)；

(3)F度量：F_measure=2×precision×recall/(precision+recall)；

(4)AUC：ROC曲线下面积。ROC曲线最初是用来对收益与成本之间的权衡关系进行描述的。AUC在区间[0,1]中波动，若模型越好，则面积越大(即AUC的值越大)。针对文中的软件测试数据，使用成本优化速度(Cost optimization speed, COS)作为评价指标，利用运算效率(Operational efficiency,OE)进行指标评价。

3 实验结果与分析

3.1 实验准备

本实验PC机的硬件条件是：Intel Core i3-4130 3.40GHzCPU,4GB内存。使用计算机软件为Eclipse，外部依赖项是weka.jar。实验数据主要来源于Eclipse标准数据，在这些文件中，有6个是ARFF格式的文件，这些文件不但收集了度量元，还收集了缺陷数目，在数据中，所包含的度量元包括以下四种：

(1)Name：表示的是数据对应的包名或文件名；

(2)Pre-release Defects：表示的是版本发布前半年内收集的缺陷数目；

(3)Post-release Defects：表示的是版本发布后半年内收集的缺陷数目；

(4)复杂性度量：指的是CK度量元与面向对象度量元；

(5)抽象语法树结构——抽象语法树的结点度量。

File级别与Package级别的数据，在结构上是有差异的。正因为这样，File级别的数据就只能测试File级别数据训练的模型，Package级别的亦是如此。我们使用File/Package中的数据进行测试。

3.2 实验结果

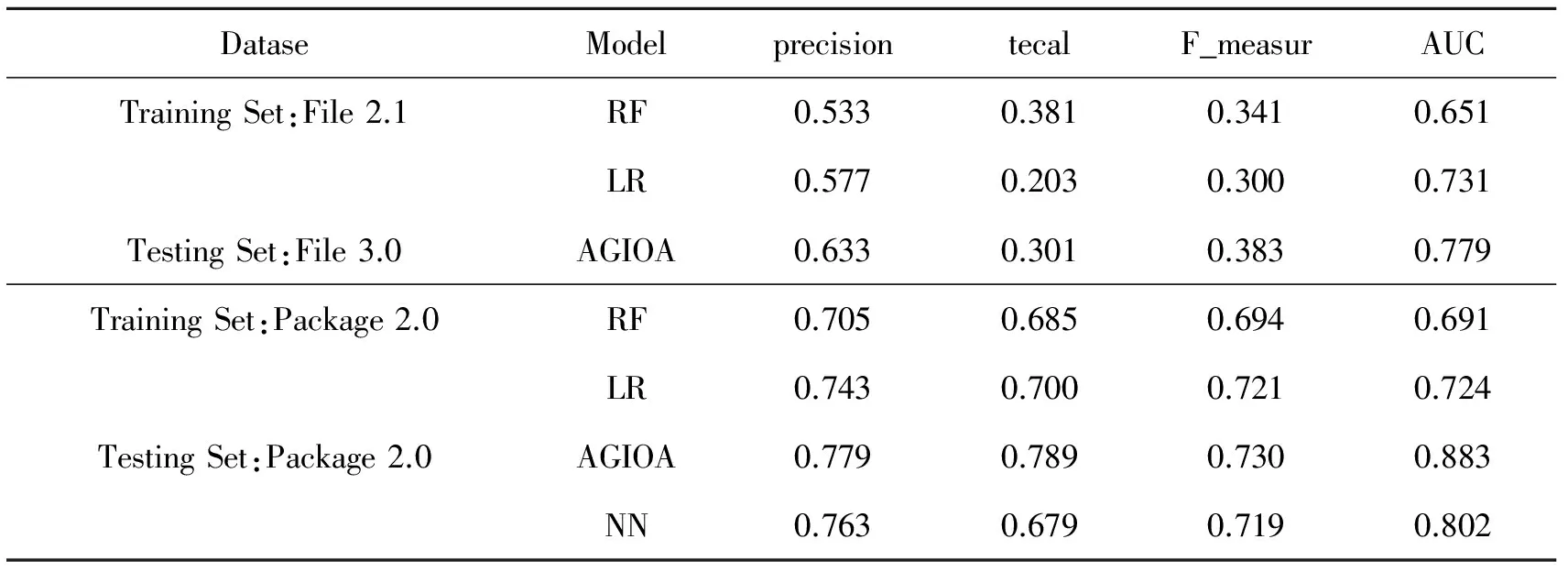
表2 不同的智能优化算法软件性能检测对比

先对数据进行一次测试，因为实验的结果太多，同时效果特别相似，因此只列出了一部分实验结果，见表2。为了方便表示，本文算法使用AGIOA表示，决策树算法使用RF来表示，逻辑回归使用LR表示，神经网络使用NN表示。

观察表2可知，逻辑回归算法的主要优势是测试精度高，但劣势也比较明显，就是召回率过低。决策树算法相对来说召回率比较高，但是测试精度并不高。神经网络算法在测试精度、召回率都不是很理想。而与其他三种算法相比，AGIOA算法在各方面均表现出了优越性。通常，测试数据模型越复杂，其综合指标越让人满意，但其耗费的时间也将越多。对于简单的测试，18次的实验，只要几分钟就能搞定；如果是算法过于复杂，18次实验则需要几个小时才能完成。这恰恰可以证实评价指标不同，算法也不会相同。

基于智能优化算法自动生成测试数据，将测试结果从大到小地进行加权计算，从而绘制出COS曲线与OE曲线，如图2所示。在COS评价中，计算机软件测试模型由于加入了回归度量，因此数据测试能力得到了提高。OE指标与单个算法测试比较相似，但以后的优化比较困难，原因是3种案例所使用的软件测试数据的自动生成算法原理几乎一致，因此很难为加权模型的数据测试提供有价值的数据。凡是采用智能优化算法自动生成算法的OE曲线，其斜率都接近1，换句话说，就是接近随机加权的结果。

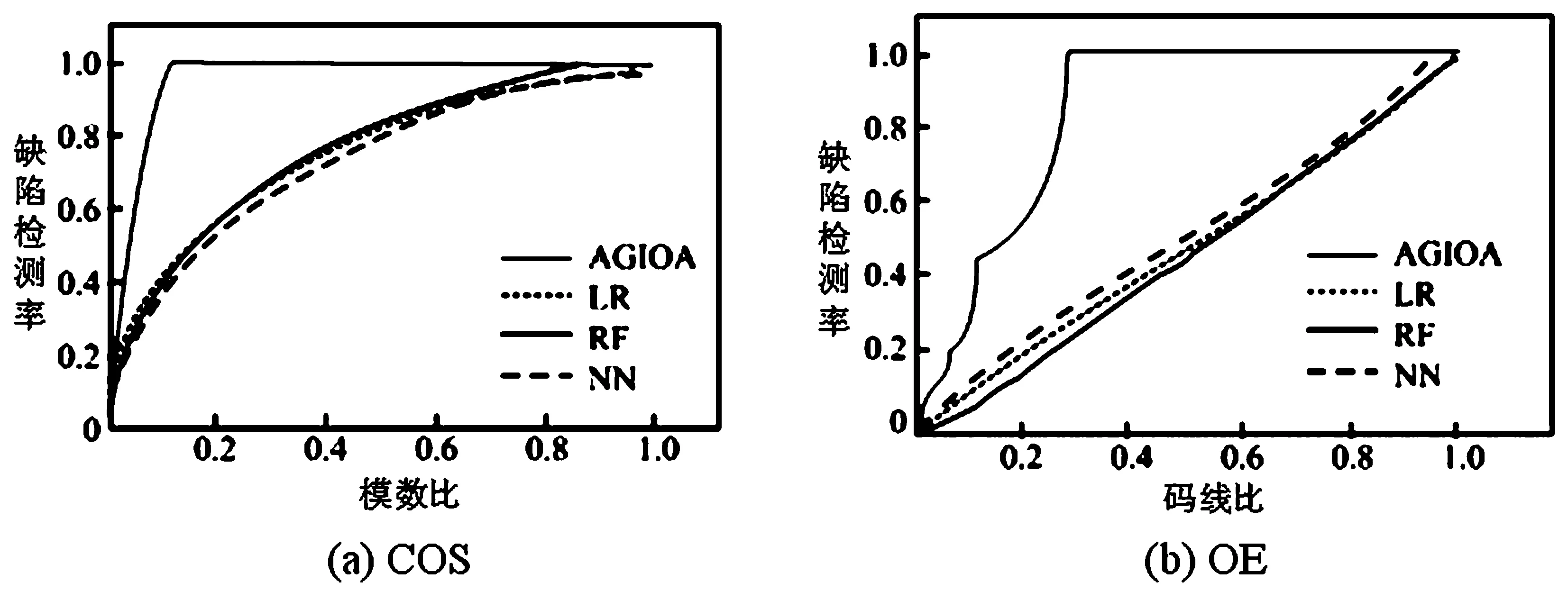
图2 智能优化算法自动生成的软件数据部分测试结果

4 总结

本文提出了基于智能优化算法的自动生成计算机软件测试数据的方法，该方法对所采集到的数据进行快速测试，将测试的结果与样本数据相结合，从而形成新的度量元，经过度量元处理后得到新数据。再利用智能优化算法对新的数据进行模型构建，所得的测试模型，经试验表明：该方法提高了软件测试数据生成效率，是一种较为理想的软件测试数据生成算法。

[1] Jiang, Z. M., & Hassan, A. A survey on load testing of large-scale software systems[J].IEEE Transactions on Software Engineering, 2015,41(11):1091-1118.

[2] Wang, M., Jia, H., Sugumaran, V., Ran, W., & Liao, J. A web-based learning system for software test professionals[J].IEEE Transactions on Education, 2011,54(2):263-272.

[3] Cotroneo, D., Pietrantuono, R., & Russo, S. Relai testing: a technique to assess and improve software reliability[J].IEEE Transactions on Software Engineering, 2016,42(5):452-475.

[4] Bohme, M., & Paul, S. A probabilistic analysis of the efficiency of automated software testing[J].IEEE Transactions on Software Engineering, 2016,42(4):345-360.

[5] Carlo, S. D., Prinetto, P., & Savino, A. Software-based self-test of set-associative cache memories[J].IEEE Transactions on Computers, 2011,60(7):1030-1044.

[6] Garousi, V., & Felderer, M. Worlds apart: industrial and academic focus areas in software testing[J].IEEE Software, 2017,34(5):38-45.

[7] Xu, J., & Xu, P. The research of memory fault simulation and fault injection method for bit software test[J]. IEEE, 2012,7(1):718 - 722.