莱顿弗罗斯特水滴振荡模式的影响因素及机理探究
胡子豪,任 宁,俞 熹
(复旦大学 物理系,上海 200433)
复旦大学代表队在2017年中国大学生物理学术竞赛(Chinaundergraduatephysicstournament,CUPT)中斩获亚军. 本文重点介绍了对CUPT课题5“Leidenfroststars”[1]的研究成果.
在莱顿弗罗斯特效应下,放置在高温表面的水滴能持续存在几分钟. 在特定情况下,这样的水滴会发展出振荡星形. 在高温表面上发生莱顿弗罗斯特效应的水滴有时会产生边缘呈星形状态的振荡模式. 基于该现象,文献[2-3]在一定的近似条件下求解了各个振荡模式的本征频率为
(1)
其中σ为水的表面张力系数,ρl为水的密度,R为液滴恢复到圆形的半径,n为星形角数. 将振荡的实际频率和该半径、角数下的本征频率理论值进行对比,可以为探究液滴振荡形成的物理机制提供思路. 大曲率凹曲面限制液滴的平动,能够使振荡模式表现出较强的规律性,本文将探讨一定温度下振荡模式的演化规律,并给出振荡模式随半径的分布及振荡频率随时间的变化. 文献[4]将液滴与高温表面之间的主要传热方式归结于热传导,而本文将从理论推导和实验出发说明热对流在该传热中的主导作用,并从伯努利原理出发对真实液滴的几何形状做出定性探讨,为液滴几何模型的修正提供思路.
1 实验原理
莱顿弗罗斯特效应下,液滴下表面迅速蒸发形成的蒸汽层将使液滴悬浮而不直接与表面接触. 悬浮液滴受到的摩擦阻力大大减小,其边界也因不再受到底面界面张力的束缚而处于非浸润的状态,因此易受外界扰动而产生复杂的运动.
重力场中悬浮液滴的几何形状由邦德数决定,定义为
(2)
其中Δρ为气液相密度差,σ为水的表面张力系数,L为特征长度. 邦德数表征液滴受到重力和表面张力的相对大小.Bo=1时,重力与表面张力平衡,定义此时的特征长度为毛细管长(忽略气体密度),即
(3)
莱顿弗罗斯特效应下液滴温度应始终接近沸点,实验测得为Tl=96 ℃,故表面张力系数取σ=58.9×10-3N/m,算得lC=2.5 mm. 由流体力学中的结论[4],液滴半径足够大时,其厚度为定值,且为毛细管长的2倍,即H=2lC=5.0 mm. 液滴半径较小时,表面张力的束缚使其不能产生振荡. 将真实液滴的几何形状进行适当简化,能够避免过于繁复的数学计算,有助于讨论该现象的物理本质. 故根据以上讨论,不妨将莱顿弗罗斯特液滴近似为扁圆柱形(图1),并在之后的讨论中沿用该近似.

图1 液滴的近似几何模型
2 实验设计
实验采用的加热装置为控温加热板,可设置温度为0~400 ℃. 测温装置为温度计和K型温差电偶,精确度为0.1 ℃. 实验采用5.0 mL注射器注入液体,注射器分度值为0.2 mL. 为减弱离子溶液的瑞利-泰勒不稳定性[4]对液滴形状的影响,用去离子水作为实验液体.
莱顿弗罗斯特效应下液滴受到的摩擦力极小,为了将水滴固定在曲面上某处进行观测,选用下凹的金属曲面进行实验. 2种曲面的实物图及尺寸图如图2所示.

(a)小曲率实物图 (b) 大曲率实物图

(c)小曲率尺寸图

(d)大曲率尺寸图图2 实验用曲面
3 结果及分析
3.1 振荡模式
实验中观察到的振荡模式如图3~4所示. 实验显示,大曲率曲面上液滴星形振荡的产生表现出更强的规律性,且能够在更大的半径下出现角数更多的振荡模式. 这是因为相比较小曲率曲面,大曲率曲面有以下优点:能够限制液滴的平动,能够让液滴边缘的形状接近圆形,曲面下凹能防止中央气泡升起破坏液滴形状. 因此,之后的研究都在大曲率曲面上进行.

(a)n=2

(b)n=3 (c)n=4

(d)n=5 (e)n=6图3 小曲率曲面上出现的振荡模式

(a)n=2 (b)n=3

(c)n=4 (d)n=5

(e)n=6 (f)n=7

(g)n=8 (h)n=9图4 大曲率曲面上出现的振荡模式
3.2 振荡的二维边界条件
在极坐标下对液滴某横截面上的边界进行讨论. 对于发生n角的振荡模式的液滴,将其在平面内旋转1周,将与原形状重合n次,这种性质可以通过cos (nθ)来描述;另一方面,不妨设液滴某一径向上边界质元的振动满足简谐函数. 由此便可以将液滴边界条件表达为
r=R+Asin (ωt+φ) cos (nθ).
(4)
用Mathematica对(4)式作图可以得到与振荡水滴十分相似的形状(图5),通过调节频率和振幅,可以使其与发生星形振荡的液滴完全重合,故认为振荡液滴的二维边界条件可以用(4)式表示. 瑞利将液滴的边界条件表示为[3]
r=α0+αncos (nθ)cos (kz),
(5)
对比(4)式和(5)式可知(5)式中αn即为(4)式中的Asin (ωt+φ)项;而cos (kz)则是出于对液滴不同厚度处振幅不相等的考虑.

(a)n=2 (b)n=3

(c)n=4 (d)n=5

(e)n=6 (f)n=7

(g)n=8 (h)n=9图5 振荡模式的二维边界
3.3 振荡液滴的本征频率
假设振荡的液滴具有以下性质:无黏性不可压缩流体;流速场无旋,存在速度势;液滴近似为圆柱形,并结合3.2中得到的边界条件,可以得到(1)式的本征频率表达式. 由(1)式中各变量的关系可知,对于角数为n的振荡模式,其本征频率fn仅由液滴半径R和角数n所决定. 测量了各振荡模式发生时液滴的半径和频率,并由(1)式得到数据拟合方程为
(6)

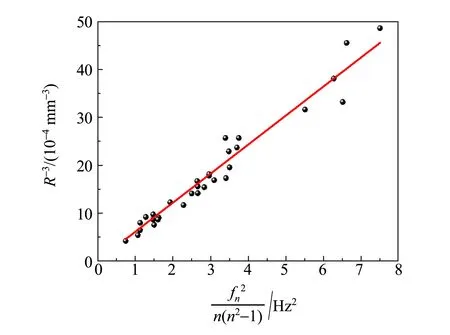
图6 振荡频率拟合
由图6中可以看出,1/R3=y较小的数据点距离理论曲线较接近,而y较大的数据点对本征频率理论值的偏离较大,这将在之后对液滴振荡产生的物理机制进行讨论时给出解释.
3.4 表面波与振荡的机理
大量实验显示,在液滴开始振荡之前的较短的时间内,其上、下表面常出现裸眼看来似乎静止的“光圈”. 用400帧/s的高速摄像机进行拍摄,发现“光圈”实际上是频率较高的表面驻波. 它产生自蒸汽层与液滴下表面之间的开尔文-亥姆霍兹不稳定性[2]表面波最终传播到整个液滴表面,进行叠加,稳定时便形成驻波. 仔细观察液滴由圆形进入振荡模式的过程,对星形振荡的机理做出以下解释:在一定条件下,表面波在包括液滴侧边缘的整个液滴表面发生稳定干涉而形成驻波,振幅原本很小的表面波叠加成为肉眼可见且具有一定规律的表面波,使得液滴表面出现“光圈”,如图7(a)所示;已有驻波存在的液滴边缘由于外界的微小扰动,从激励点产生了在边缘上向相反方向传播的行波,行波在边缘上进行叠加,如图7(b)所示;互相叠加的行波最终在边缘上形成了稳定的驻波,驻波的周期性体现为液滴的振荡,如图7(c)所示. 先前已有研究者将星形振荡的产生归结于液滴边缘产生的驻波[5],以上讨论可以给出更加明确的物理图像.

(a) (b)

(c)图7 水滴进入振荡模式的过程
通过测量发现,“光圈”的频率恰为星形振荡实际频率的2倍,故引入参量共振描述星形振荡产生的物理机制[6]. 无阻尼时的参量共振方程为
(7)
其中q为小量,可以描述系统在参变激励下对本征频率的偏离程度. 通过数学分析,可以知道(7)式成立的条件为
由于q为小量,因此参变频率对2ω0偏离不能过大. 如果考虑阻尼,如假设阻尼与系统的速度成正比,则又可得到
其中β为阻尼系数,这将使得对激励频率的选择变得更加苛刻. 通过类似的分析可知,参变频率Ω还可取2ω0/n,但由于范围过小而不稳定.
3.5 振荡模式的演化规律
某次实验中,振荡模式演化规律如图8所示,即随着液滴不断蒸发,其半径逐渐变小,液滴逐渐从大角数的振荡模式过渡到小角数的振荡模式(图8仅示意大致范围).

图8 振荡的演化规律
将不同温度下各15次实验中各振荡模式出现时的半径R为横轴,角数n为纵轴作图(图9),即可得到一定温度下角数随半径的分布关系:角数较大的振荡模式趋向于在半径较大时出现.

图9 振荡模式随半径分布
说明:1次实验中并非会总出现某个最大角数及以下所有角数的稳定的振荡模式(如1次实验可能只依次出现角数为8,6,4,3的振荡模式),但是图9给出了各振荡模式出现的大致半径范围,每次实验当液滴半径达到该范围时,即使不出现该振荡模式,也会形成类似于该振荡模式的形状(与角数为n的振荡模式类似是指,边缘出现角数为n,但是各角的振荡不同步,或者振荡同步但是各角之间的大小差异较大,因而不形成稳定的振荡模式). 考虑到蒸汽层的不稳定性及参量共振对激励频率要求之苛刻,这是不难理解的.
实验中有时会在n角振荡的前后分别出现n-1角的振荡模式. 换句话说,有时会在较大的半径出现角数较小的振荡模式. 这是因为参量共振允许Ω≈2ω0/n,但是由于这时频率的允许范围过小,这些振荡模式都会很快衰减而不稳定. 图10所示为1次实验中振荡刚出现时频率的变化(n=7的模式出现2次),图10中标出了各点对应的振荡模式.

图10 1次实验中的频率变化
由图10可知,液滴振荡频率随时间呈总体下降,局部上升的趋势. 结合(1)式来理解:在某一振荡模式的持续的短时间内,角数n不变,液滴半径R因蒸发而减小,故液滴振荡的频率增加;时间较长时,液滴的角数n随半径减小由大变小,其频率的影响超过半径R,导致了振荡频率的减小.
以上分析也可以对星形振荡的“不稳定性”做出定性解释:由于蒸发半径不断减小,一种振荡模式要发生并持续下去,就要求其振荡频率在一段时间内保持上升;而实验规律显示振荡频率总体呈下降趋势,恰与维持振荡模式所要求的条件相反. 这就导致各种振荡模式不易发生,即使发生,也不能长时间维持.
3.6 莱顿弗罗斯特液滴的热力学模型
考虑到莱顿弗罗斯特效应发生的热力学背景,建立热力学模型以探讨温度对该现象的影响十分必要. 这里主要探讨液滴与热表面之间的传热方式. 依然用圆柱模型做近似处理,可得底面积S、体积V与半径R的关系:S=πR2,V=2SlC. 考虑到蒸汽层一般是热的不良导体及其流体的特性,认为热传导为二者间主要的传热方式,由此可以列出以下关系:
J=kSΔT,
(8)
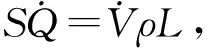
(9)
其中,J为热流密度,k为对流传热系数,L为水的潜热. 可解得半径随时间变化关系为
(10)
对(10)式用直线进行拟合,结果如图11所示.

图11 半径随时间变化拟合结果
由于对流传热系数难以确定,从理论上计算斜率也相当困难,但是拟合度0.99线性良好,说明(10)式能够刻画短时间内半径的变化结果,由此可以说明热对流模型的正确性. 需要注意的是,当时间过长时,由于液滴的半径等条件发生变化,对流传热系数α发生较明显的变化,导致线性关系不再成立.
3.7 真实液滴的几何形状

(11)
即某点的气体溢出速率与该点到圆心的距离成正比,蒸汽层越靠近边缘处流速越大. 由伯努利原理,气体流速大处压强小,因此蒸汽层边缘压强小于中心处压强,这将导致蒸汽层的中心处较厚而边缘处较薄,导致液滴中间较薄而两边较厚(图12),而非呈现出之前假设的理想的圆柱体形状.

图12 真实液滴的几何形状
4 结 论
讨论了莱顿弗罗斯特液滴的动力学特性,提出了简化的液滴几何模型,通过软件做图分析了振荡的二维边界条件(4)式,这是求解液滴本征频率的一个重要条件. 通过比较振荡的实际频率与本振频率理论值以及观察和测量伴随振荡出现的表面波,推测并验证了液滴的振荡是表面波在边缘叠加形成的驻波,并引入参量共振描述液滴振荡的机理. 参量共振可解释实验中诸多现象:
1)表面波的频率为振荡频率的2倍,这是因为参量共振方程的参变频率为本征频率的2倍.
2)半径较大时,实际频率与本征频率接近,这是因为参量共振频率对本征频率的偏离是小量;而半径较小时,振幅占半径的比重过大,不满足振幅偏离为小量的条件,振荡体现出非线性振动的特性,因而偏离本征频率.
3)稳定的振荡模式比较难出现和维持,因为参量共振允许的参变频率的范围很小.
4)有时较大半径的液滴出现角数较小的振荡模式,因为参量共振允许Ω≈2ω0/n,但不稳定.
用热对流模型推导了液滴半径随时间的变化,实验值与理论符合良好. 从蒸汽层流速出发证实真实液滴的几何形状中间较薄而两边较厚.
[1] 陈玥,周子淇,林美妤,等. 振荡“星形”水滴的实验研究[J]. 物理实验,2017,37(11):36-41.
[2] Lamb H. Hydrodynamic [M]. 6ed. Cambridge: Cambridge University Press, 1916:436-437,473-475.
[3] Rayleigh L. On the capillary phenomena of jets [J]. Proceedings of the Royal Society of London, 1879,29:71-97.
[4] Soto D. Non-wetting drops: from impacts to self-propulsion [D]. Pierre and Marie Curie University, 2014:28-42.
[5] Snezhko A, Jacob E B, Aranson I S. Pulsating gliding transition in the dynamics of levitating liquid nitrogen droplets [J]. New J. Phys., 2008,10(2):043034.
[6] 梁昆淼,鞠国兴. 理论力学[M]. 4版. 北京:高等教育出版社,2009:299-302.

