基于磁致旋光效应测量有限长通电螺线管轴向磁场分布

庄浩丽,韩俊彦,林佳佳,李苑喆,张舒婷,曾育锋

(华南师范大学 物理与电信工程学院,广东 广州 510006)

目前，研究有限长通电螺线管空间轴向磁感应强度分布通常基于霍尔效应，用特斯拉计或半导体磁敏元件等间隔伸入通电螺线管内部测量各位置的磁感应强度. 霍尔效应的产生需要在垂直于外磁场的方向上通以电流，电流的磁效应会使霍尔元件的附近形成磁场，与通电螺线管内部的磁场叠加，由此会给测量结果带来误差. 考虑到倍频法研究法拉第磁致旋光效应[1]的精度较高，而且基于光学原理的测量方法不会在通电螺线管内部产生附加磁场，所以笔者尝试用法拉第磁致旋光效应探究有限长通电螺线管空间轴向磁感应强度分布.

1 理论分析

1.1 有限长通电螺线管空间磁场分布

设有限长通电螺线管的长度为L，半径为R，单位长度的匝数为n，电流为I，有限长通电螺线管如图1放置，由于螺线管具有对称性，只研究取yOz平面的磁场分布，y和z分量分别是径向和轴向分量. 根据磁场强度矢量与磁矢势的微积分关系，求出空间点的磁场，然后再通过椭圆积分,利用Mathematica数学软件从理论上画出了通电螺线管轴向空间点磁感应强度的分布，如图2所示[2].

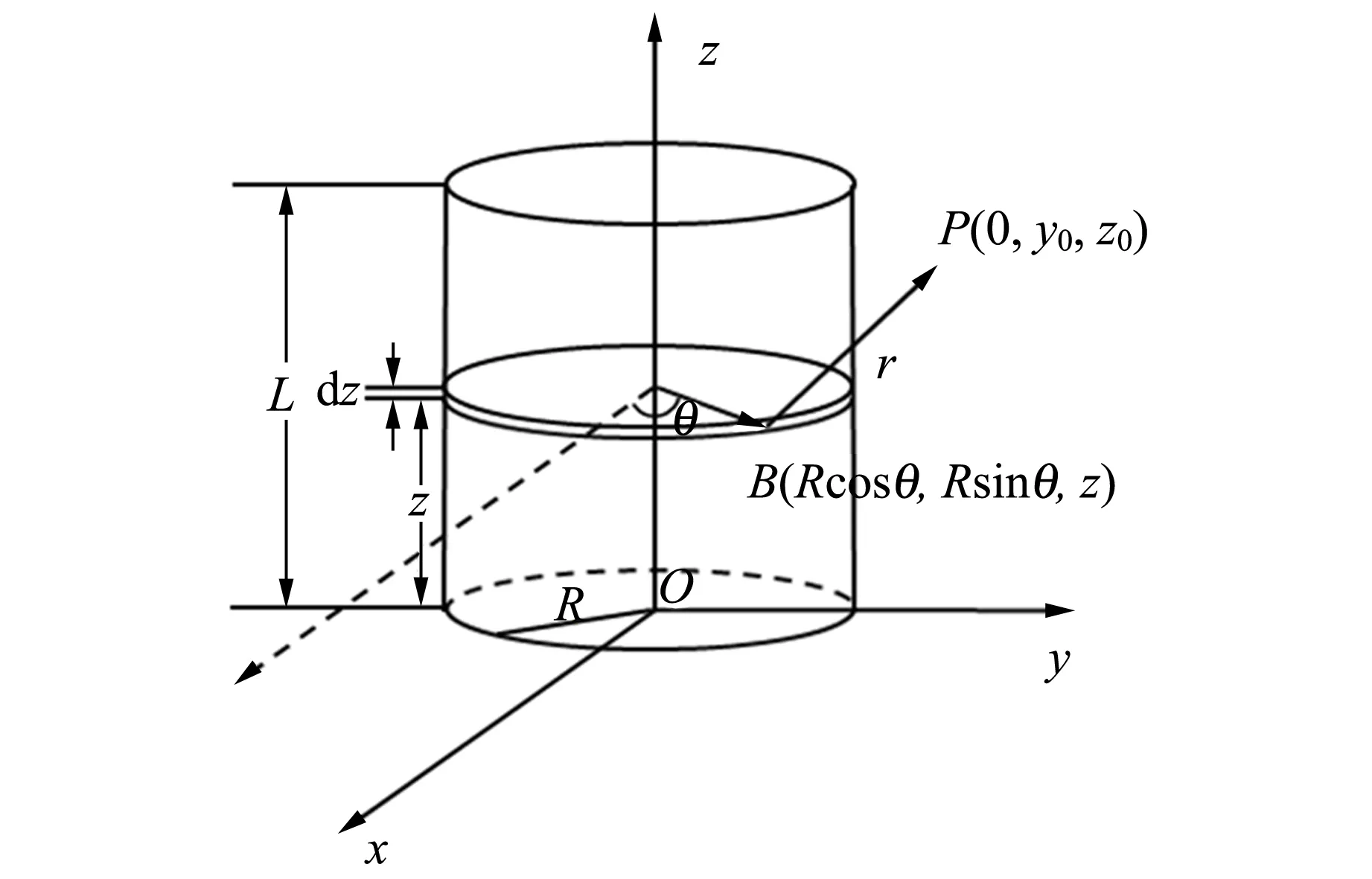
图1 螺线管示意图

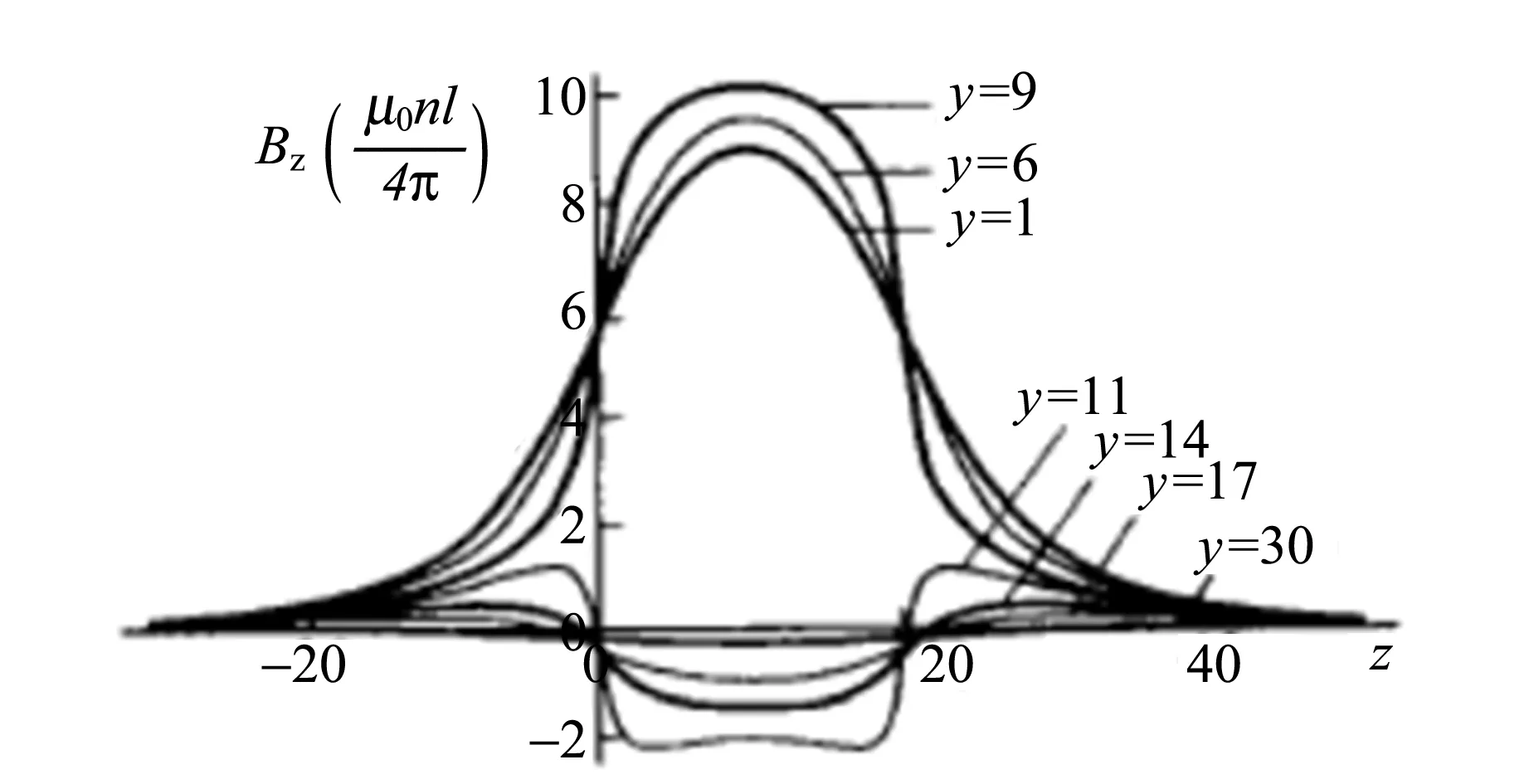
图2 固定y，轴向分量Bz与z的关系

1.2 法拉第效应

法拉第磁光效应是指：线偏振光通过放置在磁场中的磁光玻璃，沿着磁场方向传播时，光的偏振面发生偏转[3].

已知对于顺磁介质和抗磁介质，磁场不是很强时，偏振面的旋转角θ与光在介质中通过的路程L、外加磁感应强度B在光传播的方向上的分量成正比

θ=VBL,

(1)

比例系数V由物质和工作波长决定，表征物质的磁光特性，称为费尔德常量，对于顺磁介质和抗磁介质，V为常量.

而对于有限长的通电螺线管的轴向磁场分布存在分布不均匀的情况，所以磁致旋光效应是介质长度内的积分效果，即

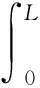
(2)

其中B(z)可根据文献[2]，令y0=0，即可得到有限长通电螺线管z轴的轴向磁场分布为

(3)

1.3 倍频法

在法拉第磁光效应实验中发现，晶体在调制励磁线圈正弦交变磁场的作用下产生交变的振动面旋转，当起偏器与检偏器振动方向平行或者正交时，可从示波器观察到频率为调制信号2倍的倍频信号，这就是磁光调制的倍频现象[4]. 通过数学推导和实验分析可以证明当偏振夹角为0和π/2时会发生倍频现象.

实验利用法拉第效应实验仪、双踪示波器，分别在样品不外加磁场以及加入磁场下，读出出现倍频现象时测角仪的度数，2次读数的差值为交流磁场B所引起的法拉第旋转角.

2 实验系统及测量结果

实验测量光路如图3所示，样品在通电螺线管内移动的示意图如图4所示. 实验中，选取介质长度为10.0 cm的重火石玻璃样品. 向右为正方向建立一维坐标，设坐标0刚好是螺线管左边界的起始点，以样品的左边界为参考点.在磁场恒定的情况下，每移动1 cm，记录1次样品的偏转角，直至样品完全移到螺线管外，得出样品在不同位置时偏振光经过样品后的偏转角随相对位置变化的关系曲线，改变磁场强度，重复实验. 本实验通过改变通电螺线管的电流来改变磁场强度，如图5所示.

再次测量样品完全在通电螺线管内移动时的数据，得到样品在相对位置在0～10 cm处时偏振光的磁致旋光偏转角随相对位置的变化关系图(如图6所示). 由图6可以看出在有限长通电螺线管的内部，轴向磁场先增大后减小，在螺线管中间最强，两边稍弱，但仍可近似看作均匀磁场，符合文献[2]中数值计算的结果，如图2所示.

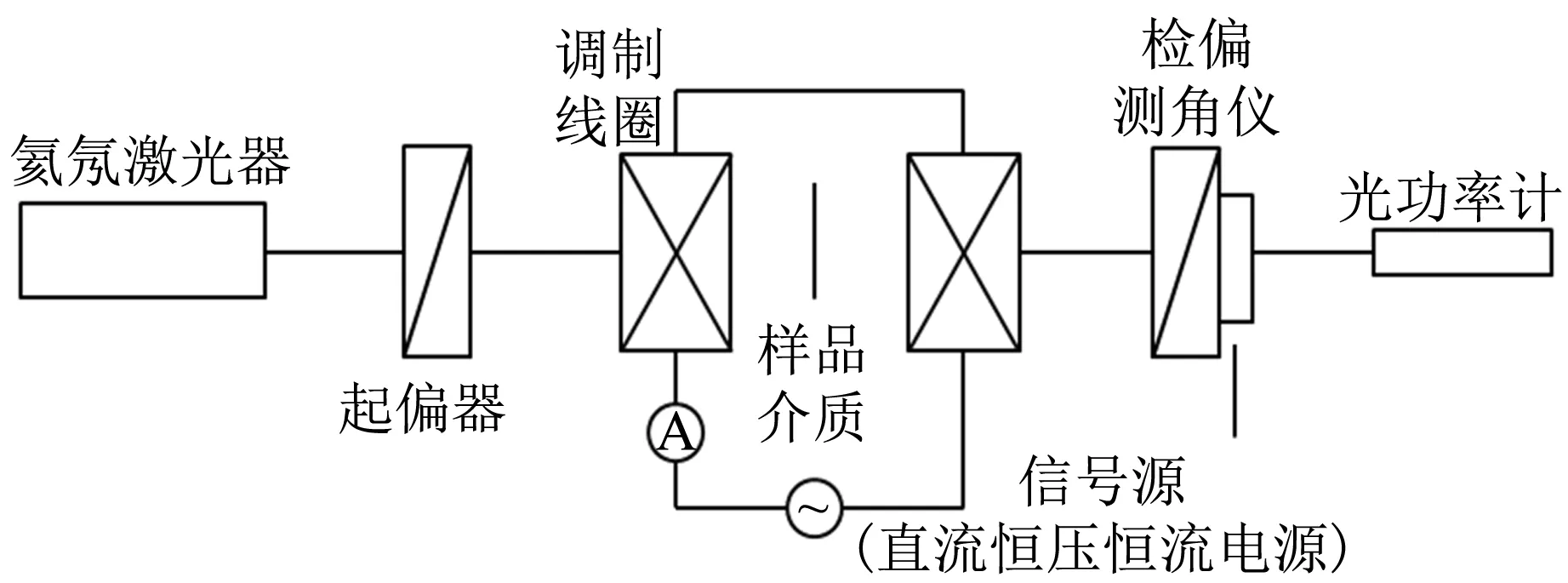
图3 测量光路图

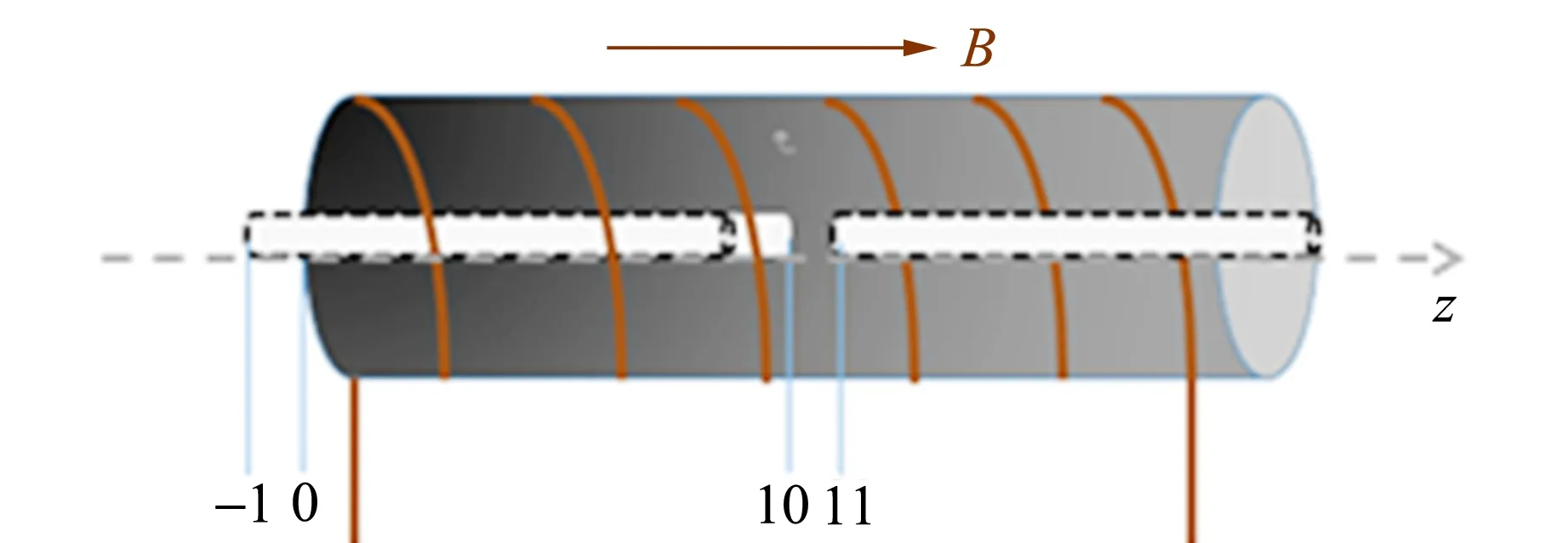
图4 样品在通电螺线管内移动示意图

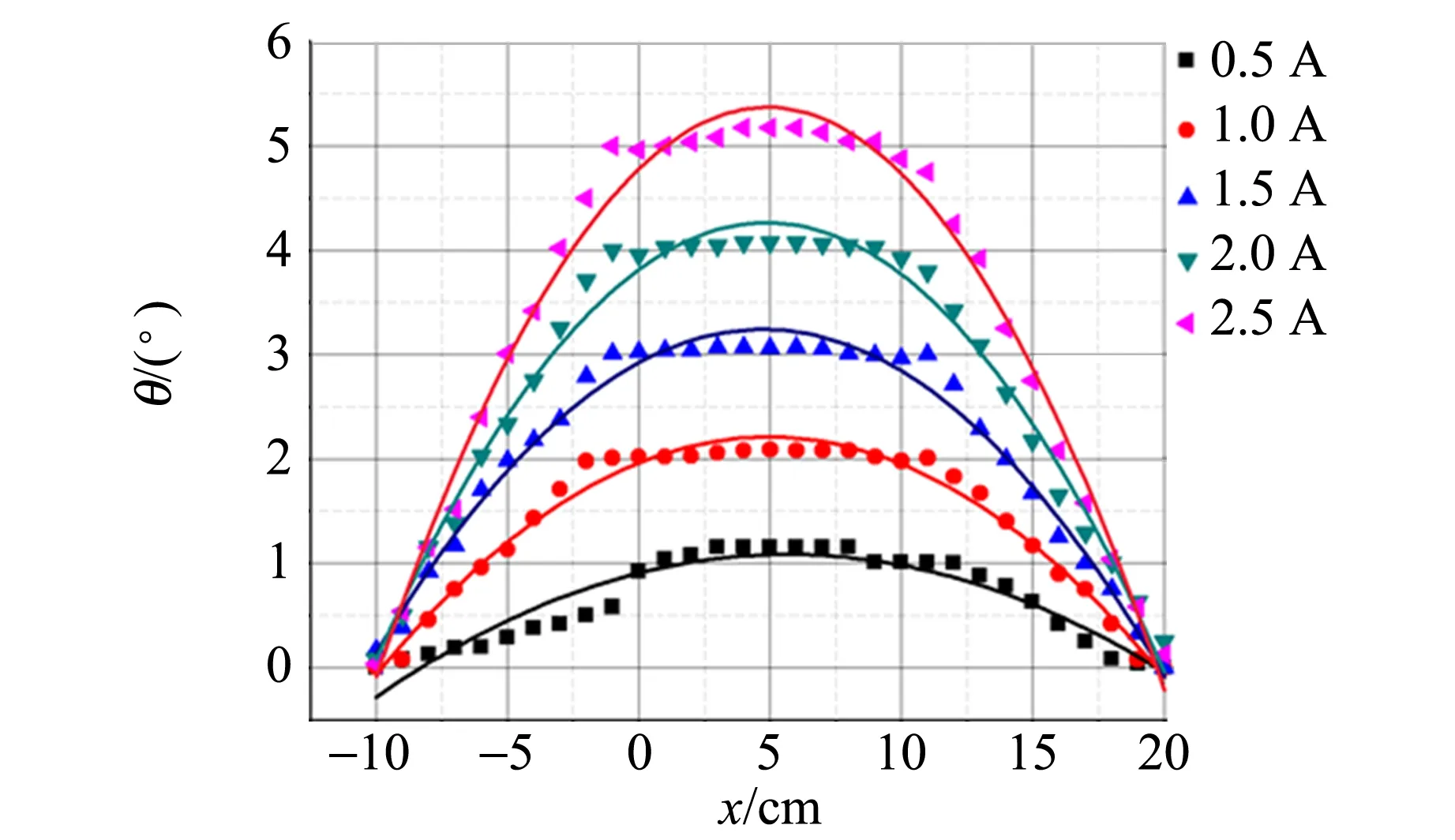
图5 不同电流下磁致旋光偏转角随相对位置的变化关系图

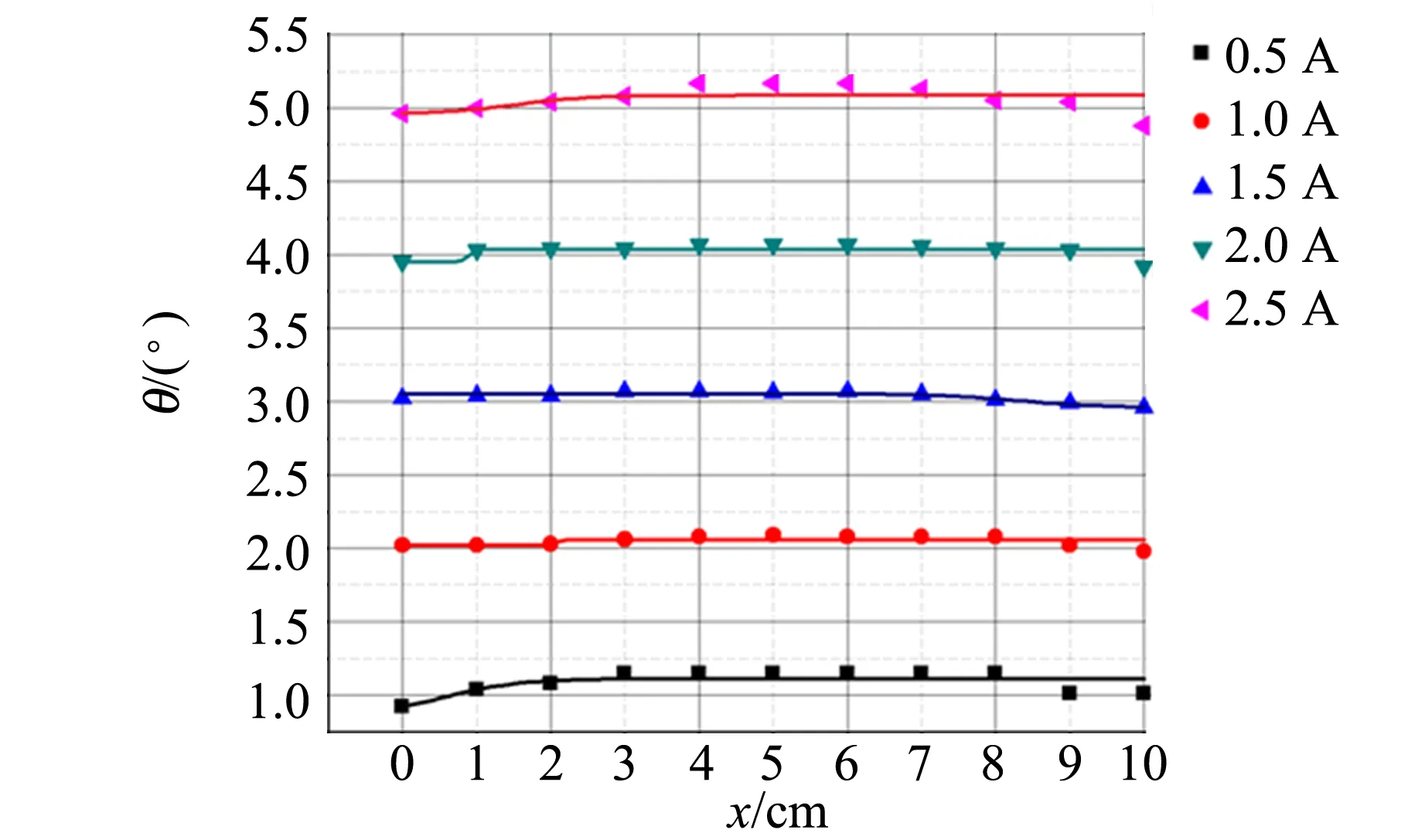
图6 不同电流下磁致旋光偏转角随相对位置的变化关系图

由于通电螺线管两端的轴向磁感应强度分布是对称的，故只分析一侧数据. 提取图像中的后11个点来研究在有限长通电螺线管外的轴向磁感应强度的分布.若通电螺线管外部不存在磁场，所有的点都应落在曲线第1个点与点(0,20)相连的直线上或均匀分布在直线两侧，但实际上所有点几乎都会落在直线的上方(图7)，说明在螺线管外的介质仍然受到了轴向磁场的作用.设在螺线管内的介质的长度为L′，由于外部微弱磁场的作用，使有效长度L略微大于L′，根据θ=VBL，θ会略微偏大，则证明通电螺线管外部仍有轴向磁感应强度分布，但相对于螺线管内部的磁感应强度小得多，同样符合图2的数值模拟结果.偏转角θ与样品的相对位置不严格成线性是螺线管内部与外部的磁场与介质有效长度共同影响的结果.

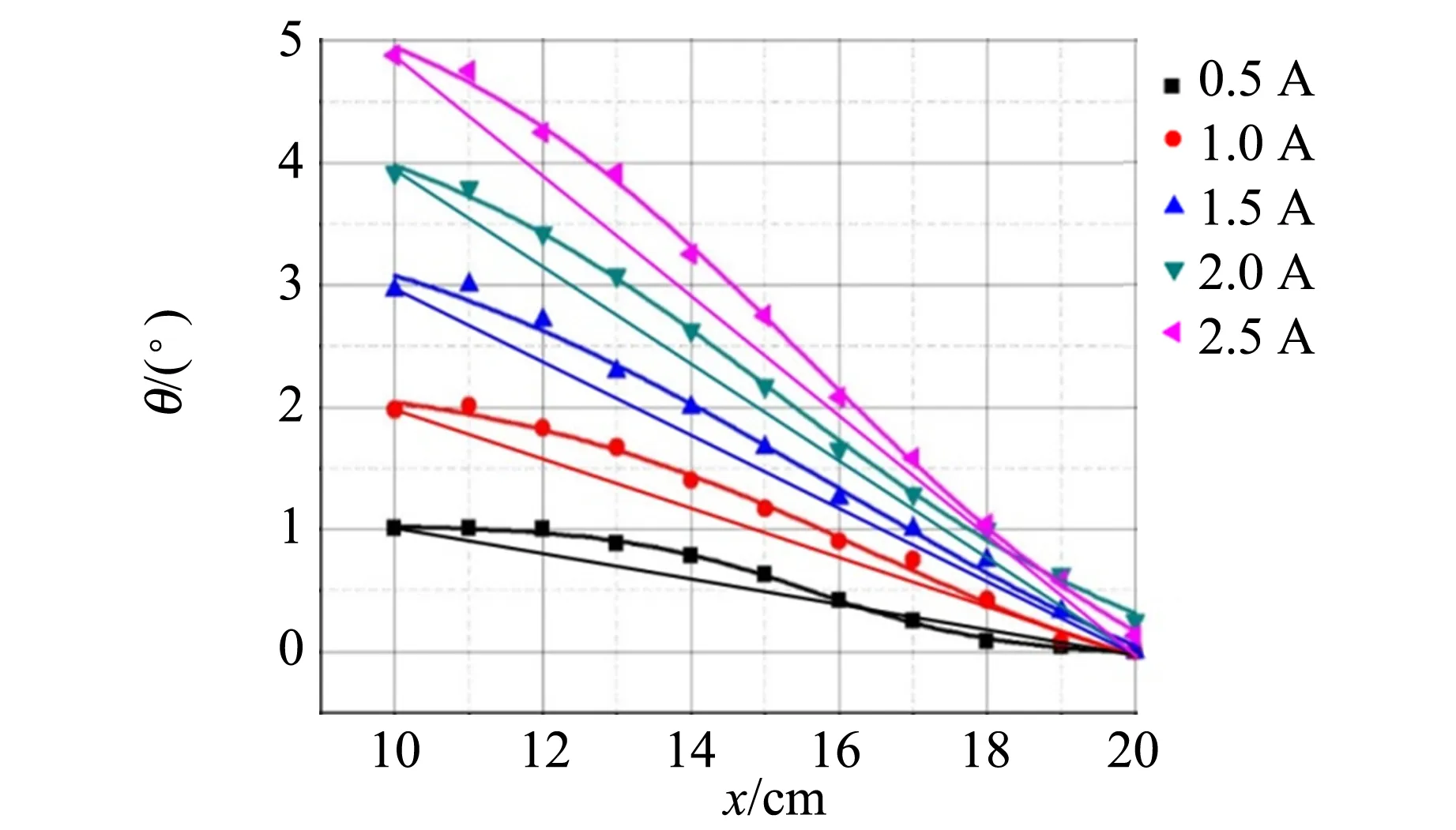
图7 样品在螺线管10～20 cm处时偏振光的磁致旋光偏转角随相对位置的变化关系图

3 结束语

基于磁致旋光效应原理，探究验证有限长通电螺线管空间轴向磁场分布的情况. 经对图像的分析可知，有限长通电螺线管内部的轴向磁场近似是匀强磁场，但两端磁感应强度会略微减弱；通电螺线管外部仍然有轴向磁场分布，但是磁感应强度随离螺线管距离的增大而快速减小.

[1] 吴思诚，王祖铨. 近代物理实验[M]. 北京：北京大学出版社，1995.

[2] 惠小强,陈文学. 有限长通电螺线管空间的磁场分布[J]. 物理与工程,2004,14(2):22-23，25.

[3] 钟锡华. 现代光学基础[M]. 北京：北京大学出版社,2012.

[4] 陆遥,陈铭南,倪晨. 法拉第效应实验中倍频现象的研究[J]. 大学物理,2010,29(4):60-62.

[5] 底楠,徐晓鹏. 关于磁光调制倍频法的讨论和改进[J]. 物理实验,2007,27(5):10-12，16.

[6] 刘公强,刘湘林. 磁光调制和法拉第旋转测量[J]. 光学学报,1984,4(7):588-592.

[7] 孟甜甜,符照森,刘辉,等. 基于磁光调制原理的高精度偏振角测量方法模拟与实验研究[J]. 西北大学学报(自然科学版)，2011，4(6)：965-968.

[8] 侯昭武. 通电螺线管空间点的磁场[J]. 广西民族学院学报(自然科学版),2005,11(1):105-108.

[9] 罗浩,向泽英,谢英英,等. 霍尔效应法测磁场实验误差研究[J]. 大学物理实验,2015,28(4):99-102.

[10] 渠珊珊,何志伟. 基于霍尔效应的磁场测量方法的研究[J]. 电测与仪表,2013,50(10):98-101.

[11] 蔡伟,伍樊成,杨志勇,等. 磁光调制技术与应用研究[J]. 激光与光电子学进展,2015,52(6):24-33.

[12] 孙可芊，李智，廖慧敏，等. 霍尔效应中副效应的研究[J]. 物理实验，2016，36(11)：36-40.