沉默中静待发现探索中突破思维——一道数学题的教学实践和反思

◇李保妹

在北师大版教材三年级下册“面积”单元的练习课上，我尝试出示了练习册上有关“组合图形的面积计算”的一个题目：把两张边长分别为6cm和3cm的正方形纸片拼成如图1所示的图形，求所拼成图形的面积。

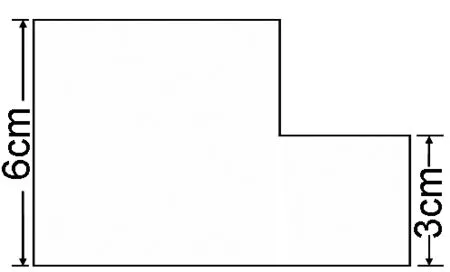
图1

按照正常的教学进度，组合图形的面积是在五年级学习的，对于三年级的学生来说肯定是有一定难度的，学生会有什么样的表现呢？教研组商议后，我们决定在课堂中试一试。但考虑到学生的年龄特点，在交流前，我预设了以下3种常规方法（如图 2～4，算式略）。

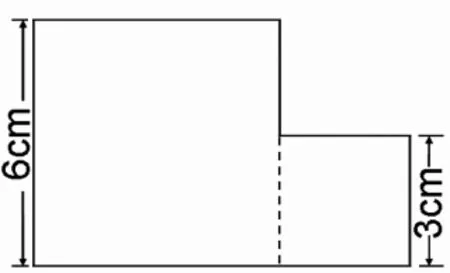
图2

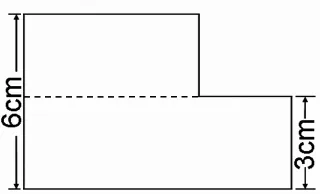
图3

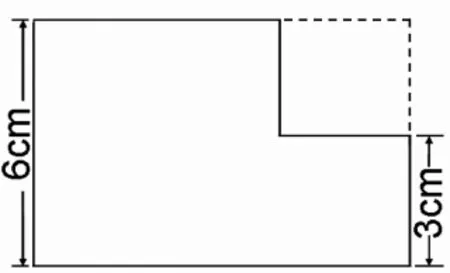
图4

孩子的智慧在指尖上。课前我让学生准备了本题的相应纸片和安全剪刀，鼓励学生使用这些学具，动手操作想办法求出面积。我想，结果肯定不会超出我预设的3种。

出示题目后，教室里一片安静。孩子们开始思考，有的写，有的画，还有的在剪拼……正当我准备带着大家分析时，有学生举手了。一个学生是这么想的：在两个正方形交界处画一条线段（如图2），这样就把整个图形分成了一大一小两个正方形。这不正是我要讲的第1种方法吗？我心里暗暗高兴。

也许受了这个学生的启发，只沉默了一小会儿，其他学生又发现了第2种、第3种方法。

我预设的3种方法学生都探索出来了，我正准备总结、进行巩固练习时，耳边忽然响起了一个声音：“老师，我还有不一样的方法。”难道还有别的方法吗？

他的想法是：6－3＝3（cm），3×3×5＝45（cm2）（如图5）。虽然数据有一定的巧合，但对三年级学生来说，确实是一种很巧妙的方法！我备课时怎么就没有想到呢？那一刻，喜悦伴着意外从我心底直涌上来！我向这个学生竖起了大拇指，对他说：“你的思路太精彩了！”其他学生在弄明白这种思路之后，一边感叹着这种方法的高明，一边自发地报以热烈的掌声。

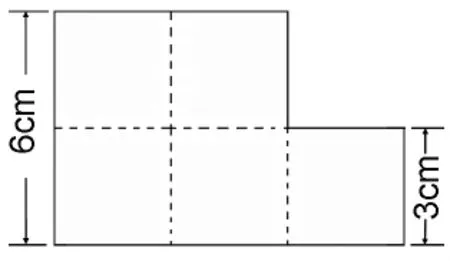
图5

面对此种情形，我冷静地想：求这个图形面积的方法是不是还有呢？于是我临时改动了教学安排，把剩余的时间全都留给学生探索新方法、展示新思路。我说：“同学们，这个图形的数据很特别，求它的面积的方法会不会还有呢？你们继续把图形分一分、割一割或补一补，惊喜说不定会悄悄来临哦！”

又是一小会儿的沉默，果然又有人想出了新方法，有了新的突破（如图6）。

还真是好方法！我再一次感到意外和喜悦，因为有人已经知道运用转化思想来解题了。我情不自禁地带头给这个学生鼓起了掌。

掌声刚落，又一个声音：“老师，我也想出了一种办法。”（如图 7）

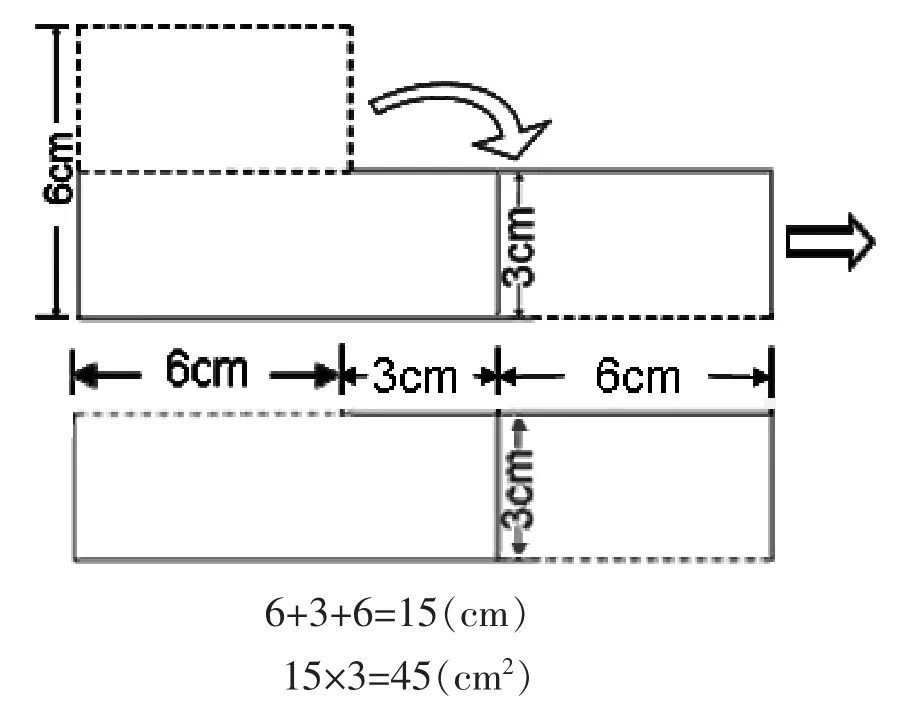
图6

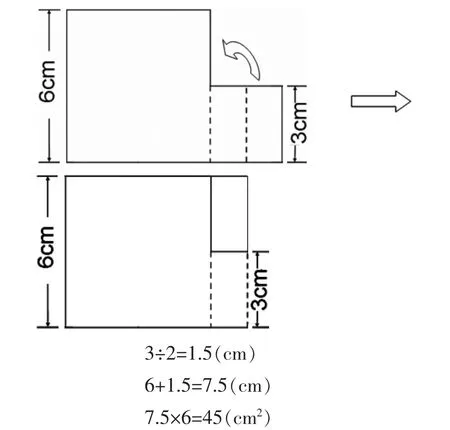
图7

真是妙哉！妙哉！

课已经上完了，我的心情却久久不能平静，课堂中精彩的一幕在我脑海中一次次浮现。本以为孩子们不容易解决的一道数学题，他们竟想出这么多不同的解法，孩子们的潜力可真大啊！

在教学中，我们绝不能轻易打破学生静静思考的稍许沉默，要给足他们探索的时间和空间，不能低估学生的能力，要相信他们，合理有效地利用好生成的资源，灵活地调整教学安排，最大限度地挖掘学生的潜力，组织学生充分交流和思维碰撞，尽显数学思维之魅力。