无线传感器网络环境下能量有效的虚拟坐标构建

杨 浩

(盐城师范学院 信息工程学院， 江苏 盐城 224002)

1 引 言

无线传感器网络(Wireless Sensor Network,WSN)由多个传感器构成，从而导致数据传输路径多样化，使得如何准确有效地为构建路由成为一个至关重要的问题[1-3].众所周知，WSN中的传感器资源，尤其是能量，是非常有限的.因此，在建立路由的过程中应该尽可能减少传感器的能量消耗.另一方面，贪婪搜索方式能快速实现数据传输.因此，直观上可以采用贪婪策略来进行无线传感器网络的路径搜索.它的基本思想是网络中的节点根据地理空间的位置远近，直接将其邻居节点作为转发节点，直至传输到sink节点.根据这一方式，仅利用节点的局部信息，就可以建立出节点到终端的路由[4,5].然而，在无线传感器网络中，感知单元不稳定性导致网络中的连接关联及其不稳定.为此，我们可以利用虚拟坐标系统[6,7]来解决这一问题.具体来说，就是可以将WSN的拓扑图提取出来，将传感器作为图中的节点，相应的通信链路作为连接边，这样就可以将传感器转化为成虚拟坐标.需要注意的是，在转换过程中要保持对应的保角等价关系.之后，利用贪婪搜索就可以很容易为这些传感器构建起合适的路由[7].在实际应用中，贪婪搜索方法一般会遇到一个常见的问题—空洞.具体来说，当传感器在传输过程，若其附件没有可联通的其他节点时，即存在所谓的空洞现象时.在这种情况下，路径搜索显然就会被迫中止，从而导致路由构建的失败.随着网络节点的增加，这一情形显然很容易发生.空洞问题的出现是由于传感器物理拓扑关系导致的.

为解决上述问题，本文拟基于双曲Ricci流构建虚拟坐标.我们基于离散黎曼度量计算三角网格的边界长度.在这一过程中，为解决实际网络拓扑可能存在空洞的情形，我们设计一个映射，使得该映射既是保角的又不会陷入空洞.为此，本文用上半盘模型计算双曲距离，并选择合适的莫比乌斯变换.利用所得到的虚拟坐标，无线传感器网络中的每个节点只需要传输所采样的数据给其邻居节点，然后利用一般贪婪搜索算法就可以很容易地得到合适的路由.

在实际应用中，将整个网络进行坐标转换需要消耗大量能量.为减少转换过程的能耗，本文进一步提出一个优化方法.它的基本思想是将网络拓扑进行区域划分，并构建一个概率性的候选集来选择合适的待映射节点.实验证明，我们的优化方法可以在保证有效构建路由的情况下有效地降低转换能耗.

2 理论背景

本节主要给出相关基本概念，包括黎曼度量、环包度量、高斯曲率和曲面Ricci流等.

2.1 基本概念

2.1.1 黎曼度量

黎曼度量[7]主要用于度量黎曼流形上曲线的长度.假定曲面A在欧拉空间中，则它的第一基本形式(first fundamental form)就是黎曼度量.假设存在两个正切向量a1=(dx1,dy1),b2=(dx2,dy2)且它们相交于切平面的一个点h∈A，则通过张量度量上述两个向量的夹角，得

(1)

假定t'是A上的另一个黎曼度量，f(c)是一个方程，若t'=e2f(c)t，则可以认为这两个黎曼度量是保角的.利用等式(1)，可以得到任意两个正切向量的角度.实际上，方程f(c)可看作是一个保角因子，用于测量给定区域的变形程度.

需要注意的是，如果曲面M的曲率满足以下关系：

(2)

其中，∂M表示曲面M的边界，dA表示曲面A的区域，dL表示曲面M的边界长度，χ(M)<0表示曲面M的欧拉特征数.

2.1.2 环包度量

为了近似拟共形映射问题，Turston提出了环包度量，它可以把度量metric和边缘相关转化成metric和vertex 相关[8,9].具体来说，假设存在一个网格空间，每三个顶点组成一个关联片，且每个顶点连接到一个圆.每个关联片中，对应的两个圆是相交的.因此，其边长显然就是模型的metric，可以通过圆的相交角计算得出.基于这一方式的度量则称为环包度量.

根据相关理论，环包度量有共形映射的特性，可以将离散形式的映射以任意精度逼近光滑形式的映射.基于这一性质，可以将环包度量从光滑的曲面扩展至离散的三角网格，从而让它适用于基于地理拓扑的无线传感器网络的路由构建.

2.1.3 高斯曲率[7]

当度量给定后，假设曲面中存在一个三角网格N，其顶点分别为a，b，c，令顶点a的内角为∠a，则a的高斯曲率K为

(3)

其中A表示所有包含点a的三角网格，且当点a边界处是Λ的值为π，否则为2π.

根据相关理论，对光滑曲面来说，曲率和曲面拓扑之间关系可以用Gauss-Bonner定理来阐述.同时，高斯曲率由黎曼度量决定.

2.2 曲面Ricci流

早在80年代，美国数学家Hamilton就在其黎曼流形中[10]介绍了曲面Ricci流，并在此后的微分几何发展中，逐渐成为一个热门研究问题.根据曲面Ricci流相关理论，只要预先给定的曲率变换曲面的黎曼度量，就可以将一个几何对象通过变换和扭曲实现曲率的相等.

事实上，曲面Ricci流就是基于给定的曲率进行黎曼度量的过程.假定M是一个平滑曲面，且存在黎曼度量g.令t表示时间参数，用g(t)导入高斯曲率K时，则相应的Ricci流可表示为

(4)

当基于曲面Ricci流的方程开始演变后，其高斯曲率将会变得越来越均匀.当达到最终稳定状态时，即它会流向所需求的目标度量.

3 双曲Ricci流

为获得曲面的双曲拓扑，Chow和Luo等人最先提出了离散Ricci流理论，通过基于metric的参数化方式和简单的实现方法来处理全局范围内的共形化，并将参数作为一个整体.然而，在实际的无线传感器网络环境的部署中，地理环境是不可预定且可能会随着时间的推移而发生改变，同时，传感器的硬件条件限制也可能导致其发生损坏或通信障碍.另外，无线传输协议的选择也在一定程度上影响传输拓扑路径.上述这些情况显然会使得实际传输过程中的拓扑结构图存在诸如空洞等问题.

为此，我们考虑将节点的映射空间变换到双曲空间.基于这一分析，本节首先阐述曲面Ricci流扩展到双曲Ricci流的相关概念.

3.1 离散的黎曼度量

对于一个给定的网格，离散的黎曼度量将方程F

(5)

变成为方程G

G:H→R+

(6)

这意味着，对于该网格中的一个三角面来说，若三条边界长度满足两边之和大于第三边，则对应的夹角满足双曲余弦定理.

3.2 双曲Ricci流

给定一个逆距离环包度量，则双曲Ricci流为

(7)

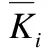
4 基于双曲Ricci流的虚拟坐标构建

对一般传统的Ricci流来说，曲面中包含的三角网格中对应每个顶点夹角必须小于90度.这是因为，当曲面网格中的向量夹角不是锐角时，离散Ricci流会出现不稳定的情形，从而无法得到全局最优解，甚至出现无解的情况.然而，对实际环境下的无线传感器网络来说，所部署的物理空间是不确定的，且传感器本身造成的失效等因素也会导致拓扑关系的改变.换句话说，实际环境下的网络拓扑很难满足这一要求的约束.

为解决这一问题，本文采用了双曲Ricci流进行环包度量[11].在计算度量过程中，我们采用上半盘表示双曲空间.其中，双曲空间的距离的计算方法使用了并使用了交叉比率绝对值的对数的方式.同时，我们选择了合适的莫比乌斯变换.为减少映射过程的能耗，我们进一步基于候选集的思想提出了优化方法，以减少迭代次数.最后，给出相应的虚拟坐标构建算法.

4.1 基于双曲Ricci流的环包度量

根据上文所述，真实环境下的无线传感器网络拓扑中的有可能存在节点的向量夹角大于90度，这将导致该节点无法把信息传递给更靠近目的地的后继节点.因此，在这种情况下，利用贪婪路由策略不能成功地获得合适的路由.为此，文献[11]将传统的环包度量变为双曲空间中的逆距离环包度量，即

lij=cosh-1(coshricoshrj+Iijsinhrisinhrj)

(8)

其中，Iij表示逆距离，ri和rj是两个环的半径.

4.2 双曲空间上半盘模型

(9)

其中，双曲空间的距离的计算方法为交叉比率绝对值的对数.

本文利用的莫比乌斯变换为

(10)

其中，a,b,c,d均为实数，且满足ad-bc=1.

4.3 候选集构建

显然，将整个网络进行坐标映射需要耗费传感器的大量能量.因此，本文考虑将网络拓扑进行分区，然后选择部分传感器作为映射候选集.在区域内采用贪婪算法进行路由构建，区域间的路由构建则从候选集中选择合适的节点.分区的方式根据实际情况的需要进行预先分配.

本文主要关注的是候选集的建立.具体来说，候选集构建过程是：令区域Ci的候选集为Vi，边界为Bi.若va到达Bi的跳数不超过2，则生成一个概率性并基于这一概率将该点并入候选集.其中，概率的选择主要由实际分区内的地理拓扑位置及其具体的通信链路状态决定.一般来说，选择方式有固定和变化两种情形.本文的实验部分将会对比这两种方式的效果.对每个子区域来说，当它们都构建候选集后，将整个网络的候选集合并.显然，该方式充分考虑了边缘节点及其临近节点的在路由构建中的作用，因此使得所构建的路由是全局最优的.换句话说，利用候选集的方式来构建拓扑则避免了将全部网络都进行虚拟映射的过程，从而极大地节约了传感器的能量消耗.

我们将在下一节的实验中将上述优化方式与不使用候选集的方法进行对比.实验结果显示，使用候选集可以有效降低映射过程的能耗.

4.4 构建虚拟坐标的算法

虽然保角变换改变环半径，但却不改变逆距离，因此进行这种变换仅需要计算边界长度.根据这一性质，我们将网络拓扑中所有满足三角不等式形式的节点映射为虚拟坐标，具体算法如下：

算法： 为无线传感器网络节点构建对应的虚拟坐标输入：根据实际部署的物理环境，给定相应的三角网格，其中可能存在空洞现象输出：所有传感器映射的虚拟坐标1． 将整个网络拓扑按照预定要求进行分区2． 对每个区域使用选择概率获得对应的候选集．其中，选择概率根据实际分区中的传感器部署情况决定3． 计算最长边界的长度，并利用传感器通信半径进行约束4． 选择三个节点将之嵌入到平面5． 对于其中的非映射点，检查其邻居平面．若其邻居被映射，则将该平面嵌入曲面．6． 令该映射点到源点的距离在最长边界的长度的1．8～2．1倍之间，令其为上半盘的中心，并将其坐标映射为相应的虚拟坐标．

需要注意的是，在实际应用中，对虚拟坐标的构建要考虑传感器的通信半径，这一点至关重要.另一方面，根据实验验证，映射点到源点的距离并不是固定选取最长边界的长度的两倍，而是应该在一定的范围，原因是随着无线传感器网络中通信要求的改变及其所使用的通信协议，传感器的通信半径会发生相应的调整，从而使得最长边界的长度的约束条件发生改变.因此，不使用固定范围的方式是符合实际情况的.

5 实 验

本节验证了所设计算法的有效性.为更好地检验其性能，我们充分对比了传统Ricci流方法.进一步，我们检测了优化方法的效用.

5.1 对比传统方法

本文首先对比了传统Ricci流方法.在实验中，我们首先将节点分成四组，每组数量分别为10个、30个、50个和90个.它们都是以自组织方式收集一次信息.为保证对比实验的准确性，算法执行100次，然后取结果的平均值.根据实验结果图1所示，本文提出的算法在虚拟映射过程中所需的迭代次数比传统方法少.更重要的是，当网络规模增大时，迭代次数增加非常有限，原因是迭代次数的增加与节点数的增加的比率变化较小.显然，这一优势使得随着网络节点数目的增加，映射能耗需求变化平稳，因此本文方法适用于大规模传感器网络.

无线传感器网络的能量有限特性使得映射过程的迭代次数无法无限制的增加.这意味着即使网络规模不断增加，也要限制其迭代次数.在这种情形下，路由可能无法被有效构建.为此，本文进一步验证路由构建的成功率与迭代次数的关系.我们的实验采用的是90个传感器的网络，且迭代次数分别设为20次、50次、100次和150次.如图 2(b)所示，在相同的迭代次数下，本文算法的成功率较高.因此，该算法可以在迭代次数受限的情况下，尽可能为无线传感器网络成功构建合适的路由.

5.2 评估优化方法

本节评估了所提出的优化方法在不同网络规模下的迭代次数和能量消耗.其中，网络中的传感器个数与上节实验相同.

图3展示了本文优化方法所需的迭代次数与网络规模的关系.其中，优化方法的选择概率分别规定为固定概率和变化概率.根据实验结果，我们的优化方法可以成功构建路由且所需迭代次数小于传统方法，并且当网络规模增大时，能耗节约更大.另外，与上节相似，优化方法所需的迭代次数的增加与节点数的增加的比率增加相对缓慢，因此适合在大规模传感网网络环境下使用. 另一方面，当选择概率变化时，其迭代次

图1 节点数和迭代数的关系Fig.1 Relationship between the number of both nodes and iterations

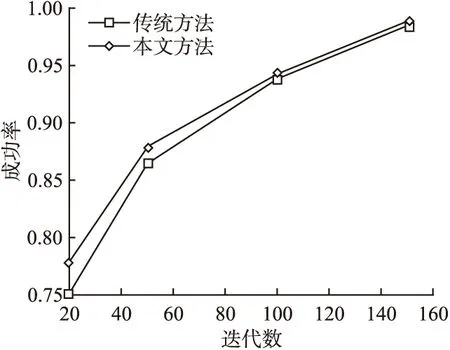
图2 迭代数和成功率的关系Fig.2 Relationship between the number of iterations and the successful rate

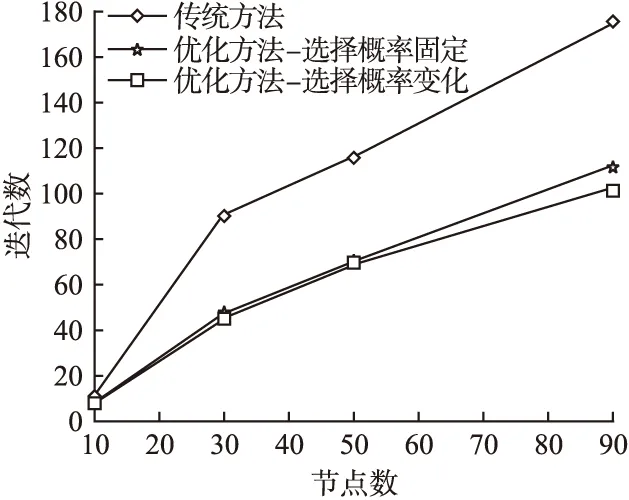
图3 优化方法与传统方法对比Fig.3 Comparison of the optimal schemes and traditional scheme

数总体上少于选择概率固定时的迭代次数，这是因为随着传感器网络的传输，部分节点的链路通信质量发生变化，从而导致网络的拓扑结构发生改变.因此，变化的选择概率更加适应这一情形.从映射结果上来看，优化方法可以达到全局最优.这意味着不选将整个网络中的传感器进行虚拟映射，极大地节约了节点的能耗.

上述实验说明优化方法在保证路由构建正确的前提下，具有明显的能耗优势，可以用于实际无线传感器网络中的路由建立及其数据传输.

6 结 论

为了快速准确地构建合适的无线传感器网络路由，本文提出了一种虚拟坐标构建方法并利用贪婪搜索方式进行路由建立.该方法针对贪婪策略无法解决的空洞问题，利用保角映射方法将网络中的节点映射为相应的虚拟坐标，随后通过直接转发的方式即可得到合适的路由.为降低映射过程能量消耗，本文进一步设计利用候选集来减少不必要的迭代次数.候选集的标准为区域内距离边界不超过两跳的节点.实验验证了本文的方法由于传统的Ricci流方法，且所设计的优化方法也极大地降低了网络能耗，并适用于大规模传感器网络.

[1] Naranjo P G V,Shojafar M,Abraham A,et al.A new s
Table election-based routing algorithm to preserve aliveness and energy in fog-supported wireless sensor networks[J].Proceedings of the IEEE Systems,Man,and Cybernetics,2016:1-6.

[2] Sharma A,Agrawal M,Sondhi M,et al.Analysis and simulation of energy efficient optimal scenarios for cluster based routing protocol in wireless sensor network[J].Journal of Network Security Computer Networks,2016,2(1):79-86.

[3] Rahat A A M,Everson R M,Fieldsend J E.Evolutionary multi-path routing for network lifetime and robustness in wireless sensor networks[J].Ad Hoc Networks,2016,52:130-145.

[4] Liu J,Wan J,Wang Q,et al.A survey on position-based routing for vehicular ad hoc networks[J].Telecommunication Systems,2016,62(1):15-30.

[5] de Oliveira H A B F,Boukerche A,Guidoni D L,et al.An enhanced location-free greedy forward algorithm with hole bypass capability in wireless sensor networks[J].Journal of Parallel and Distributed Computing,2015,77:1-10.

[6] Das D,Misra R,Raj A.Approximating geographic routing using coverage tree heuristics for wireless network[J].Wireless Networks,2015,21(4):1109-1118.

[7] Tromba A.Teichmüller theory in riemannian geometry[M].Birkhäuser,2012.

[8] Stephenson K.Introduction to circle packing:The theory of discrete analytic functions[M].Cambridge University Press,2005.

[9] Thurston W P,Milnor J W.The geometry and topology of three-manifolds[M].Princeton:Princeton University,1979.

[10] Hamilton R S.The Ricci flow on surfaces[J].Contemporary Mathematics,1988,71(1):237-261.

[11] Yang Y L, Guo R, Luo F,et al. Generalized discrete Ricci flow[J]. Comput. Graph. Forum, 2009,28(7): 2005-2014.

[12] Chow B, Luo F. Combinatorial ricci flows on surfaces[J]. Communications in Contemporary Mathematics, 2012, 63(1):765-780.

[13] Terras A. The poincaré upper half-plane[M]. Springer New York, 2013.