微积分思想方法及教学思考

舒斯会 易云辉

摘 要：微积分思想方法是微积分的基础和精髓。在教学过程中，应尽早地让学生接触和了解微积分思想方法。文章总结了微积分思想方法的三个步骤，并介绍了在微积分教学中，怎样引入和应用微积分思想方法，为读者讲授微积分思想方法提供参考。

关键词：微积分；微积分思想；教学思考

中图分类号：O172

文献标识码：A

微积分思想方法是微积分的基础和精髓，是微积分创立和发展的基石，所以学好微积分的关键是要理解和掌握好微积分思想与方法。所以在教学过程中，要尽早地让学生接触和了解微积分思想方法。建议在讲完数列极限后，就对微积分思想方法进行较为系统的介绍。

微积分思想方法来源于现实并能广泛应用于现实，特别是平面图形面积、曲线的切线和非匀速运动物体的瞬时速度计算等问题在微积分的建立过程中起到极其重要的作用，毫不夸张地说微积分就是当初为了解决这些方面的问题而产生的。在教学过程中，我们可以通过微积分的上述几个方面经典应用来引出微积分思想方法，这样能帮助学生了解微積分思想方法产生的过程及其应用。下面是我们在微积分思想方法的过程。

一、微积分思想方法的引入

我们通过观察以下现象导出微积分思想方法并对微积分思想方法进行了系统的总结，使学生对微积分思想方法有完整系统的认识。

（1）引入：如图1，设L是一条连续曲线，在曲线上任取很小的一曲线段A1A2，发现它很接近直线段。而且不难理解曲线段分（取）的越细，它越接近直线段。

我们可以将任意的曲线段进行不断的细分，如不断用曲线段的中点对它们进行不断的细分，使得每个细分的曲线段的长度无限接近零，那么这些曲线段也就无限接近直线段。

根据上述发现，数学家创立了一种先对曲线段无限细分，再用直线来近似代替细分后的每曲线段（即以直代曲），然后取极限（看无穷趋势）的数学方法。由此，归纳出下列微积分思想方法。

（2）微积分思想方法：第一步无限细分；第二步近似（以直代曲）；第三步取极限。

这三个步骤缺一不可，近似是微积分方法的精髓，它主要包括用直线来近似代替曲线（简称以直代曲）和以不变的量来近似代替变化的量（简称以不变代变）。 无限细分是近似的前提，没有无限细分，近似不可能通过无限接近（求极限）达到准确。第三步需要通过看近似的极限得到准确，也是我们要求的结果。

这样让学生在开始学习微积分时就对微积分思想方法有一个系统的认识，明白微积分思想方法包含三个步骤，不能片面的理解微积分思想方法只是“以直代曲”或 “以不变代变”。

紧接着我们讲述微积分思想方法在曲边图形的面积、曲线的切线计算等问题的应用，让学生知道微积分思想方法的强大作用，提高学生学习微积分的兴趣。

二、微积分思想方法的应用

在讲微积分思想方法应用时，要紧扣其三个步骤。

1.曲边图形的面积

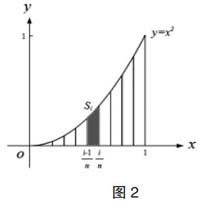
例1，求由曲线y=x²， 0≤x≤1，和直线x=0，x=1，y=0所围曲边梯形的面积S。

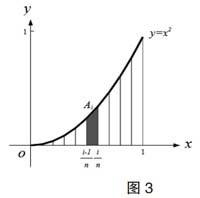
解：（1）无限细分，即将x轴的区间[0，1]细分成n等分，然后过各分点作平行y轴的直线与曲线y=x²相交，这样将曲边梯形分成n个小曲边梯形S_i，其面积仍记为 S_i（如图2）；