利用多步流动试验预估非饱和土平衡时间的理论研究

陈辉，陈芳芳，郭敬林

（江西科技学院，江西南昌 330098）

0 引言

非饱和土土水特征曲线反映了非饱和土基质吸力与体积含水率（或饱和度）等能描述含水率的物理量之间的关系。利用它可以研究非饱和土的抗剪强度、边坡稳定、污染物的迁移等问题[1-5]。因此，非饱和土土水特征曲线在非饱和土的科学研究及工程实践中起着重要的作用。

传统测量非饱和土土水特征曲线的方8/z法主要采用直接法进行测试，然而该测试技术要求试样达到平衡状态。一般试验人员预判试样达到平衡状态主要是通过延长测试试验点的时间进行。众所周知，延长测试试验点的时间意味着增加了高压气体析出的几率，从而影响试验测试的精度。因此，如何准确预测非饱和土在某一基质吸力作用下达到平衡状态的时间提高试验测试的精度，就显得尤为重要。本文通过研究基质吸力和饱和度之间的增量关系，结合多步流动试验的边界条件，探索多步流动试验溢出量的演化规律，进而得到确定非饱和土平衡时间的理论模型。

1 土水特征曲线动态模型

2006 年，韦昌富&Dewoolkar[6]在多相多孔介质非平衡渗流理论的基础上，提出了不考虑土骨架变形的非饱和土气-水两相流模型，其表达式为

非饱和土在平衡状态时，基质吸力增量与饱和度增量存在如式（2）所示的关系式。

依据体积含水率与饱和土的关系，可得到其相应的增量表达式，其表达式如式（3）所示。

将式（2）、（3）代入到（1）可以得到非平衡状态下基质吸力增量与饱和度增量之间的关系式，即非饱和土非平衡态土水特征关系，其表达式如式（4）所示。

在MM定理之后，突破原先的理想条件，有学者基于非对称信息提出了代理理论、权衡理论等。权衡理论认为，虽然在一定程度内负债增加可以产生税盾效应，但是过多的负债也会对公司造成巨大的还款压力，企业破产风险上升，即财务困境成本增加。2004年我国学者曹延求、孙文祥在代理成本的背景下，通过实证分析发现，资本结构中债务融资的比例增加会导致公司业绩下降。

2 多步流动试验溢出量演化方程

从式（4）的表达式可以看出，该方程是一个一阶非齐次线性微分方程，其通解为

图1 多步流动试验

当开展如图1所示的多步流动试验，其施加过程如下所述：

在初始时刻t1之前，试样在基质吸力pc0的作用下处于平衡状态。随后，将基质吸力突然增加一个小的增量Δpc1，此时试样的基质吸力变为pc1=pc0+Δpc1，并保持该基质吸力不变至t2时刻；然后，在t2时刻，将基质吸力再增加一个小的增量Δpc2，此时基质吸力变为pc2=pc0+Δpc1+Δpc2，并保持该基质吸力不变至 t3时刻；……；一直到时刻tn，此时的基质吸力突然增加Δpcn，使得基质吸力变为pcn=pc0+∑Δpci，然后保持该基质吸力不变。

施加如上所述的边界条件，可以通过式（5）得到饱和度变化关系式，其表达式如式（6）所示。

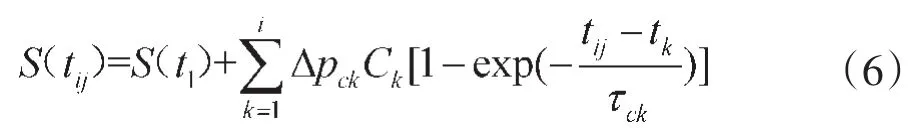
众所周知，饱和土与溢出量之间存在如式（7）所示的关系。

根据饱和度与溢出量之间的关系式，式（6）的饱和度变化关系式可以转变为溢出量变化关系式，其表达式如式（8）所示。

3 平衡时间的确定

在实际工程实践中，以相邻两时刻的溢出量不超过某一允许误差，即认为其达到了平衡。因此有

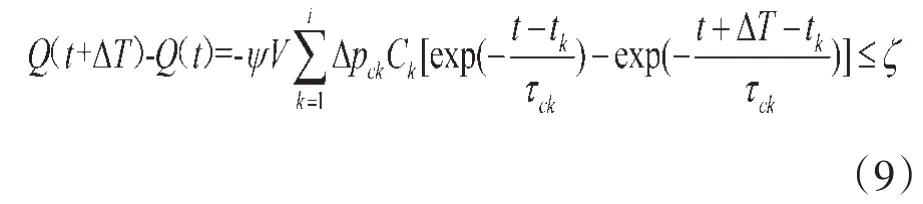
对式（9）进行泰勒展开，则有

4 结论

本文仅仅围绕非饱和土平衡时间的确定这一研究热点开展相关的理论研究，并得出以下结论：

4.1 基于韦昌富&Dewoolkar不考虑孔隙体积变化的非饱和土气-水两相流流动模型，通过引入平衡状态下非饱和土土水特征曲线的容水率这一变量，在每级基质吸力作用下的溢出量数据中选取两个数据点，通过采用式（8）进行模拟可以求得相对应的容水率和平均特征时间。将求得的数值代入式（10）并采用数值迭代的方式可以求平衡时间。建立非饱和土基质吸力与饱和度间的增量模型，用于描述非饱和土土水特征关系的动态变化。

4.2 针对非饱和土土水特征曲线测试的过程，并结合其施加的边界条件，得到非饱和土溢出量随时间的变化规律。

4.3 通过给定试样达到平衡的标准，结合溢出量随时间变化的规律，采用数值反演的方式，得到试样达到平衡时所需的时间。

[1]李万双,孙德安,高游.土水特征曲线预测非饱和黏土的抗剪强度[J].上海大学学报（自然科学版）,2016,22(5):648-655.

[2]王晨沣,张守红,王彬,王玉杰,王云琦,胡波,王凯.不同土壤前期含水量对土壤分离临界水动力学特性及其抗剪强度的影响[J].水土保持学报,2017,31(1):91-96.

[3]郭利娜,胡斌,宋友建,张国超.土-水特征曲线预测非饱和土的抗剪强度对比研究[J].工程地质学报,2013,21(6):849-856.

[4]朱伟,舒实,王升位,徐浩青,范惜辉.垃圾填埋场渗沥液击穿防渗系统的指示污染物研究[J].岩土工程学报,2016,38(4):619-626.

[5]唐栋,李典庆,周创兵,方国光.考虑前期降雨过程的边坡稳定性分析[J].岩土力学,2013(11):3239-3248.

[6]WEI C F,DEWOOLKAR M M.A continuum theory of non⁃equilibrium two-phase flow through porous media with capil⁃lary relaxation[C]//Advances in Unsaturated Soil,Seepage,and EnvironmentalGeotechnics,ProceedingsofSessionsof GeoShanghai.Shanghai:GeotechnicalSpecialPublications,2006:246-254.