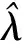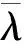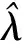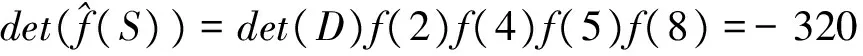Determinants of Generalized GCD Matrices Associated with Arithmetic Functions

ZHU Yuqing, LIAN Dongyan, DIAO Tianbo, HU Shuangnian,2

( 1. College of Mathematics and Statistics, Nanyang Institute of Technology, Nanyang 473004, Henan;2. College of Mathematics and Statistics, Zhengzhou University, Zhengzhou 450001, Henan)

1 Introduction and statements of main results

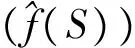
Throughout this section, we letfbe an arithmetic function andS={x1,x2,…,xn} be a set ofndistinct positive integers. We can now give the first two main results of this paper, which extend Bege’s results[20].

Then each of the following is true:

and then×nmatrixD=(dij) is defined by

In what follows, we always let then×nmatricesCandDbe defined as in Theorem 1.1.From Theorem 1.1, one can deduce the following result of Bege[20].

Then each of the following is true:

FromTheorem1.2,onecandeducethefollowingresultofBege[20].

From Theorems 1.1 and 1.2, we can easily get the following result.

We organize this paper as follows. In Section 2, we prove Theorems 1.1 and 1.2. In Section 3, some examples are given to illustrate our main results.

2 Proof of Theorems 1.1 and 1.2

In this section, we prove Theorems 1.1-1.2. We begin with the proof of Theorem 1.1.

ProofofTheorem1.1(i) Write

A=Cdiag(f(x1),f(x2),…,f(xn))DT.

Then for any integersiandj(1≤i,j≤n), we have

Thus,

So the desired result follows immediately. This completes the proof of part (i).

det(C)det(diag(f(x1),f(x2),…,f(xn)))×

(iii) As the argument given in part (ii), we let 1≤x1

This ends the proof of Theorem 1.1.

ProofofTheorem1.2(i) For any integersiandjwith 1≤i,j≤n, we have

So the desired result follows immediately. This completes the proof of part (i).

(ii) Using part (i), one infers that

det(D)det(diag(f(x1),f(x2),…,f(xn)))×

Since Corollaries 1.1～1.3 are very easy to get, we omit their proofs here.

3 Examples

In this section, we give some examples to demonstrate our main results.

Example3.1LetS={2,4,8,12,16} andλbe the Liouville function which is defined by

Then one has

By Theorems 1.1 and 1.2, we have

and

Furthermore, we have

Example3.2LetS={2,4,5,8}. For any positive integern, we letf(n)=n. Then we obtain

From Theorems 1.1 and 1.2, we have

and

Moreover, we have

and

AcknowledgementsThe authors would like to thank the anonymous referee for careful reading of the manuscript and helpful comments that improve the presentation of this paper.

[1] SMITH H J S. On the value of a certain arithmetical determinant[J]. Proc London Math Soc,1875,7(1):208-212.

[2] BESLIN S, LIGH S. Another generalization of Smith’s determinant[J]. Bull Aust Math Soc,1989,40(3):413-415.

[3] BOURQUE K, LIGH S. Matrices associated with classes of arithmetical functions[J]. J Number Theory,1993,45(3):367-376.

[4] BOURQUE K, LIGH S. Matrices associated with arithmetical functions[J]. Linear Multilinear Algebra,1993,34(3/4):261-267.

[5] BOURQUE K, LIGH S. Matrices associated with multiplicative functions[J]. Linear Algebra Appl,1995,216(2):267-275.

[6] CODECA P, NAIR M. Calculating a determinant associated with multiplicative functions[J]. Boll Unione Mat Ital Sez B:Artic Ric Mat,2002,5(2):545-555.

[7] HILBERDINK T. Determinants of multiplicative Toeplitz matrices[J]. Acta Arith,2006,125(3):265-284.

[8] HONG S. Gcd-closed sets and determinants of matrices associated with arithmetical functions[J]. Acta Arith,2002,101(4):321-332.

[9] HONG S. Factorization of matrices associated with classes of arithmetical functions[J]. J Algebra,2003,281(1):1-14.

[10] HONG S. Nonsingularity of matrices associated with classes of arithmetical functions[J]. Linear Algebra & Its Applications,2006,416(1):124-134.

[11] HONG S, LI M, WANG B. Hyperdeterminants associated with multiple even functions[J]. Ramanujan J,2014,34(2):265-281.

[12] HONG S, LOEWY R. Asymptotic behavior of the smallest eigenvalue of matrices associated with completely even functions (modr)[J]. Int J Number Theory,2011,7:1681-1704.

[13] 胡双年,陈龙,谭千蓉. 定义在两个拟互素因子链上与算术函数相关联矩阵的行列式[J]. 四川大学学报(自然科学版),2015,52(1):6-10.

[14] HU S, HONG S. Multiple divisor chains and determinants of matrices associated with completely even functions (modr)[J]. Linear Multilinear Algebra,2014,62(9):1240-1257.

[15] HU S, HONG S, ZHAO J. Determinants of matrices associated with arithmetic functions on finitely many quasi-coprime divisor chains[J]. Appl Math Comput,2015,258(1):502-508.

[16] 胡双年,谭千蓉,赵相瑜.k-集合上与算术函数关联矩阵的行列式[J]. 四川大学学报(自然科学版),2015,52(3):456-460.

[17] TAN Q. Divisibility among power GCD matrices and among power LCM matrices on two coprime divisor chains[J]. Linear Multilinear Algebra Appl,2013,438(3):1454-1466.

[18] 赵建容. 使得幂GCD阵(Se)整除幂LCM矩阵[Se]的四元gcd封闭集S的一个刻画[J]. 四川大学学报(自然科学版),2008,45(3):485-487.

[19] 赵建容,赵伟,李懋. 六元gcd 封闭集上Smith 矩阵的整除性[J]. 数学学报,2011,54(4):609-618.

[20] BEGE A. Generalized GCD matrices[J]. Acta Univ Sapientiae Math,2010,2(2):160-167.

[21] TAN Q. Divisibility among power GCD matrices and among power LCM matrices on two coprime divisor chains[J]. Linear Multilinear Algebra,2013,438(3):1454-1466.

[22] WAN J, HU S, TAN Q. New results on nonsingular power LCM matrices[J]. Electronic Journal of Linear Algebra,2014,27(1):652-669.

[23] HONG S, HU S, LIN Z. On a certain arithmetical determinant[J]. Acta Math Hungar,2016,150(2):372-382.

[24] HONG S, HU S, HONG S. Multiple gcd-closed sets and determinants of matrices associated with arithmetic functions[J]. Open Math,2016,14(1):146-155.

[25] HU S, LIAN D, DIAO T, et al. Further results on generalized LCM matrices[J]. 武汉大学学报(自然科学英文版),2017,22(1):1-4.