计算全马赫数流场的温度和压力基本变量方法

柳 建, 李树民, 金 钢

(1. 成都理工大学 工程技术学院， 四川 乐山 614007；2. 中国空气动力研究与发展中心， 四川 绵阳 621000)

完全可压缩流和不可压缩流在计算流体力学中有比较完整的研究和应用[1-4].近20年来,出现了许多对高低速流采用统一格式求解的研究[5-6]，这种求解方式通常采用条件预处理或者通量限制器组合的方法.近年来,对低速流的计算方法研究主要集中在条件预处理和守恒变量方法上[7-8]，但对流体的可压缩性研究较少.总的来说，对于弱可压缩流的研究相对较少.通常在弱可压缩流的计算中采用Bossinesq假设或摄动法，这样一来对低速流体密度变化的捕捉十分困难，而在一些计算中密度变化量又是很重要的量[9-11]，因而需要研究求解低速弱可压缩流密度变化的方法.Wesseling等[12]对低马赫数下的弱可压缩流体的计算进行了探讨.基于他们的方法，采用全场音速为归一化因子的压力原变量方法，以消除在流马赫数趋于零时由于归一化引起的压力项奇性和右端源项消失的困难.对这种方法做出完整的推导并给出离散形式，并用几个算例进行数值计算.计算结果显示该方法能够较好地统一处理从零马赫数到较高马赫数的流场计算问题，尤其是能较好处理弱可压缩流问题.

1 压力原变量控制方程

基于压力原变量的全马赫数流模型的控制方程，可从Euler方程组得到.一维Euler方程组的守恒形式[1-2]为

Ut+∂f(U)/∂x=Q，

(1)

首先,从(1)式中消去内能项，把能量方程表示为温度的形式.利用理想气体状态方程

(2)

其中,e为内能，γ为比热容.把连续方程代入能量方程中，就可以得到能量方程的温度T表示形式

(3)

继而利用密度、温度和压力的关系得出压力的控制方程.由状态方程，可以把密度写成下面的形式

ρ=ρPP+ρTT，

(4)

代入连续方程得到压力的控制方程

ρPPt+ρPTt+mx=0,

(5)

其中，ρP=1/(RT)，ρT=-ρ/T.

由于密度是压力和温度的函数，只要得到温度和压力的空间分布值就可以利用状态方程

ρ=P/(RT)

(6)

求出密度.

上面的推导中动量方程保持不变，仍然写作

mt+(um+P)x=ρfb,

(7)

其中,速度可以通过其与密度和动量的关系得到.到此，(3)、(5)、(6)和(7)式构成以温度、压力和动量为基本变量的封闭方程组.

2 压力原变量方程组的离散和求解

下面给出压力原变量方程组的离散求解过程.为避免出现压力项的锯齿波问题，因而采用交错网格[3-4].为表述简便起见，尽量略去一些无关紧要项.令λ为时间步长与空间步长的比值，对(3)式略去外力项做功后离散得

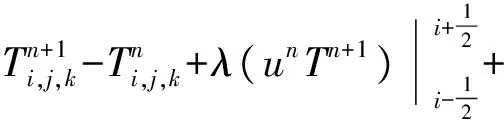
(8)

对(5)式离散得

(9)

对(7)式离散得

(10)

计算中，当变量的取值位置与网格预定变量位置不相同时,使用vanAlbada通量限制器进行插值

其中

(11)

为得到更高的时间精度和稳定性，使用四阶龙格-库塔法分步求解(8)和(10)式.为简化计算，假设

且

(12)

用Pn代替(10)式中的Pn+1，然后用四阶龙格-库塔法对(8)和(10)式联立求解得到Tn+1和m*.

把(12)式代入(9)式得到如下关于δP的方程

α1δPj-1+α2δPj+α3δPj+1=Fp.

(13)

这是一个三对角方程组，可以通过高斯-赛德尔迭代法求解.最后把δP代入(12)式得到mn+1.

3 算例结果及分析

采用压力原变量方法，对Sod[13]提出的激波管问题和Arora等[14]提出的马赫3问题进行了计算，初始条件为：

Sod激波管问题case1：t=0,u1=0，P1=1，ρ1=1，u4=0，P4=0.1，ρ4=0.125；

马赫3问题case2：t=0,u1=0.92，P1=10.333，ρ1=3.857，u4=0，P4=1，ρ4=1.

以上问题中的时间、压力、密度都为无量纲的归一化单位.将计算值和理论值进行比较，分别得到图1和图2的结果.

图 1 Sod激波管算例计算结果

图 2 马赫3算例计算结果

图1是case 1在t=0.15时的结果，图2是case 2在t=0.087 5时的结果，实线是理论值，离散点是计算值.从图中可以明显看出，计算值与理论值的间断位置符合较好，误差小于3%，间断两侧的密度符合也较好，普遍小于10%;但在小几何区间的连续间断点处，符合不太好，密度误差达到5%，在个别间断点超过10%.考虑到其他以密度为原变量的守恒方法的计算结果与理论解也存在较大的误差，因而仍然可以认为本方法具有较好的符合度.

对低速弱可压流，计算了封闭方腔中的微加热例子.初始条件为：ρ=1.226kg/m3,T=300K,q=[47 015·exp(-r2/0.036)]2·α,R=297,P=ρRT,v=0m/s，其中，ρ是密度，T是温度，P是压强，R是气体常数，v是速度，q是方腔内中心对称呈高斯分布的热源，α=6.5×10-5/m是气体吸收系数.方腔的边长是 0.6m，g=9.8m/s2是重力加速度.图3和图4给出了在t=0.5 s时的腔内密度等值线分布和流线情况.

图 3 在t=0.5 s时的密度等值线分布

图 4 在t=0.5 s时的流线图

在强光控制中，有时为抑制热晕效应，会采用吹入或充入惰性气体的方式[15].其中，在吹气速度较大时，流场密度也会变得不均匀，属于典型的弱可压缩问题.对这样的情况也采用压力原变量方法进行了计算，表1给出了5、10、20和30 m/s吹气速度下流场密度的最大、最小值和均方根值(采用初始密度进行了归一化),图5给出了3种吹速下的密度分布云图.

表 1 各种吹速下流场内密度参数值

图 5 吹气速度为5、10、30 m/s时的流场密度云图

从以上2个完全可压缩流和2个低速弱可压缩流算例的计算结果可以看出，压力原变量方法能够较好地解出激波层的密度、压力和速度分布，尽管在激变处与理论值还有一定的偏差，但考虑到模型方程在求解过程中仅使用了二阶中心差分格式，并且没有计入扩散项和湍流脉动，这个结果还是可以接受的；而在处理低速弱可压缩问题上，可以获得细微的密度变化和流速变化，十分利于求解一些关注流场密度分布的问题[16].由此可见，该方法可作为一种统一的处理方法来处理工程计算中的强弱压缩流问题.

4 结论

从守恒格式的Euler方程组推导出了基于压力原变量的流体控制方程.通过在交错网格上离散，给出了该方程的完整离散格式和数值求解过程，并通过4个算例验证了其可以很好地应用于可压缩流和弱可压缩流的计算.求解过程简单，易于推广到热、流耦合计算中去.

[1] 朱自强,吴子牛,李津,等. 应用计算流体力学[M]. 北京：北京航空航天大学出版社，1998：1-20.

[2] 张君. 基于笛卡尔网格的预处理方法及应用研究[D]. 南京：南京航天航空大学,2016.

[3] 陶文铨. 数值传热学[M]. 2版. 西安：西安交通大学出版社,2001:1-26.

[4] PATANKAR S V. Numerical Heat Transfer and Fluid Flow[M]. New York:McGraw-Hill,1980:1-31.

[5] 李雪松,顾春伟,徐建中. 新型高低速流统一算法及其叶轮机应用[J]. 航空学报,2007,28(6):1334-1338.

[6] 李国良,尚庆,袁湘江. 基于全局预处理方法的全马赫数算法研究[C]//第2届空间工程及信息技术国际国际会议(AEIT 2012). HongKong:Hong Kong Education Societ，2012：128-135.

[7] 白晓征,郭正,刘君. 粘性极低速流动的预处理方法研究[J]. 空气动力学学报,2009,27(4):451-455.

[8] 韦安阳,樊建人,罗坤,等. 低马赫数方法在自然对流数值模拟的应用[J]. 工程热物理学报,2011,32(9):1549-1552.

[9] LIU J, WANG S Q. Weakly compressible fluid model to study thermal effects on laser propagating in closed tube[J]. Applied Materials Research,2012,1478(354):165-169.

[10] 王世庆,柳建,张翔,等. 光路交叠对强光传输的影响[J]. 光子学报，2008,37(1):173-176.

[11] 柳建,金钢,王世庆,等. 研究连续激光内通道传输的弱可压缩流模型[J]. 强激光与粒子束，2006,18(12):1983-1986.

[12] WESSELING P. Principles of Computational Fluid Dynamics[M]. Berlin：Springer-Verlag,2000:578-601.

[13] SOD G A. A survey of several finite difference methods for systems of nonlinear conservation laws[J]. J Comput Phys,1978,27(1):1-31.

[14] ARORA M, ROE P L. A well-behaved TVD limiter for high-resolution calculations of unsteady flow[J]. J Comput Phys,1997,132(1):3-11.

[15] 柳建,李树民,赵杰,等. 镜面热变形及吹气流场对光束的联合影响[J]. 光学精密工程，2014,22(8):56-62.

[16] 柳建. 近封闭环境下激光传输特性仿真分析平台研究[D]. 北京：中国科学院研究生院，2005.