一种基于SGCMG的欠驱动姿态控制方法

刘美师,吴敬玉,王文妍,杨盛庆,谢任远

(上海航天控制技术研究所，上海 201109)

0 引言

随着卫星趋于大型化发展，控制力矩陀螺(CMG)因其具有输出力矩大、控制效率高等优点常被选为执行机构。若卫星的控制系统中只剩两个单框架控制力矩陀螺(SGCMG)可以使用，则控制系统输入维数少于输出维数，称为欠驱动姿态控制[1]。欠驱动卫星的姿态控制系统处于一种非完整配置状态，是一种不可积分约束的非线性系统[2]。欠驱动姿态控制可以在卫星的部分执行机构失效时维持基本姿态，还能减轻整个控制系统的功耗、质量、体积。传统的线性控制方法及现代控制理论不能直接应用于欠驱动卫星的姿态控制问题。

欠驱动控制主要有四类，分别为间断反馈控制、时变稳定控制、混合控制、最优控制。反馈控制通过进行非奇异坐标变换来解决非线性问题，主要应用于原系统可以实现状态反馈的情况；时变稳定控制法通过参数在一定范围内变化来实现控制系统的收敛，应用于系统参数实时可测的情况；混合控制法结合多种线性控制，通过控制器的切换来实现对稳健性要求不高的系统的控制；最优控制法通过构建一个特定的性能指标，对这个指标求极值来求解控制器，主要应用于非线性较弱的系统[3-7]。而欠驱动卫星姿态稳定控制主要有两大类，即间断定系数状态反馈控制和连续时变状态反馈控制[8-9]。国内外对CMG的研究主要针对CMG的奇异问题，集中在操纵律设计上[10-13]。关于欠驱动卫星最早的理论研究可以追溯到1984年，Crouch等基于微分几何理论分别针对刚体卫星在有一、二、三个独立控制输入力矩的情况下，给出了卫星能控的充要条件[14]。并证明如果欠驱动卫星是非轴对称的，则卫星在平衡点都是局部能控的。对于欠驱动卫星要实现其在两个给定姿态之间进行机动，通常有两种方式：基于最优控制策略的轨迹规划算法或基于卫星特殊特性(微分平滑、微分包含等)的轨迹规划算法[15]。

针对欠驱动卫星的姿态控制问题，在失控轴方向上无对应的执行机构提供控制力矩，只能通过其余两轴上执行机构的耦合影响来实现控制，因此较难处理的就是失控轴角速度分量对卫星姿态的影响。SGCMG只能提供单自由度的控制力矩，通常构成一定构型如五棱锥构型、金字塔构型、双平行构型等。前人对SGCMG的研究集中在组成特定构型后如何避免奇异问题，而未考虑只剩两个SGCMG可用的欠驱动控制情况。戈新生[16]以两个飞轮为执行机构，并在整星零动量条件下通过最优控制方法和Ritz近似理论，得到以两个动量飞轮为执行机构的欠驱动控制律。SGCMG较飞轮有更强的控制力矩输出能力，能实现对更恶劣工况的控制，但需要增加操纵律设计来解决SGCMG带来的奇异问题。本文通过欠驱动卫星姿态稳定控制律和SGCMG操纵律的设计，实现了使用SGCMG的欠驱动控制。其中控制律决定如何用两维控制力矩控制三轴姿态，操纵律决定如何用两个SGCMG提供两维控制力矩。

1 数学模型的建立

假设研究对象为刚体卫星，由欧拉方程导出姿态动力学方程，并建立用四元数描述的姿态运动学方程。

1.1 卫星姿态动力学模型

定义卫星本体坐标系的三个轴，分别沿其主惯量轴方向。刚体卫星旋转运动方程为

(1)

(2)

定义中间变量

(3)

则动力学方程可以简化为

(4)

式(4)为z轴欠驱动时卫星的姿态动力学模型，其中u1和u2为控制器的输入变量，c3为常数。

1.2 卫星姿态动力学模型

设q是把参考系转动到星体系时对应的转动四元数，则卫星运动学方程为

(5)

四元数运动学方程不涉及三角函数，无奇点，且满足归一化约束条件。

2 控制器设计

根据系统动力学和运动学方程，首先设计一个能实现姿态动力学系统稳定的控制律，将卫星的角速度控制为零，使失控轴的角速度不会对姿态角产生影响；然后在失控轴的角速度分量已经收敛到零后，采用反步法对姿态角控制律进行设计；最后由SGCMG力矩方程导出两个SGCMG的操纵律。结合姿态稳定控制律和SGCMG操纵律，能够实现欠驱动卫星姿态稳定控制。

2.1 角速度控制律

为了剥离ωx和ωy对ωz的耦合影响，对动力学方程(4)中的第三式求导,可得到失控轴角速度分量的二阶导数

(6)

(7)

结合式(4)、(6)、(7)求出控制律形式如下

(8)

式中：k1d，k1p为控制器参数；ε为一个用于避免奇异的小参数。

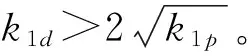
2.2 姿态角控制律

反步法的核心在于设计合适的中间控制律，控制系统实现三轴角速度的稳定后，反步法设计出的控制器只需实现四元数的收敛，这个控制器作用过程中角速度的变化直接决定四元数的变化，因此要设计一个合适的角速度中间控制律。

假设在角速度中间控制律的作用下姿态四元数q1、q2的目标收敛形式为

(9)

代入姿态运动学方程(5)中可解得角速度中间控制律为

式中：k>0为控制器参数；E2和H为参数矩阵

(11)

欠驱动轴角速度ωz是一个接近于零的小量，对式(9)进行修正，并引入耦合参数β，有

(12)

则角速度中间控制律式(10)调整为

由式(12)可知在ωz为小量的前提下，如果β收敛到零，则q1和q2收敛到零。令q3的收敛形式为

(14)

q3的收敛通过调节参数β的大小来实现。结合运动学方程(5)、角速度中间控制律式(13)和q3收敛形式式(14)可以求出包含耦合项的参数

(15)

式中：k3>0为反步法控制器的参数；e2>0是一个充分小的正数，可以使控制参数不会进入奇异。参数β跟随ωz的变化进行收敛，q3也收敛。选择合适的参数，可以使q3迅速收敛。在角速度跟踪误差消除之后，卫星的角速度能跟随所设计的角速度中间控制律的变化而变化。参数β保持单调变化，且最终收敛到零。

2.3 SGCMG操纵律

SGCMG操纵律是指根据控制器产生的指令力矩，解算出相应的框架转动指令，驱动电机使各个SGCMG的框架轴转动，使得SGCMGs的总角动量发生改变，从而提供需要的控制力矩。理想情况下操纵律可以使SGCMGs的输出力矩和控制器产生的指令要求的控制力矩大小相等。

(16)

式中hw为单个SGCMG角动量大小。对式(16)两端进行求导，得

(17)

(18)

由式(18)可得操纵律，即SGCMGs的框架角速度为

(19)

3 仿真结果与分析

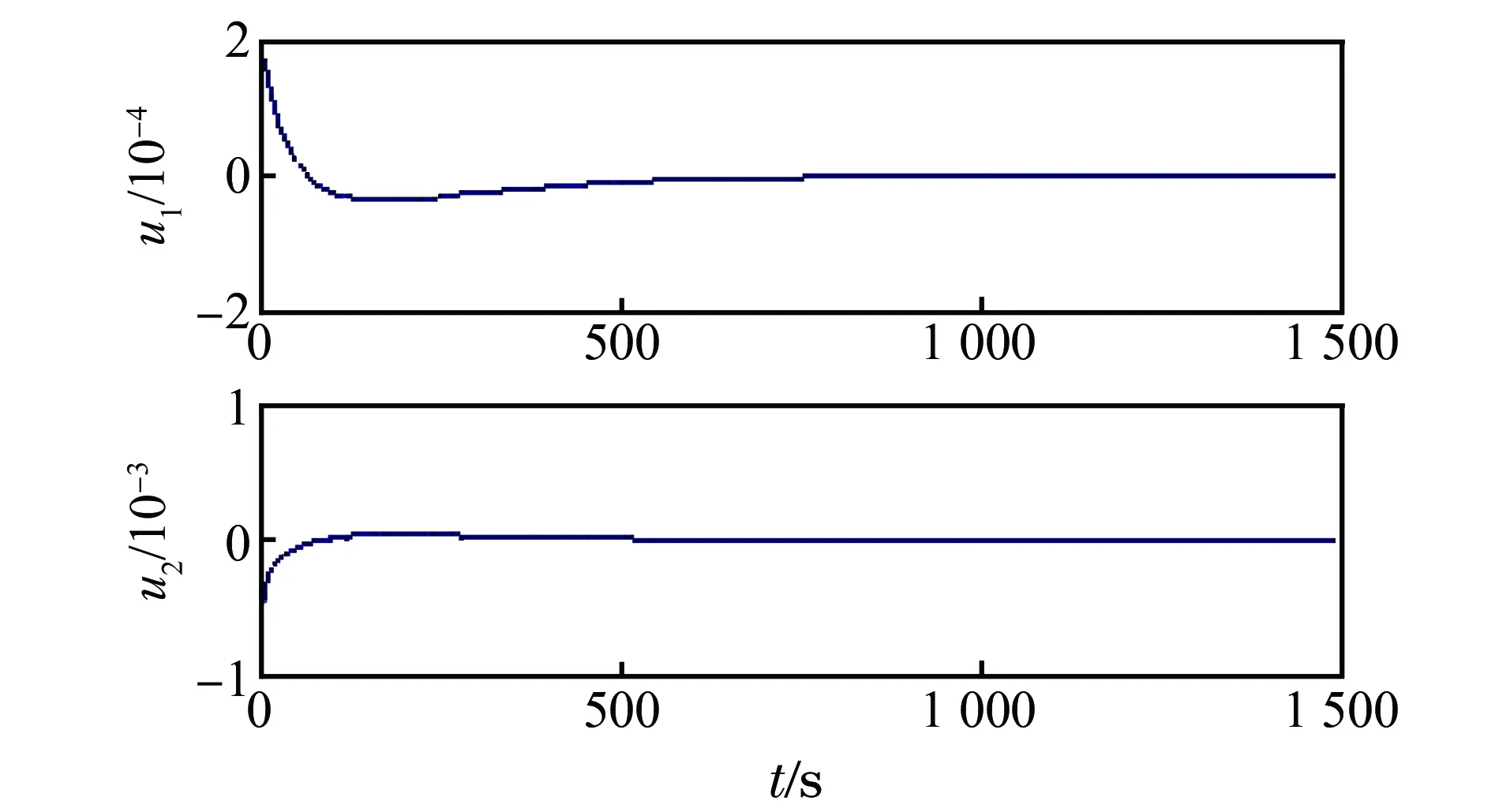
图1 控制器输入Fig.1 Input of the controller

图2 控制力矩Fig.2 Controlling torque

从图1、图2可以看出，控制量和控制力矩都是一个小量。从图3可以看出，SGCMG框架角速度和转动的框架角也保持在初值的一个小的邻域内。从图4可以看出，在状态反馈非线性控制器的作用下，在仿真时间780 s后欠驱动卫星角速度收敛到零。

图3 SGCMG框架角速度Fig.3 Angular velocity of the SGCMG

图4 星体角速度Fig.4 Angular velocity of the satellite

图5 反步控制器作用下的控制力矩Fig.5 Controlling torque under with the back-stepping controller

图6 反步控制器作用下的角速度中间控制律Fig.6 Angular velocity controlling law with the back-stepping controller

图7 反步控制器作用下的姿态四元数Fig.7 Attitude quaternion with the back-stepping controller

图8 反步控制器作用下的SGCMG框架角速度Fig.8 Angular velocity of the SGCMG with the back-stepping controller

4 结束语

针对基于SGCMGs的欠驱动卫星，首先建立刚体卫星姿态控制系统的数学模型；根据动力学方程设计状态反馈控制器；根据运动学方程设计反步法控制器；再结合SGCMGs的操纵律实现欠驱动姿态控制。所提出的结合反步法控制器和SGCMGs操纵律的方法避免了使用SGCMGs控制过程中的奇异问题，实现欠驱动卫星的姿态稳定控制。本文设计的角速度中间控制律要求先将失控轴的角速度控制到零后再进行下一步控制，对控制过程中的误差信号无法有效抑制，故控制器鲁棒性和实时性较差。后续对于存在干扰力矩、非零惯量积等情况，需要进一步设计鲁棒控制器。反步法设计过程中中间控制律的具体形式对控制效果影响较大，后续可以对不同形式的中间控制律进行研究。文中只研究了SGCMGs平行安装时的姿态控制，对于如何提高SGCMGs的角动量利用率，以及非平行构型SGCMGs情况下的操纵律设计，也可以进行深入研究。

[1] 胡兵, 戈新生. 欠驱动卫星姿态稳定的非线性控制[J]. 北京机械工业学院学报, 2009, 24(1): 12-16.

[2] 庄宇飞. 带有非完整约束的欠驱动卫星控制方法研究[D]. 哈尔滨： 哈尔滨工业大学, 2012: 2-14

[3] 金磊, 徐世杰. 带有两个飞轮的欠驱动卫星姿态稳定控制研究[J]. 中国空间科学技术, 2009, 29(2): 8-16.

[4] POPESCU M, DUMITRACHE A. Stabilization of feedback control and stabilizability optimal solution for nonlinear quadratic problems[J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16: 2319-2327.

[5] 牛瑞艳, 许午啸, 刘金琨. 欠驱动机械臂滑模控制与实验研究[J]. 仪器仪表学报, 2016, 37(2): 348-355.

[6] 刘海颖, 王惠南, 陈志明, 等. 基于(w,z)参数化的欠驱动微小卫星姿态再定位控制[J]. 动力学与控制学报, 2008, 6(1): 14-18.

[7] 刘杨, 郭晨, 沈智鹏, 等. 欠驱动船舶路径跟踪的神经网络稳定自适应控制[J]. 控制理论与应用, 2010, 27(2): 169-174.

[8] BROCKETT R W. Asymptotic stability and feedback stabilization[M]. Boston: Differential Geometric Control Theory, 1983: 181-191.

[9] XU R, Özgüner Ü. Sliding mode control of a class of underactuated systems[J]. Automatica, 2008, 44(1): 233-241.

[10] 张志方, 董文强, 张锦江, 等. 控制力矩陀螺在天宫一号目标飞行器姿态控制上的应用[J]. 空间控制技术与应用, 2011, 37(6): 52-59.

[11] 贾飞蕾, 徐伟, 李恒年. 采用变速控制力矩陀螺的航天器姿态跟踪研究[J]. 空间科学学报, 2012, 32(1): 106-112.

[12] KWON S, OKUBO H, SHIMOMURA T. Pointing control of spacecraft using two single-gimbal control moment gyros[R]. Proceedings of the 27th International Symposium on Space Technology and Science, 2009: 47-51.

[13] 何昱. 基于单框控制力矩陀螺的敏捷小卫星姿态机动控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2011: 1-11.

[14] CROUEH P E. Satellite attitude control and stabilization: Application of geometric control theory to rigid body models[J]. IEEE Transactions on Automatic Control, 1984, 29(4): 87-95.

[15] TSIOTEAS P, LUO J. Control of underactuated spacecraft with bounded inputs[J]. Automatica, 2000, 36(8): 1153-1169.

[16] 戈新生. 欠驱动刚体卫星姿态运动规划遗传算法[J]. 动力学与控制学报, 2004, 2(2): 53-57.