倾斜轨道卫星极端外热流分析

张 好,曹建光,王 江,曾凡健

(上海卫星工程研究所，上海 201109)

0 引言

航天器在地球轨道上所受到的空间热流主要为太阳的直接辐射、太阳自地球的反照和地球的红外辐射。到达航天器的空间外热流与航天器在轨道上的位置及相对于太阳、地球的方位有关，同时也与航天器的轨道参数，如轨道高度、轨道倾角等因素密切相关[1]。卫星的极端外热流对确定卫星的极端工况以及热控系统设计有着重要影响，而对卫星极端外热流的准确分析目前还缺乏高效的方法。国内常以工况遍历的方式确定卫星极端外热流，工作量大，且不易准确找到卫星的极端外热流工况。

文献[2]中针对大椭圆轨道的太阳照射问题，结合光照角、椭圆轨道会日点位置、轨道阴影时间等诸多因素，理论分析了对地定向模式卫星在大椭圆轨道上的太阳投射状况，为大椭圆轨道太阳照射和在轨外热流分析提供思路和依据。文献[3]中根据角系数的假设条件和兰贝特定律推导出计算外热流的能束均匀分布法，该方法比常规的蒙特卡罗算法更高效、更准确。文献[4]中利用航天器设备在轨遥测温度值反演出航天器在轨瞬态外热流的导热反问题，建立反演航天器在轨瞬态外热流的数学模型，采用共轭梯度法求解导热反问题并从物理概念角度改进了共轭梯度法的迭代过程以增加其抗不适定性，并通过实际卫星在轨外热流数据验证该方法是可行的。文献[5]中采用反向蒙特卡罗法计算卫星在轨的外热流，研究了卫星在轨的瞬时地球反照率和反射率，通过与专业热分析软件I-deas作对比，证明该算法能有效计算外热流以及变化轨道外热流。文献[6]中针对天文探测卫星定点观测模式下的特定姿态，结合相关科学观测约束、整星能源和热控设计约束及轨道特点，分析多约束条件下的外热流变化规律，对比了有、无遮阳挡板时卫星外热流的差异，并通过虚拟热沉温度，分析了卫星各个舱板的散热能力。这些理论计算方法有些还处于研究阶段，不具备计算整星外热流的能力；有些模型较为复杂，计算难度较大，且对复杂卫星表面外热流的计算还需进一步深入。

研究表明:对于低轨卫星空间外热流来说，太阳辐射占据主导地位，地球反照和地球红外尽管相对比较小，但不容忽视。倾斜轨道卫星光照角的变化规律较为复杂[7-8]，而外热流受光照角的影响很大，倾斜轨道六面体卫星最小投射热流常发生在光照角(β角)为0°时，整星的最大投射太阳热流常发生在临界光照角处[9]。文献[10]中以散热面吸收外热流最小为目标函数，建立了基于六面体卫星的散热面最优化设计模型，并以某倾斜轨道六面体小微卫星为例，针对不同卫星热损耗分别得出了最优化的散热面布局。但是目前针对不同轨道参数对倾斜轨道外热流变化规律的影响研究甚少。

本文根据倾斜圆轨道六面体卫星极端外热流随光照角和太阳辐射强度变化的解析模型，通过与Sinda/Fluint仿真结果作对比，分析了不同计算时间单位对解析模型准确性的影响。同时研究了在不同轨道高度和轨道倾角的条件下，极端最大外热流和极端最小外热流的变化规律，为确定不同轨道卫星极端工况提供了帮助。

1 基本假设及初始边界条件

基本假设：

1) 对象为倾斜圆轨道六面体卫星(常见的六面体卫星结构[11]如图1所示)，三轴稳定对地定向(+X为卫星前进方向，+Z面对地，坐标系符合右手螺旋法则)，且不考虑轨道基本参数(轨道高度、轨道倾角)的漂移；

2) 不考虑除散热面之外的其他表面吸收外热流，且散热面的吸收率在一年内为定值；

3) 不考虑卫星外部设备对散热面的遮挡。

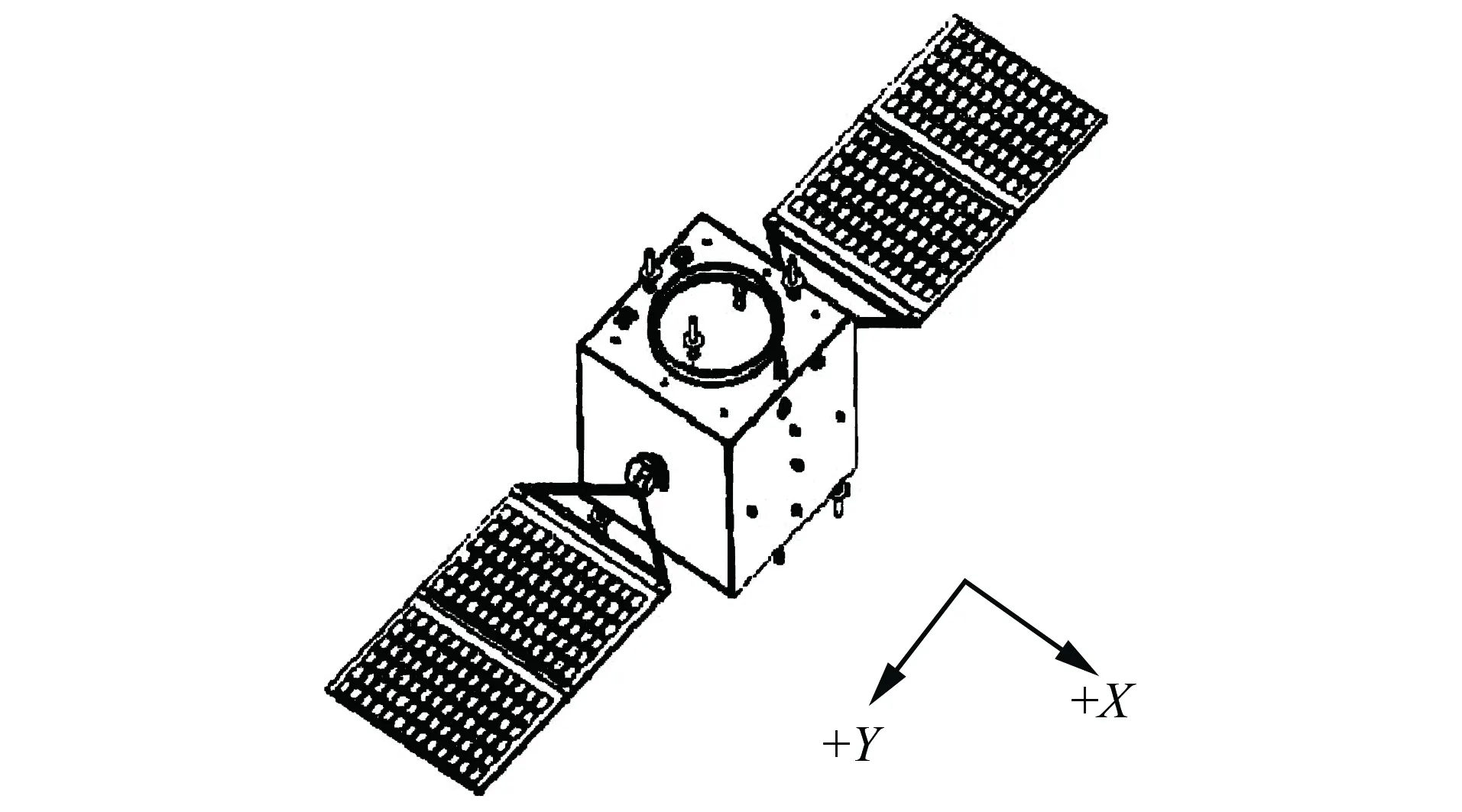
图1 常见六面体卫星结构图Fig.1 Regular structure chart of hexahedral satellite

卫星于2017年10月1日发射，计算时间从2017年10月1日到2018年9月30日。初始升交点赤经为0°，在临界倾角、某一特定轨道高度的条件下，光照角定义为[11]

式中：i为轨道倾角；δθ为太阳赤纬；αΩ为升交点赤经；αθ为太阳赤经。可以通过软件STK(Satellite Tool Kit)计算得到卫星1 a之内的光照角变化情况，如图2所示。

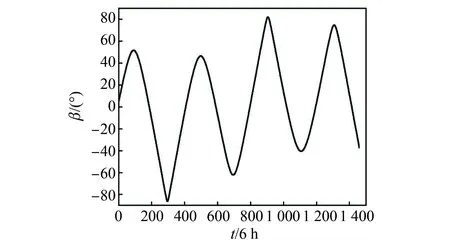
图2 1 a时间内β角随时间的变化规律Fig.2 Changing rule of beta angle in a year

2 解析模型

由于光照角的变化速率较快，假设以6 h为计算单位，光照角的变化矩阵表示为

(2)

式中：βi-j代表第i天内24 h的j等分时刻的光照角。

在一天的时间内，太阳辐射强度变化量基本可以忽略，因此一天内的太阳辐射常数取定值。为方便计算，太阳常数矩阵与光照角矩阵的形式一致，即

(3)

式中：Si-j代表第i天内24 h的j等分时刻的太阳辐射强度。

利用软件数据得到的从发射日起始的每天的太阳辐射强度，可以得到Si-j的拟合公式为

式中：t为距离发射日的时间，单位为d；S的单位为W/m2，拟合度R2=1。

根据文献[5]，取周期平均外热流，则太阳辐照外热流计算公式为

式中：α为各表面的吸收率；A为各表面散热面的面积；λ为会日点到卫星进入阴影区的夹角，卫星无阴影时λ取π；δ为逻辑判断函数，当光照角大于0时，δ-y=1，δ+y=0，当光照角小于0时，δ-y=0，δ+y=1。

卫星吸收地球反照辐射的模型比较复杂，针对不同的表面，计算公式具体如下所示。

X型表面(+X面和-X面)

(6)

式中：ρ为地球反照率；θ0为卫星所见地球视野半角(θ0=arcsinke，ke=Re/r，r为轨道半径)；b=min(π/2-θ0,π/2-|β|)。

Y型表面(+Y面和-Y面)分为阴影面和光照面。光照面和阴影面的计算公式分别为

(7)

sin|βi-j|]

(8)

Z型表面(+Z面和-Z面)

(9)

式中：Ex-ij、Ey-ij和Ez-ij分别为X型、Y型、Z型表面沿卫星视野的积分值(单位为W/m2)。

那么地球反照辐射吸收量为

(E+y-ijα+yA+y+E-y-ijα-yA-y)]×

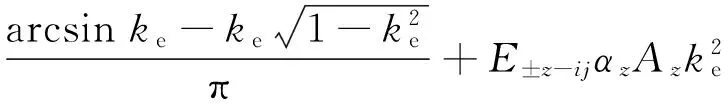
(10)

对于对地定向、三轴稳定卫星，各表面对地球红外的角系数基本不变，卫星各表面吸收的地球红外辐射密度为

q=EioΦ

(11)

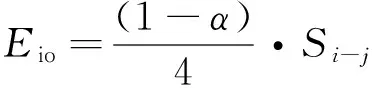
(12)

式中：Eio为地球表面红外辐射密度(单位为W/m2)；Ф为卫星各表面吸收地球红外辐射角系数。

3 模拟结果与分析

文献[9]中已经验证了模型的正确性。图3为以6 h为计算单位，临界倾角，某一特定轨道高度条件时，卫星各面吸收的外热流密度随时间变化曲线。

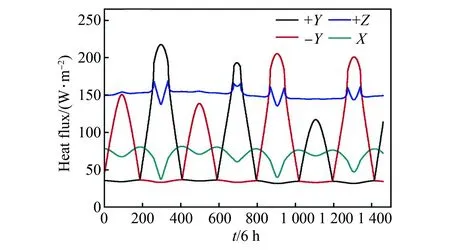
图3 各面吸收的外热流密度随时间的变化曲线Fig.3 Absorbed heat flux of each surface versus time

由图3可以看出，X型面的热流密度的均值小且较为稳定，相对应的X型面的温度低且稳定，适合作为主散热面；Y型面的热流变化较大，±Y表面轮流被照射，当+Y面达到最大外热流时，-Y面处于低外热流状态，当-Y面达到最大外热流时，+Y面外热流最小，因±Y表面可间歇性地处于极低外热流状态且有适中的均值，可考虑将其作为辅助散热面；+Z面热流稳定但因正对地球，受地球红外和地球发照辐射的影响较大，表面热流密度较大，而朝天面常为星箭连接面，故在散热面足够的情况，不考虑在Z型面设置散热面。

假定卫星各表面散热面面积如表1所示。

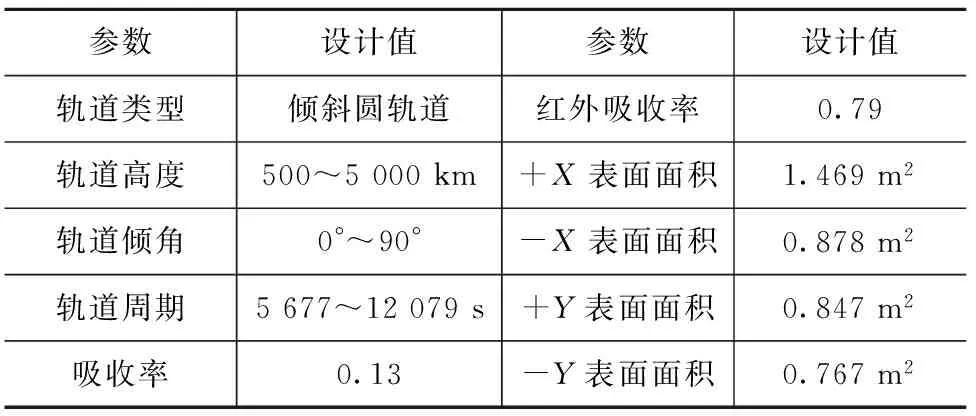
表1 轨道参数和各表面散热面面积

因倾斜轨道卫星受摄动力的影响，轨道光照角变化速率非常快，由图1可知，在某些特殊的情况下，一天内的光照角可变化2°以上，若采用较大的计算时间间隔，可能无法准确找到外热流的极端值，而采用较小的计算时间单位则有利于更准确地得到倾斜轨道卫星的极端外热流。但是计算时间间隔小会使计算量增大许多，为平衡计算量和结果的准确性，将对比计算时间单位为6 h和1 d时计算结果的差异，选择合理的计算时间间隔。

根据表1中的轨道参数和散热面面积，求得计算时间单位分别为6 h和1 d时，整星吸收外热流的变化情况，如图4和图5所示。

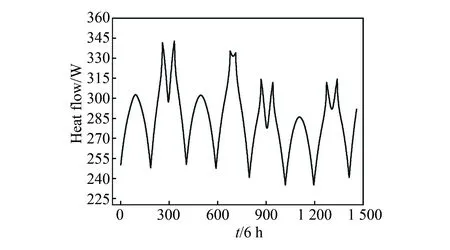
图4 计算时间单位为6 h整星外热流变化规律示意图Fig.4 Spacecraft heat flow changing rule at calculating time step of 6 hours

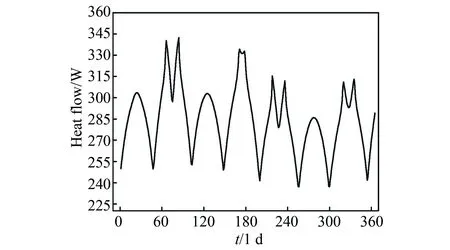
图5 计算时间单位为1 d整星外热流变化规律示意图Fig.5 Spacecraft heat flow changing rule at calculating time step of one day

由图5和图6可以看出，两者的变化规律(波峰波谷的数目以及相应时间)几乎一致，证明无论是以1 d还是6 h为时间单位，解析模型计算得到的结果都能完整显示整星外热流的变化情况。两种情况下外热流中的极端数值与软件模拟结果详见表2。

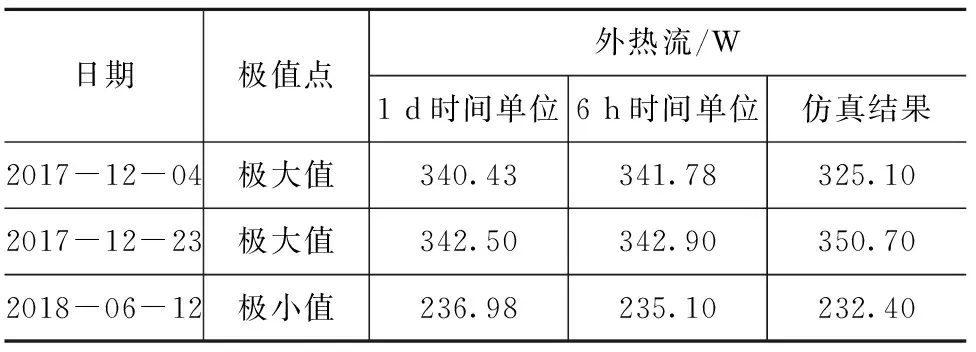
表2 在部分极值点处解析模型结果与软件仿真结果对比

从表2可以看出，在不同的极值点处，以6 h和1 d为计算时间单位所得到的结果相差不大，且并非以6 h为计算时间单位所得到的结果均比以1 d为计算时间单位时准确，两者与软件模拟结果的误差均在可接受范围之内。为节省计算所需时间，且便于后续研究,统一以1 d为计算时间单位。

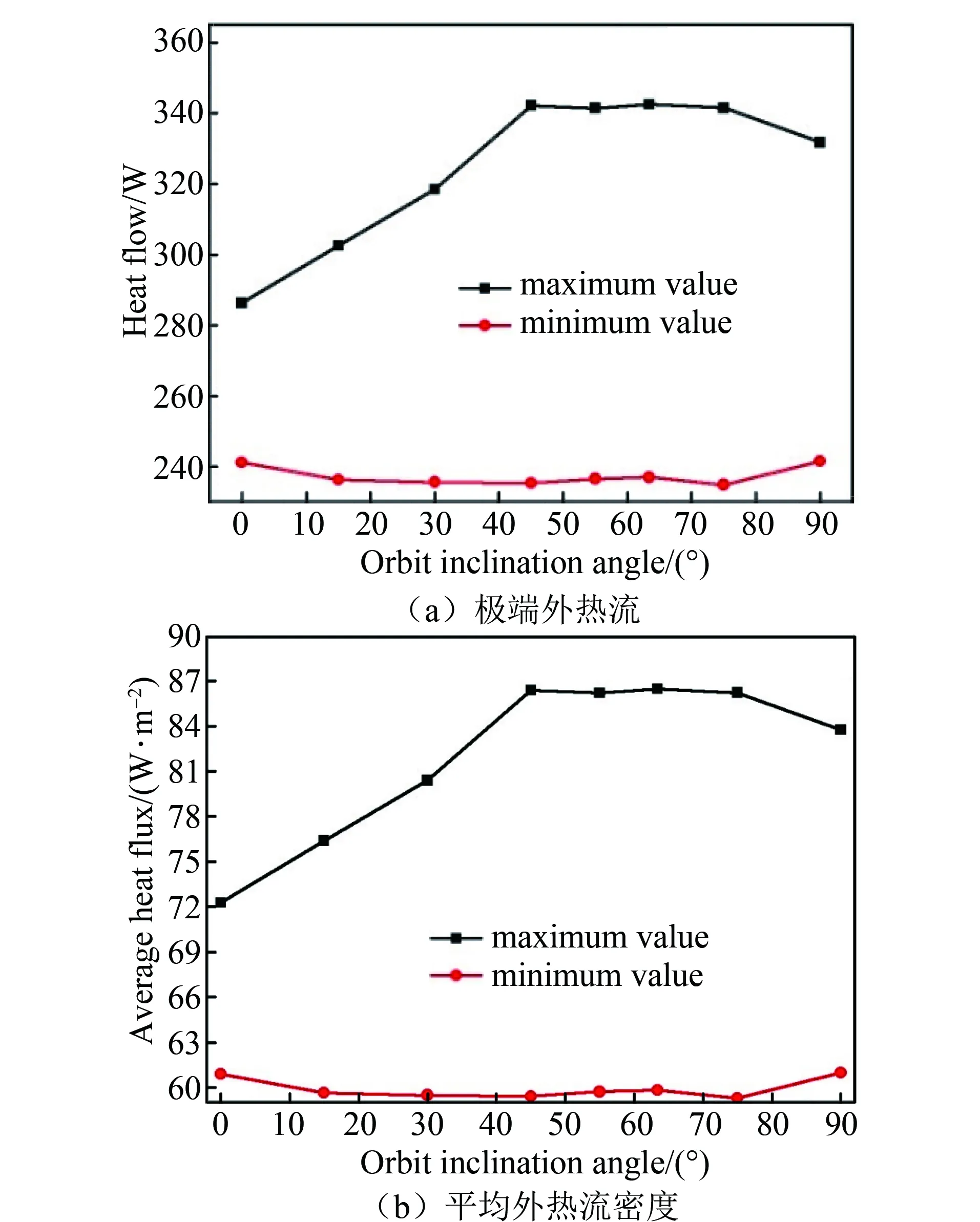
图6 特定轨道高度h=1 100 km、不同轨道倾角条件下的整星极端外热流和平均外热流密度变化曲线Fig.6 Spacecraft extreme heat flow and average heat flux versus orbit inclination angle at h=1 100 km

图6为当轨道高度不变时整星极端外热流和平均外热流密度随轨道倾角的变化规律曲线。可以看出，随着轨道倾角的增大，整星极端最大外热流逐渐增大，当轨道倾角大于45°以后，极端最大外热流趋于平稳,而整星最小外热流几乎不随轨道倾角变化。其原因是卫星达到极端最大外热流常在轨道临界光照角处，此时卫星运行一周时间内，随着轨道倾角的增大，进入阴影区的夹角λ逐渐增大，卫星在阴影区的时间逐渐减小，受到日照的时间增加，整星外热流增加。当轨道倾角大于临界光照角的余角(β*=58.53°，其余角为31.47°)时，卫星将不会进入地球阴影区，其周期平均外热流将不再随轨道倾角的变化而变化，而只受光照角和太阳辐射强度的影响。

为了验证该分析的正确性，对比40°光照角时仿真计算结果与图6中曲线的吻合程度，如图7所示。具体的最大平均外热流和最小平均外热流数值如表3所示。

图7 40°光照角的外热流仿真结果Fig.7 Simulation results of heat flow on the condition of 40° beta angle

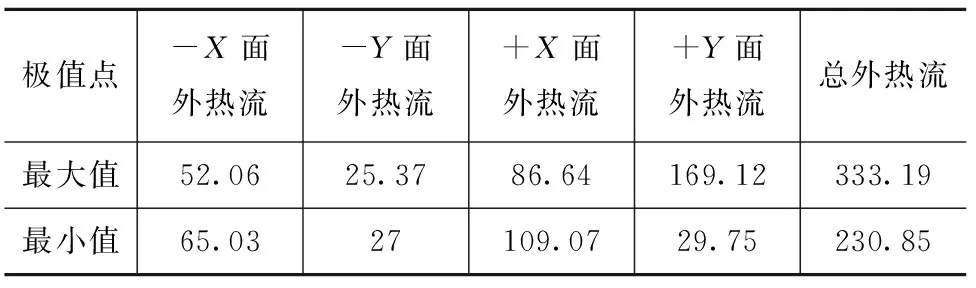
表3中最大外热流为333.19 W，与图6中最大外热流变化曲线相吻合；最小外热流为230.85 W，也与最小外热流变化曲线相吻合，证实了该分析结论的正确性。

而卫星达到极端最小外热流常在光照角为0°处，此时卫星在运行一周时间内，在阴影区的时间不会随着轨道倾角的变化而变化，故极端最小外热流几乎不受轨道倾角的影响。

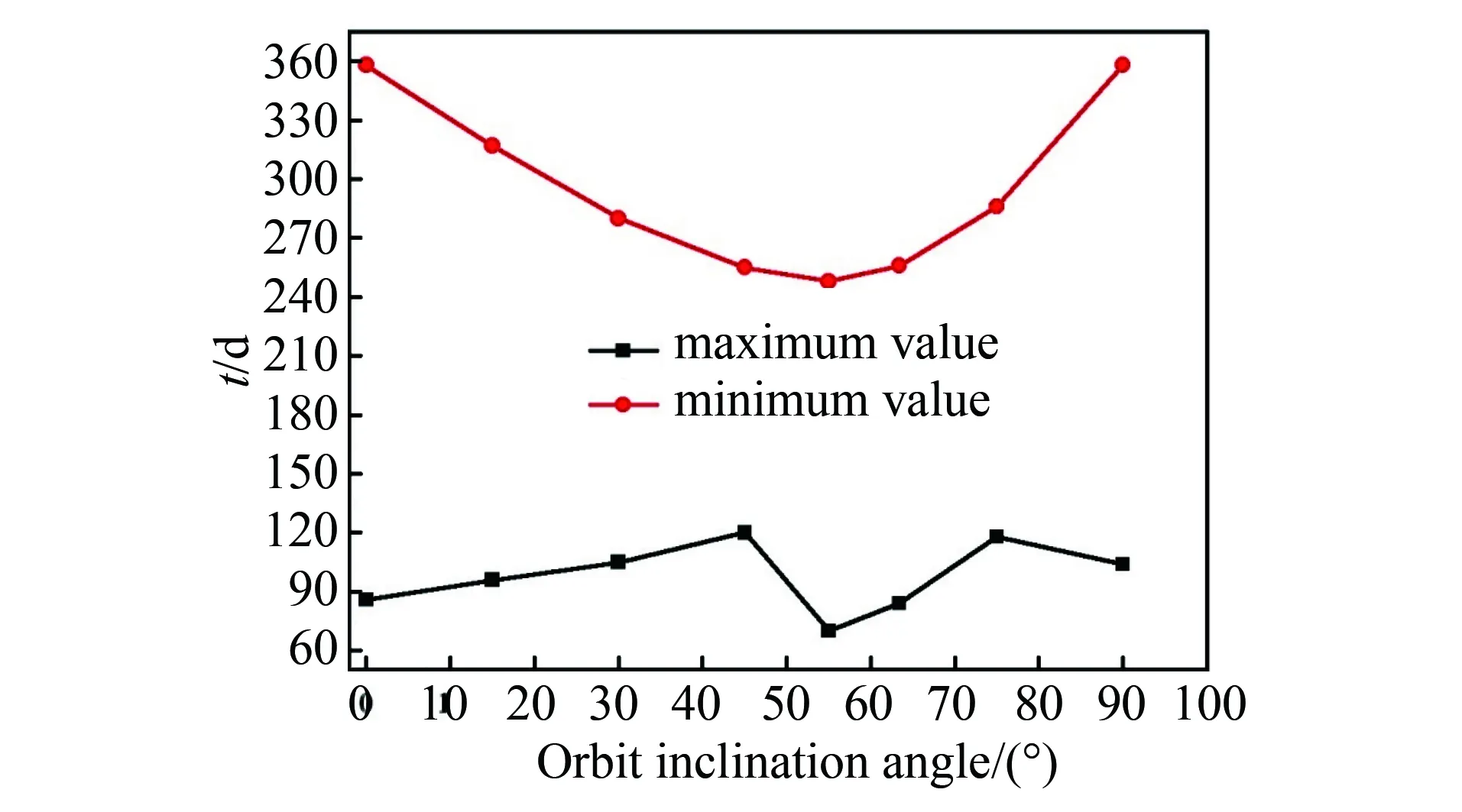
图8 特定轨道高度h=1 100 km、不同轨道倾角条件下 卫星到达极端外热流时间的变化曲线Fig.8 Time when spacecraft reaches extreme heat flow versus orbit inclination angle at h=1 100 km

图8为卫星到达极端外热流时距离发射日期的时间随轨道倾角的变化规律，可以看出整星在到达极端最小外热流的时间随着轨道倾角的变化而呈现U型变化，到达极端最大外热流的时间则无类似规律，较为随机。这是因为不同轨道倾角条件下，根据式(1)可知卫星达到临界光照角的时间与太阳赤纬的变化相对应，但公式中要得到太阳赤纬的值需要确定升交点赤经与太阳赤经之差的正弦值，故卫星到达临界光照角的时间与轨道倾角的关系不能用简单函数表示。

如图9所示，在轨道倾角为临界倾角63.4°的条件下，整星极端最大外热流和最小外热流均随着轨道高度的增加逐渐减小。因为随着轨道高度的增加，卫星的受晒因子逐渐增大，受到的太阳辐照量增加，而地球红外和地球反照量随着轨道高度增加而减小。因OSR的太阳吸收率小而红外吸收率高，地球红外辐射量占总外热流的比例较高，对总外热流的影响较大，因此总外热流逐渐减小。这一趋势在近地轨道中表现得更加明显，从图中可以看出，低轨时的总外热流减少速率要大于高轨。

图9 轨道倾角为63.4°，不同轨道高度条件下的整星极端 外热流和平均热流密度变化曲线Fig.9 Spacecraft extreme heat flow and average heat flux vary with orbit altitude at orbit inclination angle of 63.4°

如图10所示，在轨道倾角63.4°，不同轨道高度的条件下，卫星达到极端外热流的时间变化规律并不明显，处于波动状态，由式(1)可知，在轨道倾角确定的条件下，卫星到达临界光照角时，太阳赤纬与升交点赤经、太阳赤经的变化量有关，而升交点赤经的日变化量是轨道高度的复杂函数，故卫星达到临界光照角的时间与轨道高度关系不能用简单函数表示。

图10 轨道倾角为63.4°，不同轨道高度条件下 卫星到达极端外热流时间的变化曲线Fig.10 Time when spacecraft reaches extreme heat flux versus orbit altitude at orbit inclination angle of 63.4°

4 结束语

针对倾斜轨道卫星热控系统设计中极端外热流分析的实际需要，建立了圆轨道六面体卫星极端外热流随光照角和太阳辐射强度耦合作用的解析模型。与专业热分析软件Sinda的仿真结果作对比分析，验证了计算时间单位对模型准确性的影响。当计算时间单位为1 d时，从极端外热流的数值和卫星达到极端外热流所需时间的角度出发，研究了不同轨道高度和轨道倾角条件下的卫星极端外热流的变化规律。结果发现，在相同轨道倾角条件下，卫星极端最大外热流和最小外热流均随着轨道高度增加逐渐减少；在相同轨道高度的条件下，卫星最大外热流随着轨道倾角的增加逐渐增大然后平稳波动，而最小外热流随着轨道倾角的增加几乎不变；到达极端外热流的时间是轨道倾角和高度的复杂函数，处于波动状态。这为分析其他特殊而常用的卫星轨道的外热流变化规律提供了思路。

[1] 侯增祺, 胡金刚. 航天器热控制技术[M]. 北京: 中国科学出版社, 2007: 113-116.

[2] 江海, 钟奇, 刘伟. 大椭圆轨道太阳照射问题研究[C]∥第八届航天热物理会议论文集. 南昌:[s.n.], 2008.

[3] 张涛, 孙冰. 计算近地轨道航天器空间外热流的RUD方法[J]. 宇航学报, 2009, 30(1): 338-343.

[4] 宋馨, 张有为, 刘自军. 反演航天器在轨瞬态外热流的导热反问题[J]. 北京航空航天大学学报, 2015, 41(11): 2061-2066.

[5] 潘晴. 基于反向蒙特卡罗法的飞行器空间外热流计算[D]. 上海: 上海交通大学, 2012.

[6] 周宇鹏, 赵欣, 孙腾飞. 天文探测卫星定点观测模式外热流变化规律分析[J]. 航天器工程, 2013, 22(4): 49-55.

[7] Fortescue P, Swinerd G, Stark J. Spacecraft systems engineering[M]. 李靖, 熊蔚明, 赵小翔, 等, 译. 北京: 科学出版社, 2015.

[8] 章仁为. 卫星轨道姿态动力学与控制[M]. 北京: 北航出版社, 1998: 210-213.

[9] 赵欣. 卫星热设计中β角在不同轨道下的变化规律分析[J]. 航天器工程, 2008, 17(3): 57-61.

[10] 黄金印, 赵欣, 麻慧涛. 六面体小微卫星散热面最优化设计[J]. 航天器工程, 2013, 22(6): 48-52.

[11] Gilmore D G. Spacecraft thermal control handbook[M]. 2thed. EI Sefundo: The Aerospace Press, 2002.