空间机械臂动力学特性的仿真分析研究

韩东宇，陈欢龙，余春华

(1. 南京理工大学 理学院，江苏 南京 210094；2. 上海宇航系统工程研究所，上海 201109)

0 引言

航天飞行器的研发设计中，往往无法全面考虑外太空恶劣工况下所出现的突发状况，在航天器在轨运行中，也容易发生表面结构脱离，燃料不足，模块单元分离或预设性动作失谐等情况，这些通常需要空间机器人的协助操作。特别是遇到大型空间组装及搬运任务时，这些在失重环境下的程序性动作显得复杂而难以满足功能性需求。因此空间机器人的研制对于在轨操作有重要的意义。

为实现航天器研发及运行过程中所需的维修、加注、回收等有效利用，同时为减少突发劳损等航天器非自然破坏而引发的高昂成本，以及减小未来宇航员可能发生的舱外作业的危险性，空间机械臂的研究逐渐进入各个国家航天领域的视野[1-2]。

图2 平移关节锁定时的机械臂D-H坐标系Fig.2 D-H coordinate system of manipulator with translational joint locking

空间多自由度机械臂的研究除了需要克服失重条件，另一个难点在于漂浮基座空间位置的不确定性，即基座的可移动性，使机械臂的运动多了移动导轨或者气浮平台这个冗余自由度，在完成规定动作的目标任务时，如何分配运动指令到各个关节和移动基座，成为核心的技术指标[3]。另外，卫星基座的运动还要考虑到多种非确定性扰动因子。这就使通常的数学解析或全物理实验都受到限制[4]。数学解析或纯数字仿真无法真实还原太空环境，尤其是瞬间碰撞的数据无法通过建模准确测出；而全物理实验中的重力补偿与完全失重区别较大不能准确模拟，所以国际上目前最新的方法多是采用数学仿真加实验平台的半物理方法[5]。

用数学仿真完成动力学过程，将运动指令直接赋给实验平台的电机驱动，将接触碰撞的力学数据反馈给仿真控制平台，进行运动补偿，从而实现空间机械臂移动路径的跟踪规划。而数学仿真的主要困难在于多刚体系统的动力学特性分析。目前机械臂的研究分析一般从结构学、运动学及动力学三方面展开[6]，运动学方程和动力学方程是机械臂运动规划的基础。

对多关节运动机构的研究，通常方法是分别在每个坐标系上建立空间坐标系，利用齐次坐标转换的方法，求解出每个关节的位置和姿态，直到末端执行机构的位姿[7]，即Denavit-Hartenberg方法，但是建立坐标系方案的细节也有很多种[8-9]。

本实验研究的对象为星体基座带三臂的空间机械臂系统，即给定各个关节值求末端操作器的物理量。主要困难仍然是由于自由飘浮基座的位置在关节角变化过程中同时变化，不能简单用地面固定基座的方法求解，需要综合考虑基座位姿变化带来的影响[10]。在研究空间或移动基座机械臂问题上，较为通行的方案是在固定基座机械臂的运动学方程基础上，乘以一个基座随移动导轨运动的参数矩阵，从而全面反映整体自由度坐标系的运动特性[11-12]。但此方法易出现冗余自由度，难以实现运动指令分配的自动化[13]。而这一问题的解决主要依靠闭环控制系统完成，通过机械臂的动力学仿真反馈运动数据，进行运动补偿，以实现运动分配自动化。

本文将探讨运用SimMechanics工具搭建动力学系统平台，进而封装成子模块，嵌入到控制系统中调试，进行路径规划，并加载到仿真机中运行。并应用Matlab和ADAMS作联合仿真[14]，进行动力学特性的对比分析。

1 机械臂移动路径系统的原理模型

1.1 参数化多臂系统建模

机械臂抓捕系统动力学建模主要包括三个部分：多机械臂系统的建模、操控飞行器平台的建模以及操作目标飞行器的建模。机械臂抓捕系统的动力学模型示意图如图1所示。

图1 机械臂抓捕系统动力学模型示意图Fig.1 Schematic diagram of the dynamic model of robotic arm arresting system

空间操控机械臂共有9个关节，采用3-1-1-1-3的偏置式布局方式，9个关节中包含7个转动关节和2个移动关节，其中各转动关节的关节变量分别为θ1，θ2，θ3，θ4，θ5，θ6，θ7。当机械臂执行抓捕任务时，需将两个平移关节锁定，此时坐标系定义如图2所示。将机械臂的展开状态定义为初始参考构型。

利用机构动力学仿真分析商业软件ADAMS，建立全参数化的多机械臂系统动力学模型。利用Matlab/Simulink与ADAMS联合仿真，进行运动学、动力学以及平台和多臂系统的协调控制分析。其核心问题在于核验仿真结果的正确性，所以要基于数学动力学方程的推算与对比。参数化机械臂动力学模型的展开和收拢效果示意如图3所示。

图3 机械展开和收拢效果示意图Fig.3 Schematic diagram of mechanical unfolding and folding

1.2 机械臂抓捕动力学仿真分析

机械臂动力学仿真分析主要包括以下几个部分：机械臂位姿反解、关节空间的路径规划、笛卡儿空间的路径规划、飞行器的平台控制、机械臂与平台的协同控制、末端工具位姿调整等。

机械臂路径规划、位姿反解程序、平台姿态控制在Matlab/Simulink中编写程序实现，机械臂动力学模型在ADAMS中实现，通过ADAMS/Control模块与Simulink控制程序进行信息交互，Simulink向ADAMS输入机械臂每个关节的运动指令和操控飞行器平台的控制力矩，ADAMS向Simulink反馈状态量，完成联合仿真。

1.3 机械臂的路径规划与抓捕及其主要问题

对机械臂进行路径规划时，机械臂的基座坐标系与抓捕目标坐标系是相对固定的，因此需要将操控飞行器平台与大地固定连接，而且需要锁定机械臂的两个平移关节，并锁定第二个转动关节。

考虑单臂的路径规划。机械臂处于初始构型时，7个转动关节相对于D-H坐标系下的关节角为[180° 0° 70° 90° -70° 0° 45°]。

由此可实现以下全过程的仿真分析：机械臂末端工具由起始位置到目标特定点的各个关节的空间路径规划；机械臂末端到达预期位置和姿态时，末端执行机构接收指令开始工作，实施抓捕动作。

其中主要问题在于核验仿真分析的正确性，首先对仿真所基于的数学原理进行分析，之后再运用两套仿真系统的结果数据作对比。

2 机械臂系统动力学建模

2.1 算法原理模型

通过对比国内外常用机械臂建模方法的优劣，结合研究方向，采用基于Lagrange的建模方法。

基本假设：本实验研究的机械臂系统为刚体系统，且各零件之间彼此刚性连接；机械臂与载体及每条机械臂的臂与臂之间只有一个转动关节；忽略重力梯度影响。

2.2 运动学方程

采用基于D-H参数法的正运动学建模，正运动学方程可以描述相邻连杆坐标系之间的相对空间关系，从而可以根据每个连杆之间的相互关系，由基坐标系递推到末端坐标系的表达式，即可推导出正运动学方程。

考虑基座惯性姿态由俯仰角θb、滚动角φb和偏航角ψb给出，则从惯性坐标系到基座坐标系的坐标转换矩阵为

(1)

三条刚性臂的D-H参数一致，其中O0-x0y0z0坐标原点与安装坐标系原点转换矩阵为固定值。

对于任意一个满足前述假设的多自由度运动体系，定义各种运动学参数如下。

R安装坐标系原点Oc关于大地坐标系O0x0y0z0的位置矢径。

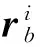
v0安装坐标系原点Oc关于大地坐标系O0x0y0z0的瞬时速度。

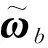
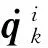
基于上述定义，可以给出多自由度上任一关节点的角速度和角加速度，以及任一点的位置，进一步可以求出其速度和加速度。

第i组机械臂中第j节臂的质心位置为

(2)

第i组机械臂中第j节臂的质心线速度为

(3)

第i组机械臂中第j节机械臂的质心角速度为

(4)

2.3 动力学方程

三臂多自由度机械臂系统的拉格朗日公式为

(5)

系统的动能为

(6)

为计算方便将T写成如下形式

T=T0+T1+T2

(8)

(9)

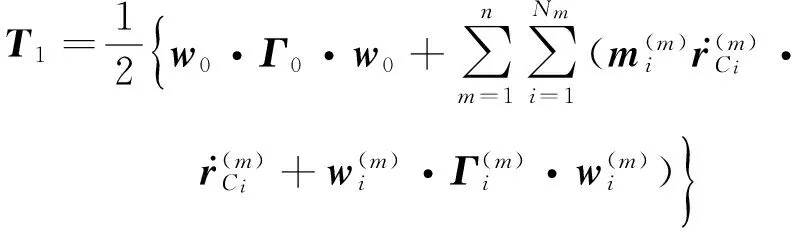
(10)

(11)

系统的广义坐标选为

(12)

式中：θT为角位移矩阵。

根据需要改写为

式中：δ0为本体的欧拉角，q(m)表示第m臂的关节角，系统动力学方程的形式为

(16)

式中：C为一个N×1维矢量，包含了微重力环境下所有的非线性速度项；Q为一个N×1维广义力矢量。H,C和Q为线位移σ0和角位移θ以及其一次求导的方程式。如除本体外，施加在系统其他部分的外力为零，则Q可以表示为

(17)

式中：0fs和0ns为施加在飞行器本体上的静力；JQ为一个N×N的雅克比矩阵；τK×1为施加在各个臂的每个关节的控制力矩。为了获得多臂多自由度空间机械臂的显式动力学表达形式，且减小计算的复杂度，在求解质量矩阵H、非线性速度项C和广义力Q之前，需要做一些预计算处理。

质量矩阵H是加速度项的系数，经过计算得到的Hij为

(18)

此处左上标代表的是进行微分的坐标系，如果缺省表示惯性坐标系。

式中的非线性速度项为

(19)

式中：C1为广义位移一次求导的系数矩阵；C2为广义位移的常量矩阵；而

(20)

(21)

如果除了本体，施加在系统其他部分的外力为零，雅克比矩阵JQ由下式决定，即

(22)

式中：T0为本体坐标系到惯性坐标系的转换矩阵，S0为欧拉角速率到角速度的转换矩阵；Ik×k为k阶单位阵。定义如下

(23)

0ω0为本体坐标系下的角速率矩阵。

至此，便完成了完整的动力学求解过程。

3 基于Matlab与SimMechanics模块的动力学算法验证

3.1 动力学模型的构建

这里利用Matlab中的Simulink和SimMechanics作机械系统的建模和仿真分析，并将其模型的实时处理结果加载到仿真机中做硬件在回路的仿真。

SimMechanics内嵌于Simscape中，并扩展了其三维机械系统建模的能力，并应用sensor和source模块将其拓扑模型的物理信息反馈于控制系统，实现对闭环控制算法的开发。

由于每一个支链的结构都是相同的，并且支链内部的各个参数涉及转动方向和移动方向的计算。坐标系以模型的初始状态为基础，根据D-H参数，为方便调试，每条支链在实体模块中建立一个过渡坐标系CS3,并用变量名表示。

Position标签下的CS1、CS2、CG、CS3根据初始状态计算，CG为每个实体初始重心，CS1为该杆与固定平台或上一实体连接的铰点坐标，CS3为初始状态下该杆的长度，CS2为理论上与移动副连接的点坐标，因此，把它和CS1的Show Port勾选。方括号中的实际坐标值根据参考的坐标系，结合D-H参数实际测量后填写。变量采用结构体(Struct)形式。Orientation下的CG、CS1、CS2和CS3，主要是运动副坐标系的旋转方式，具体参数值的设置主要根据D-H参数定义的旋转变换矩阵。同时将每个臂节的质量惯量参数设计成变量输入到对话窗的Mass和Inertia一栏中。

定义好一个臂节的参数后，就将其封装成一个子模块，嵌套进一个七自由度机械臂的模块，最后一个臂节的实体中CS2的参数涉及到末端位置姿态数据输出，要添加额外的关节传感器接口。

图4为单只机械臂一个臂节的内部模块选用及构架图，相应的英文名称为具体选取的模块类型，主要包括actuator(驱动模块)，用于传输外部驱动数据如速度、力、力矩等，通过图中的接口drivermo由外部控制系统输入；sensor(实体传感器模块)测出revolute(关节模块)的运动数据包括角度angle、角速度avelocity，并通过该名称的接口反馈给外部控制系统，eye为用户对相应实体的定义，因末端抓捕器含手眼视觉，所以定义为“eye_00”，实体内部参数的定义上面已经说明，当勾选“Show Port”时，将作为接口连接其他臂节，CS3未勾选，只作为过渡坐标系统，便于不同型号下D-H参数的输入。

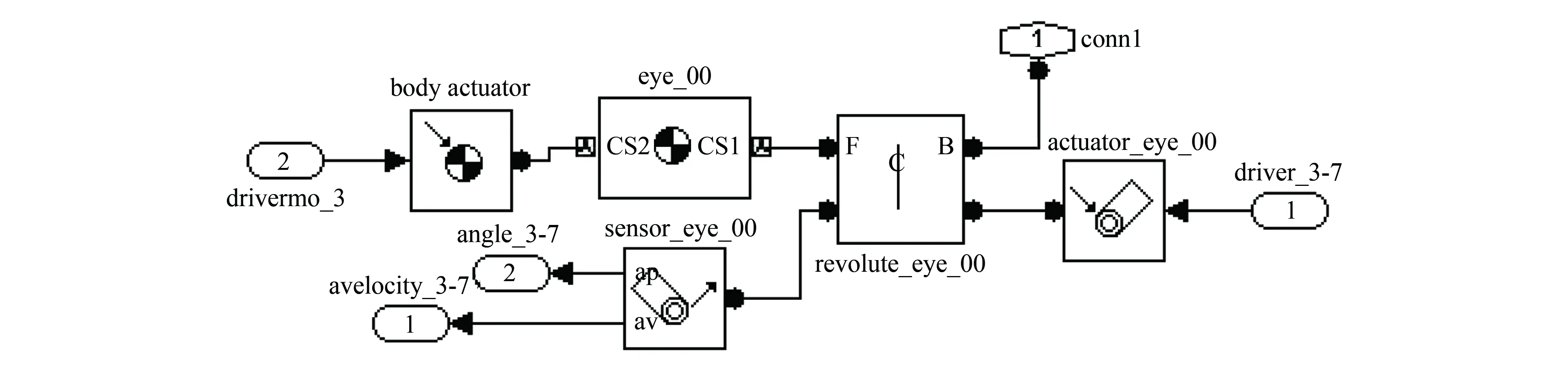
图4 单只臂节的内部架构Fig.4 Internal structure of single arm

图5 一条机械臂的内部架构Fig.5 Internal structure of a mechanical arm

图6 整个平台动力学的架构Fig.6 Architecture of the whole platform dynamics

图5为七个臂节通过名为“conn”的接口首尾相接构成一个完整的机械臂arm，并和其余三个机械臂共同接于ground坐标系下的星体安装接口。其中每一个模块为一个臂节，由图4的臂节详图缩合而成，其输入端口需从控制系统取得每个臂节的驱动参数，由driver接口输入，并通过键标指号“D_A～D_G”引导，其输出端口由“avelocity”“angle”端口向控制系统反馈每一个关节的角速度和角度运动参量，通过“A1～G1”“A_2～G_2”引导。

最后将完全相同的三条七自由度机械臂根据接口位置定义连接到操控飞行器平台上，如图6所示。将机械环境变量中的重力输入选项勾掉，设置固定基座的中心坐标默认为零，平台与其连接的关节选用Six-Dof 六自由度连接，表示飞行器完全不受约束，其中“Env”代表机械环境变量，ground为惯性坐标系，XY_MoForce为控制系统传入的飞行器平台的驱动数据，CS1接口为要向控制系统输出星体各项运动参量的接口，包括位置p，速度v，角速度ω，姿态矩阵R和加速度a；并可通过显示器将其数据显示为随时间变化的运动曲线。对于其他各条机械臂，除了关注各个关节运动数据外，还特别关注末端的运动数据,包括位置、姿态、移动速度、角速度。

SimMechanics模块最好由每个模块本身功能及原始英文加编号定义，便于Simulink中的控制系统以及和其他软件的联合调用，切不可译成中文，否则会出现调用失败。

将整个平台动力学SimMechanics模块搭建好后，就可以设置输入输出接口，然后串行到控制系统中，接收外部输入的驱动信号、输出位置、速度、姿态等反馈信号，进行控制调试。

3.2 正逆运动学以及正动力学的验算

将正逆运动学方程由3.2节推导的公式编入程序，写成m文件，或写入Embeded函数中，输入不同的关节角指令，查验每个关节的位置姿态矩阵，并将运行结果输出到workspace，和SimMechanics每个实体的传感器sensor检测到的运动参数作比对，监视其输出结果，核验动力学模型的正确性。

为核验动力学模型的正确性，将ADAMS和SimMechanics搭建的动力学模型的运算结果进行比对，在第一个关节角处输入一个正弦力矩驱动，查验各关节角度、角速度以及角加速度10 s内运行的变化曲线，仿真结果如图7～9所示。

图7 单只机械臂各个关节角10 s内的变化Fig.7 Variation of each joint angle of the single arm in 10 s

图8 单只机械臂各个关节角角速度10 s内的变化Fig.8 Variation of angular velocity of each joint angle of the single arm in 10 s

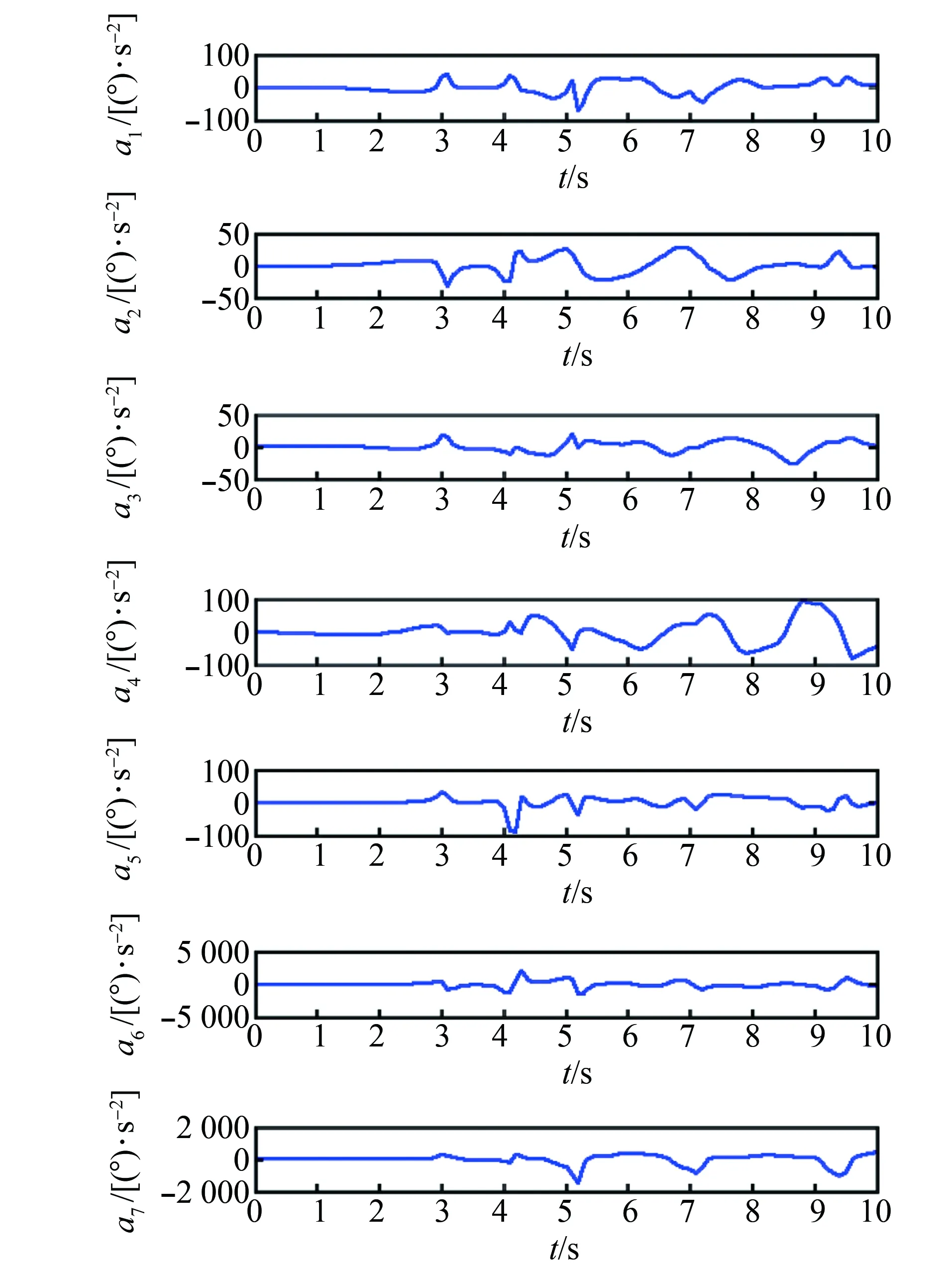
图9 单只机械臂各个关节角角加速度10 s内的变化Fig.9 Variation of acceleration of each joint angle of the single arm in 10 s

经过核验，发现在不同关节输入不同驱动下，其运算后的角度、角速度及角加速度曲线与ADAMS验算的仿真曲线基本一致。图10～11为在星体上的第一安装坐标系原点上输入一个正弦驱动后，其末端的工况曲线，包括机械臂末端相对于本体基座的姿态角(图10)，相对于平台的角速度(图11)。从而验证了两种动力学模型构建的正确性。

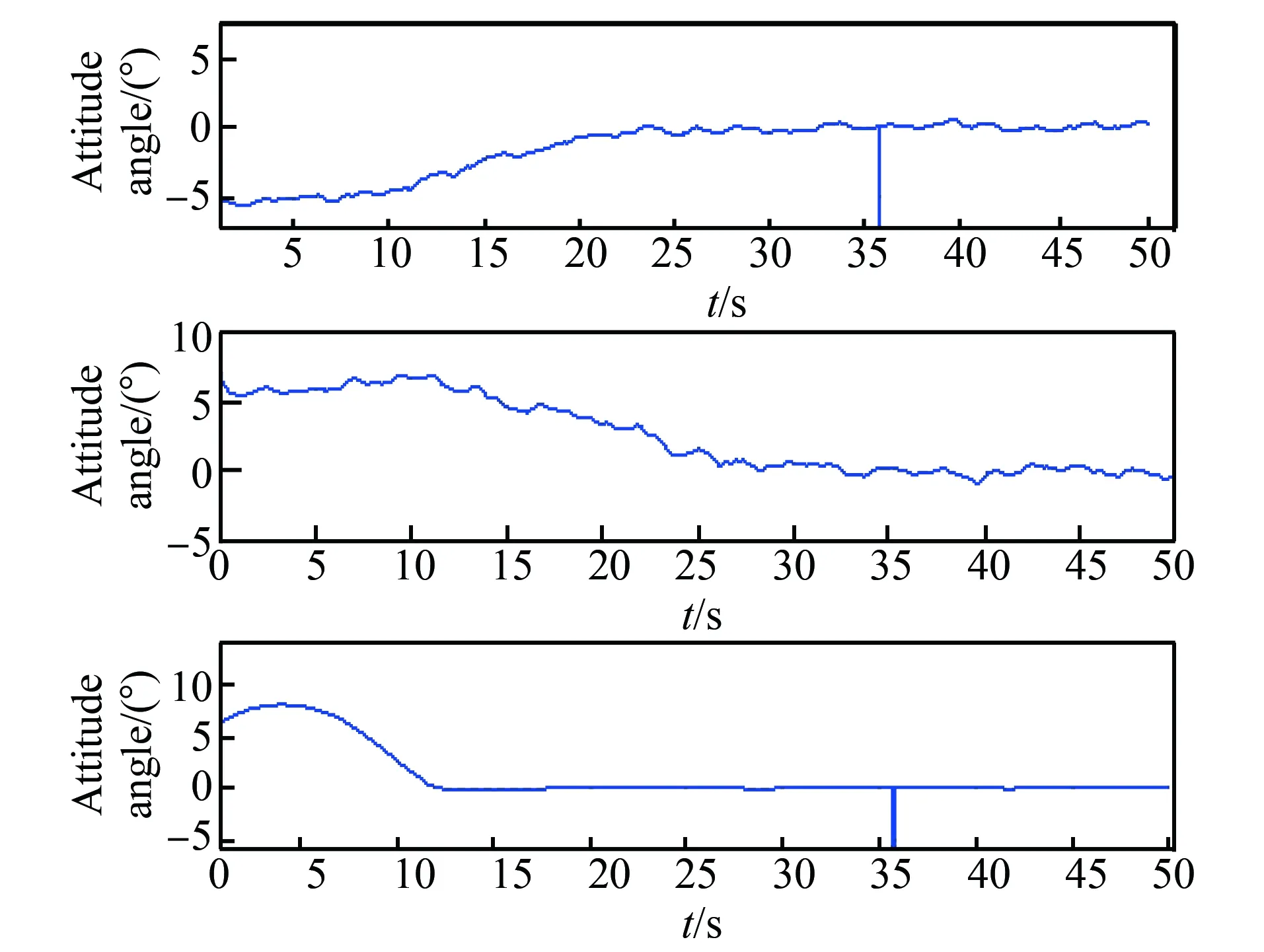
图10 机械臂末端相对于平台的姿态角Fig.10 Attitude angle of the manipulator relative to the platform

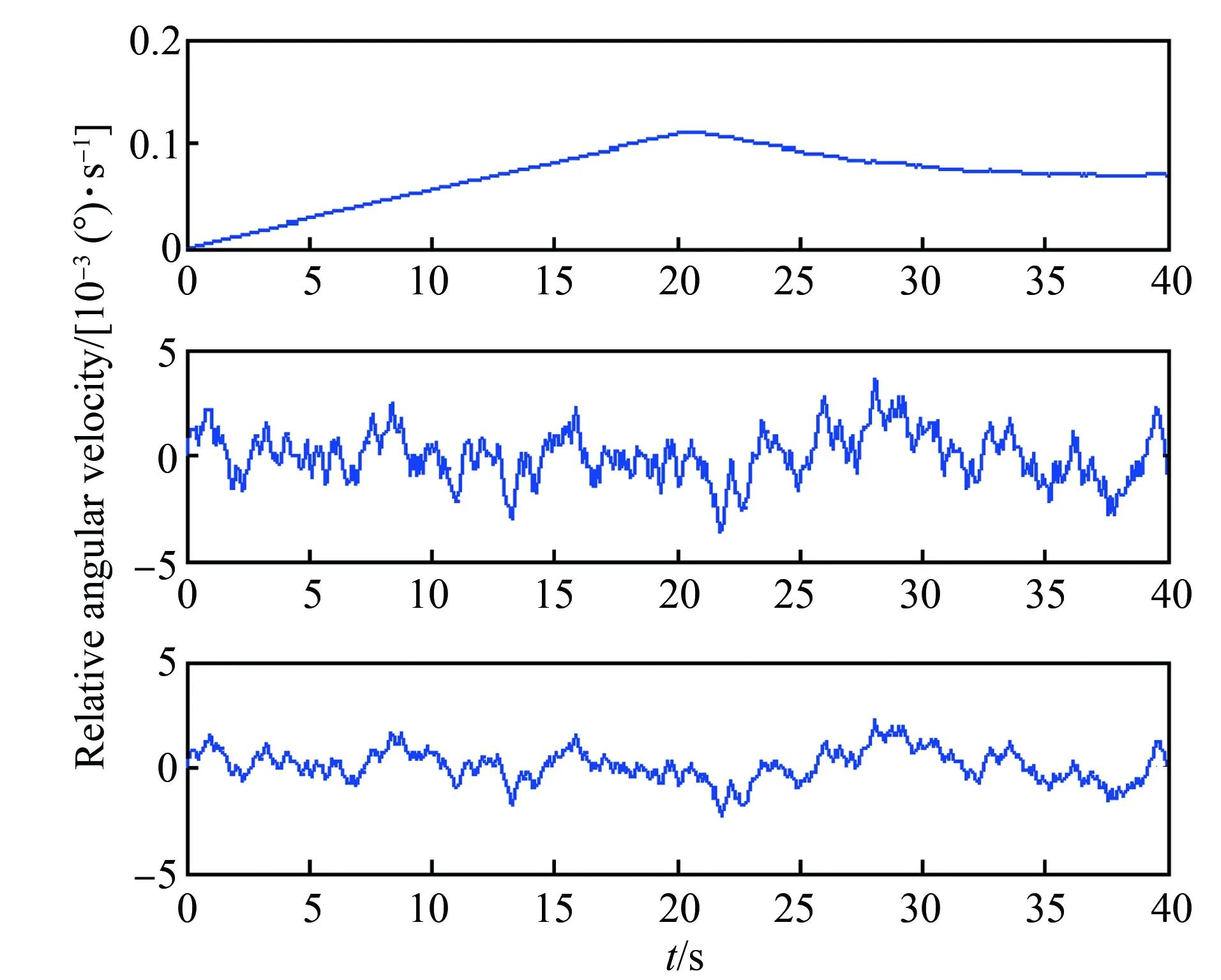
图11 机械臂对于平台的相对角速度Fig.11 Relative angular velocity of the manipulator to the platform

4 结束语

本文首先应用拉格朗日公式推导了空间平台带3个机械臂的运动学方程和动力学方程，并利用SimMechanics工具箱以及ADAMS软件分别实现了对空间操控飞行器带三个七自由度机械臂的动力学模型的搭建，然后通过算法程序计算了末端执行器的静位姿态，核验了运动学理论方程的正确性，再通过在不同的关节处输入不同的关节驱动，观察各个自由度的工况曲线，核查动力学模型的正确性。

动力学模型的搭建，实现了对空间机械臂在轨操作和抓捕等的仿真和运动模拟，为研究空间机器人问题奠定基础，并可嵌入到控制系统中，实现闭环联合仿真测试，也可以为进一步半物理实验做好基础准备工作。

该多自由度机械臂动力学特性的理论分析和数学仿真是机器人学应用的核心问题。在多体动力学的诸多领域，该多自由度机械臂有广泛的应用前景：航天领域如在轨操作、舱外维修等；医学、建设、机械、生活领域，如医用助力臂、车间冲压机械手、自动焊接设备、吊车抓捕、家用洗碗机等，建立模型时只需在机械环境变量中设置重力惯性环境。

[1] 翟光, 仇越, 梁斌, 等. 在轨捕获技术发展综述[J]. 机器人, 2008, 30(5): 467-477.

[2] 黄涣. 空间机器人功能行为建模与飞行任务仿真[D]. 长沙: 国防科技大学, 2009.

[3] 赵阳, 张大伟, 田浩, 等. 飞行器在轨任务[J]. 上海航天, 2009, 26(3): 38-41.

[4] SHAO Z F, TANG X Q, CHEN X, et al. Inertia match of a 3-RRR reconfigurable planar parallel manipulator [J]. Chinese Journal of Mechanical Engineering, 2009, 22(6): 791-799.

[5] 胡俊峰. 柔性机器人机构动力学分析及振动控制研究[D]. 广州: 华南理工大学, 2010.

[6] NIKU S B. Introduction to robotics analysis, control, applications[M]. 2th ed. Cincinnati: Prentice Hall, 2001.

[7] 黄献龙, 梁斌, 陈建新, 等. EMR系统机器人运动学分析和求解[J]. 宇航学报, 2001, 22(2): 18-25.

[8] 梁斌, 刘良栋, 李庚田, 等. 空间机器人的动力学等价机械臂[J]. 自动化学报, 1998, 24(6): 761-767.

[9] 王鸿鹏, 洪炳熔. 自由飞行空间机器人通用运动学模型及其仿真[J]. 宇航学报, 2000, 21(3): 45-51.

[10] 胡松华, 薛力军, 强文义, 等. 空间机器人系统动力学建模与控制仿真研究[C]∥中国控制与决策学术年会论文集.南京: [s.n.], 2005: 1978-1987.

[11] 于登云, 孙京, 马兴瑞. 空间机械臂技术与发展分析[J]. 航天器工程, 2007, 16(4): 1-8.

[12] 范成建, 熊光明, 周明飞. 虚拟样机软件 MSC. ADAMS应用与提高[M]. 北京: 机械工业出版社, 2006.

[13] 张国亮. 空间机器人遥操作中基于视觉的局部自主控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.

[14] ROVNER R. SimMechanics 3 getting started guide[M]. Massachusetts: Intel Robot System, 2009: 1-199.