模糊PID控制无人自转旋翼机飞行姿态仿真

苏中滨，章宗鑫，马晨茗，高 睿

（东北农业大学电气与信息学院，哈尔滨 150030）

自转旋翼机（简称旋翼机）以旋翼被动自转提供升力，纵向螺旋桨推/拉产生前进动力。旋翼机具有短距离滑跑起飞、低速着陆、操作灵活、结构简单和安全性能高等特点。无人旋翼机旋翼通过相对来流作用自转产生升力，载重量大、低空性强、故障率低，适应农业航空植保作业要求，在农药喷洒、低空农情监测作业中优势明显。

飞行控制系统中经典PID控制占重要部分，精度高，易实现，但经典PID控制在模型非线性和参数时变性情况下控制效果不佳。载荷变动量超过机体自身重量时，受外界干扰经典PID控制系统易产生振荡，飞行失稳。模糊PID控制是通过不断检测姿态角误差e和误差变化率ec，根据模糊控制规则在线实时对整定PID控制器3个参数，解决经典PID在参数变化时控制效果不佳问题[1]。因此，模糊PID控制同时具有经典PID高精度与模糊控制快速响应性和适应性。本文为旋翼机姿态控制采用模糊PID控制，针对该姿态控制器MATLAB数字仿真。结果表明，采用模糊控制姿态控制器能够对旋翼机姿态被控对象准确跟踪，鲁棒性和自适应性强。

1 旋翼机机体分析与姿态模型

1.1 旋翼机机体结构分析

旋翼机结构主要有：无动力旋翼、推力系统，全动垂尾，起落架和控制系统。

旋翼机在发动机牵引或推动下滑跑或飞行，获得迎面气流吹动旋翼旋转获得升力。旋翼机旋翼桨叶剖面为正迎角，飞行时桨盘平面后倾。旋翼机结构如图1所示。

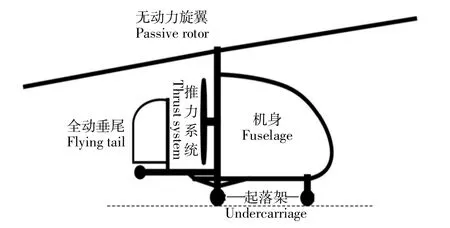
图1 旋翼机结构Fig.1 Frameof UAV

无动力旋翼是旋翼机主要升力装置，旋翼机飞行时旋翼被动旋转提供旋翼机全部升力。由于旋翼机桨距固定，旋翼机机身姿态俯仰与横滚需通过直接操纵桨盘相对姿态角实现。

全动垂尾是旋翼机方向舵，主要用于控制机身航向，提高机动性和操纵效率。

控制系统包括各类传感器，陀螺仪，微控制器等硬件设备，用于实现旋翼机无人飞行控制[2]。

自转旋翼机飞行操纵特性和固定翼与直升机类似，旋翼机通过发动机产生推力或者牵引力使机体向前运动获气动升力，依靠操纵方向舵控制机体飞行航向，该控制方式与固定翼飞行器相似；在横滚和俯仰姿态操控上，旋翼机根据旋翼桨盘倾斜实现机体姿态变化，该控制方式与直升机相似。旋翼机旋翼转速不固定，取决于滑跑或飞行时迎面气流速度和桨盘迎角倾角，与固定翼飞行器和直升机不同。

1.2 旋翼机姿态模型

飞行器在空间运动时视为六自由度刚体，飞行时姿态运动方程可分为运动学方程和动力学方程，方程组分别如下所示：

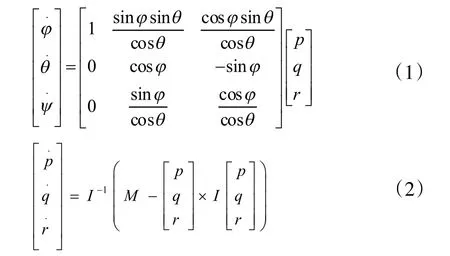
式中，p，q，r依次为滚转角速率、俯仰角速率及航向角速率，φ，θ，Ψ依次为滚转角、俯仰角和航向角，m为无人机总体重量。M为整机所受外合力矩，与旋翼机角速率及副翼、升降、方向舵控制量相关非线性方程[2-3]。

上述模型适用于绝大多数机体一体飞行器，细分旋翼机在不同状态下姿态模型需将旋翼飞行器视为自由刚体机体（除被动旋翼之外机体结构）和旋翼系统两部分组成气动系统。细分后非线性全量模型可完整描述旋翼机空间运动中空气动力与力矩作用及相互作用，但全量数学模型中各状态量及操纵量间非线性强，无法使用控制理论控制系统设计。成熟控制理论在线性化数学模型中控制方法研究与控制系统设计更简便。由于控制方式上旋翼机与固定翼飞行器一致，因此将旋翼机非线性运动方程线性化处理尤为必要。

本文根据线性化处理方法，采用“小偏差”线性方法，对无人旋翼机非线性全量运动方程线性化处理。无人旋翼机在某个平衡点保持其受合外力及合外力矩为0，此时线速度保持稳定，做无角运动。当旋翼机受外界干扰或施加操纵量情况下，此时所受合外力及合外力矩产生较小变化，表示为：

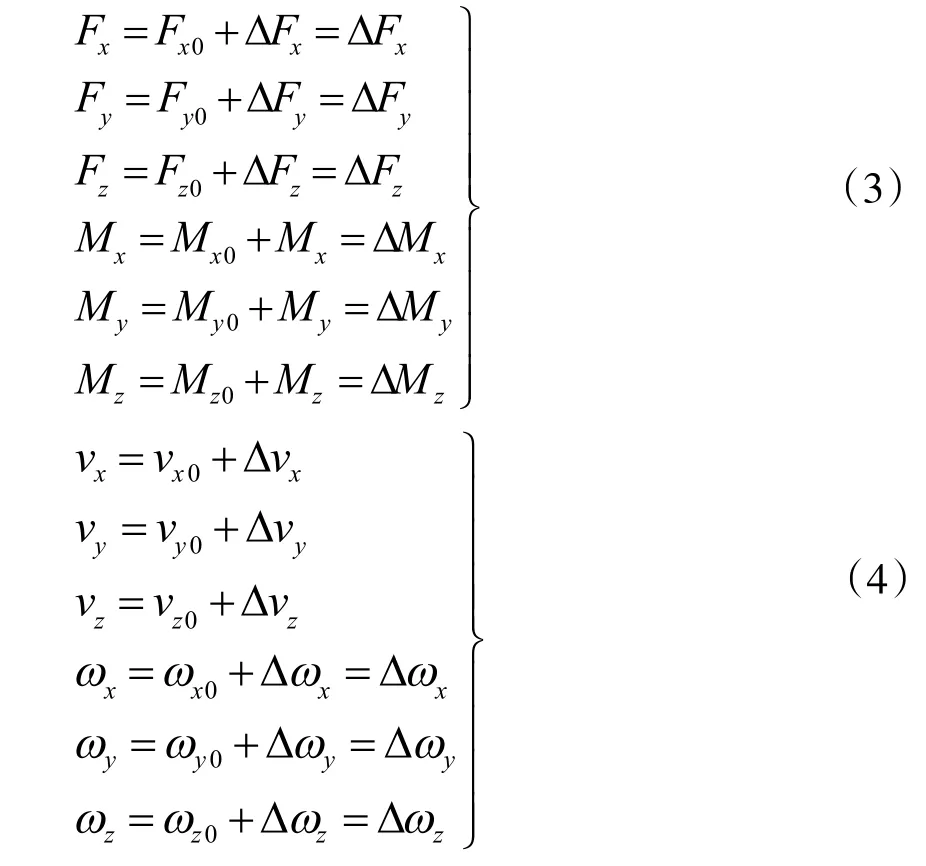
式中 Fx0、Fy0、Fz0及 Mx0、My0、Mz0分别为旋翼机在基准运动下所受合外力及合外力矩。在外在干扰下及外加操纵作用下，旋翼机线速度和角速度Δvx、Δvy、Δvz、Δωx、Δωy、Δωz也发生变化。其线速度和角速度与外加操纵变化Δδp、Δδe、Δδa、Δδr均有关系，采用偏导形式，则ΔFx表示为：

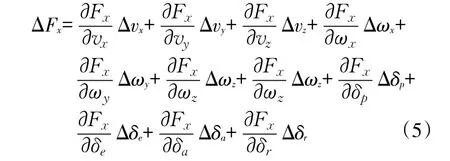
将（3）～（5）代入（1）、（2）中，整理得到旋翼机线性小偏差线性运动方程（忽略高阶小偏差增量）为：

式（6）中A，B分别为各方向合外力及合外力矩对飞行状态机操作输入偏导数矩阵。A矩阵中元素表示在基准状态下由于飞行状态变化导致力和力矩变化；B矩阵中元素表示在基准状态下操纵输入量导致力和力矩变化，具体参数不再赘述[1-3]。

由全量模型得出，在纵向通道内各状态变化及高度和前进速度由两个操纵组合控制实现。横侧向通道及航向通道气动模型结构与普通无人机类似。按“小偏差”线性方程分析，在控制率设计中，不计次要因素，对控制效果影响较小且简化控制率设计，简化Matlab仿真实验过程，有助于仿真试验和实际旋翼机姿态控制设计。

2 模糊PID姿态控制器设计

2.1 姿态系统结构

姿态控制系统作用是利用下一时刻目标姿态角与当前姿态角差生成下一状态时目标角速率指令，使旋翼机在指定角速率下达下一时刻目标姿态角。

采用双闭环结构应用于本文研究旋翼机姿态控制系统。双闭环结构中，外环回路中由姿态角动态逆控制得下一时刻目标角速率，而扩张观测器与滑模控制结合复合控制策略应用于内环回路实现旋翼机角速率精准控制，整体控制系统结构见图2。

外环控制主要作用是将目标姿态角与当前姿态角作差生成目标角速率，使旋翼机在给定角速率下能够快速达到目标姿态角。本文外环控制中所说动态逆控制是指采用代数求逆方法抵消系统一部分非线性，再选择合适输入量，得到期望动态模型。应用动态逆控制思路是动态逆控制不需复杂增益调度，对线性精准模型被控对象非线性部分完全补偿。

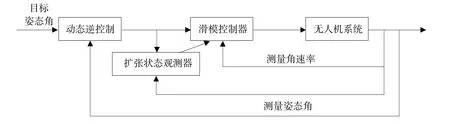
图2 旋翼机双闭环姿态控制系统结构Fig.2 Frameof UAV attitude-control system

从（1）式中得知，姿态角与角速率相关方程为非线性。式（1）中，将角速率作为姿态系统输入，式（1）状态方程可改写为式（7）。

式中，g（x）为非线性控制分布函数。由于姿态角特性可知φ，，故在飞行状态下|g(x)≠0|因此非线性控制分布函数g（x）可逆，故由式（7）可得

从式（9）可知，v为系统控制量，带入设计特定量，最终可得动态误差为0。

内环控制采用滑模变结构鲁棒控制方法与扩张观测器观测模型非线性项相结合复合控制策略控制结构如图3所示[3-7]。

非线性滑模控制器中，s为空间滑模面，设x˜为状态量跟踪误差。在空间滑模面s外满足≤-η|s|滑模条件。选择控制量为Uˆ=-f（ˆx）+x˙d-λx˜，此时可得滑模面为：

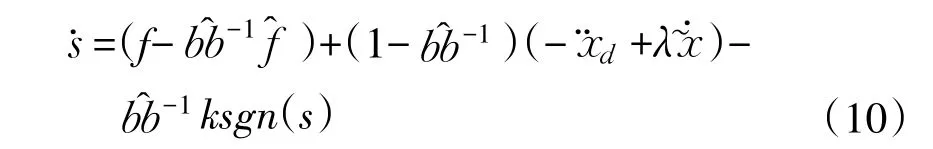
而切换控制增益 k满足 k≥BF+ηB+（B-1）（ fˆ-x¨d+ λx˜˙）。本次仿真中滑模控制器参数 λ=2.78，η=0.15，F=0.5fˆ，B=1.15

从（10）式与控制增益k满足条件可见，内环控制系统中滑模变结构控制在计算控制增益不确定性时降低控制连续性，但旋翼机控制中瞬时控制切换无法实现，激发旋翼机模型中高频未建模部分，为减免这种情况，文中使用边界层饱和函数消除颤振，使用饱和函数sat（s/φ）。

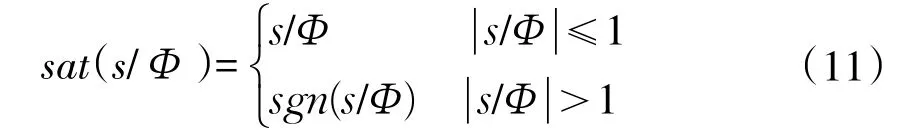
式（11）中，Φ为滑动平面边界厚度，该值越大，滑动平面边界越宽，本次仿真Φ=0.24。在边界层内系统状态轨迹连续，减小颤振。采用边界层饱和函数方法放弃部分跟踪性能[5-10]。

而内环控制中采用扩张观测器方法是估计非线性项f（x），可解决旋翼机建模困难，实现观测扰动项并保证控制器在控制系数稳定情况下保持较强适应性。对于旋翼机角速率一阶系统扩张状态观测器如式（12）所示[8-9]。

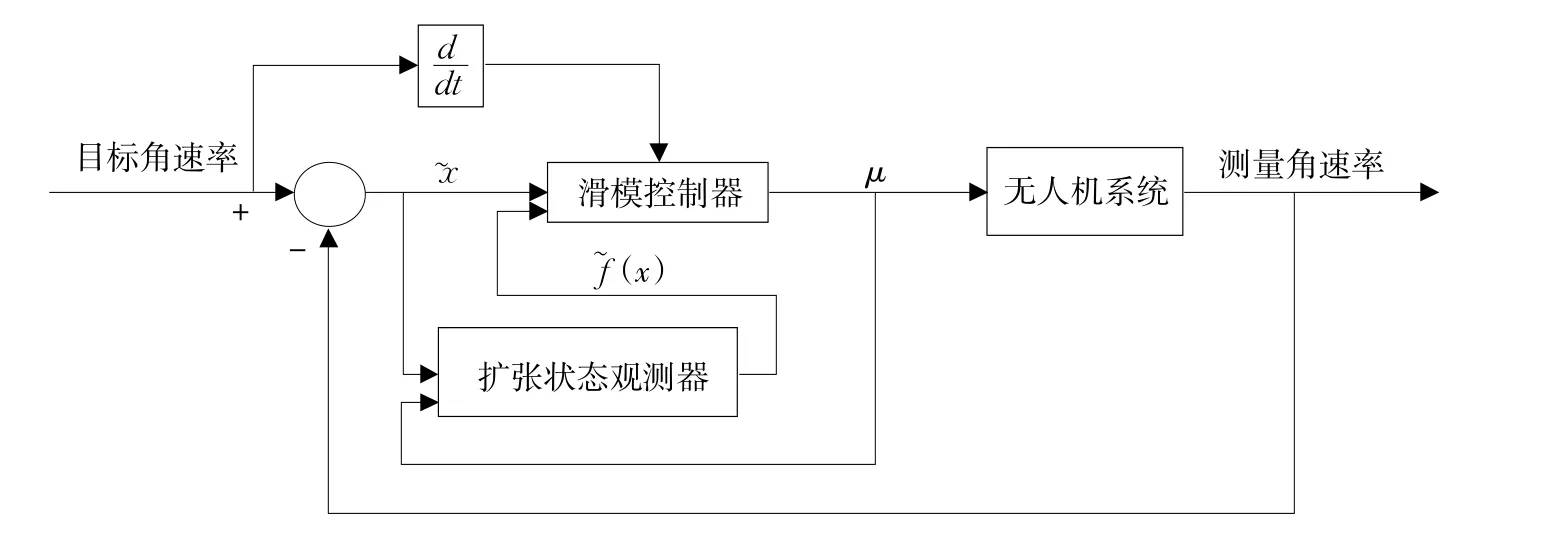
图3 角速率控制结构Fig.3 Structureof angular ratecontroller

滑模变结构鲁棒控制解决模型参数不确定性问题，扩张观测器解决模型结构不精确性问题，两者互为补充，最终解决角速率闭环系统控制稳定性和一致性问题。

2.2 经典PID控制与模糊控制

经典PID控制器是具有良好性能线性控制系统，通过对比目标状态与现实状态偏差比例（P）、积分（I）、微分（D）控制实现对系统准确控制。PID控制中，比例控制（P）主要调整系统响应时间，用于快速减小偏差，但如果比例系数不当容易引发超调，导致飞行器姿态调节过于灵敏；积分控制（I）主要用于消除静差，提高控制精度，但参数不当影响系统响应速度；微分控制（D）主要用于当系统进入较大偏差之前过渡至下一个调节周期，加快响应速度，减少系统震荡时间[12]。

在飞行器系统中，经典PID控制器将预先设定目标姿态角与当前角度传感器（陀螺仪，加速度计等）输入姿态角之间偏差，针对飞行器现状及飞行器下个瞬间预测瞬时状态，输出控制量调整飞行器姿态状态。根据经典PID控制定义，Matlab Simulink仿真，如图4所示。

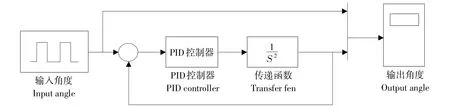
图4 经典PID控制Matlab Simulink仿真Fig.4 Conventional PID simulation diagram using Maltab Simulink

模糊控制是模拟人类思维方式控制理论，关键是模糊控制规则表。根据以往经验和反复调试设计优良模糊规则表，设计出性能较好模糊控制器。

设计模糊控制器控制规则根据Kp，Ki，Kd及e、ec关系，整定基本原则，结合研究人员经验，建立模糊控制规则表。模糊控制器输入与输出变量之间论域，一般选择误差e和误差变化率ec及控制量论域均大于或等于6。

2.3 模糊PID姿态控制器结构

模糊PID姿态控制器将模糊控制器与经典PID控制结合并将双闭环姿态控制系统作为被控对象，通过不断检测姿态角误差e和误差变化率ec，根据模糊控制规则在线实时对PID控制器Kp，Ki，Kd3个参数整定，使旋翼机具有良好动态与静态性能。控制结构见图5。

模糊PID控制器工作原理是3个双输入—单输出模糊控制器，在运行过程中不断把被控对象即上文提到姿态控制系统输出值与给定值比较，得偏差e和偏差率ec计算，求出PID控制器3个参数增量 ΔKp，ΔKi，ΔKd，在初始参数值 Kp0，Ki0，Kd0基础上整定。

本次仿真中偏差e和偏差率ec论域为{-3，-2，-1，0，1，2，3}，将基本论域划分为7个模糊子集：{负大，负中，负小，零，正小，正中，正大}分别对应字母缩写为（NB，NM，NS，ZO，PS，PM，PB）。模糊PID控制器其控制策略核心为模糊控制，而模糊规则是模糊控制器核心，模糊规则决定控制器性能。

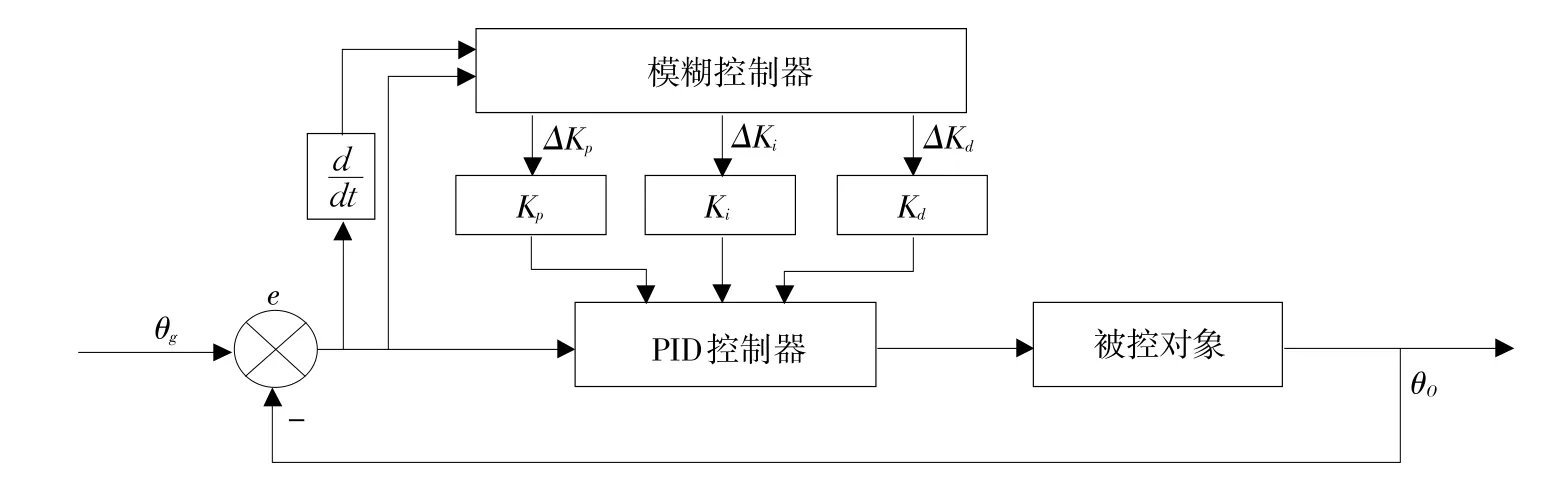
图5 模糊PID控制器Fig.5 Fuzzy PID controller

①当误差值e比较大且误差率ec较小时，为提高系统反应速度，Kp应选用较大值，为防止超调过大，Ki，Kd取较小值；

②当误差值e和误差变化率ec中等大小时，Kp，Ki取适中值，Kd取较大值；

③当误差值e较小时，Kp取较大值且为减小静差，增大Ki值，而Kd随误差变化率ec变化[11-17]。

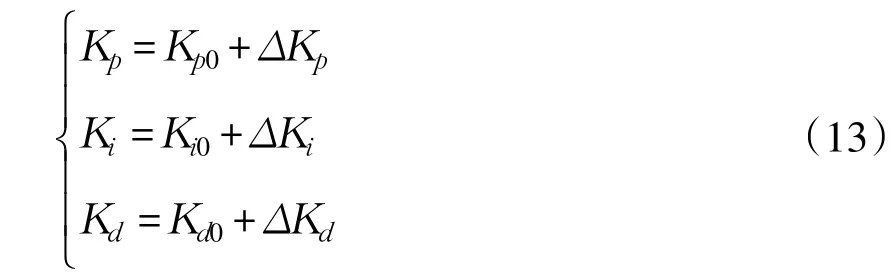
由上述描述得模糊规则表1。

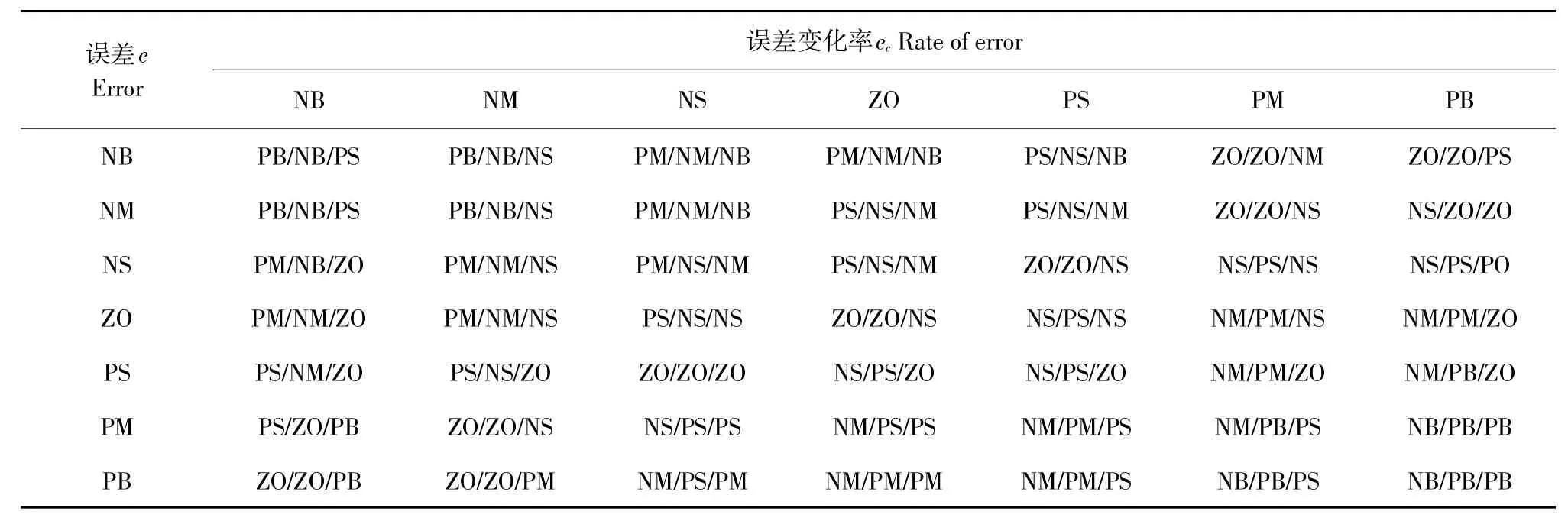
表1 Kp，Ki，Kd 模糊规则Table1 Fuzzy ruletable

3 仿真结果与分析

对比并仿真研究模糊PID控制器与经典PID控制器对系统阶跃信号响应，外加阶跃激励信号，研究其对指令信号收敛性与收敛速度。仿真结果见图6。

设置运动轨迹为画圆运动，外环姿态角控制回路在给定目标俯仰角和滚转角情况使用MATLAB仿真，观测仿真姿态角与目标角之间误差。平飞阶段，在指令滚转角为+18°时，目标滚转角与仿真滚转角对比如图7所示。

平飞阶段，在指令滚转角为+0.4°时，目标俯仰角与仿真俯仰角对比如图8所示。

稳定画圆飞行后滚转角、俯仰角最大、最小角度以及与目标角误差如表2所示。

仿真俯仰角速率如图9所示。

仿真滚转角速率如图10所示。

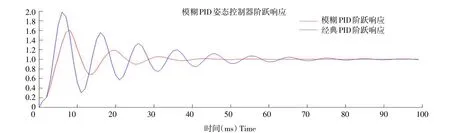
图6 模糊PID与传统PID仿真比较Fig.6 Simulation comparison between fuzzy PID and traditional PID

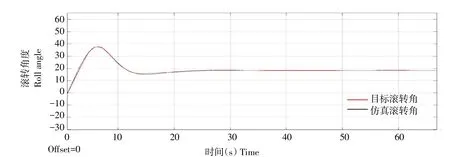
图7 目标滚转角与仿真滚转角对比Fig.7 Comparison between target roll angleand simulation roll angle

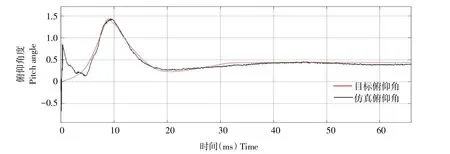
图8 目标俯仰角与仿真俯仰角对比Fig.8 Comparison between target pitch angleand simulation roll angle

表2 滚转、俯仰角与目标角对比表Table2 Comparison between roll angleor pitch angleand target angle

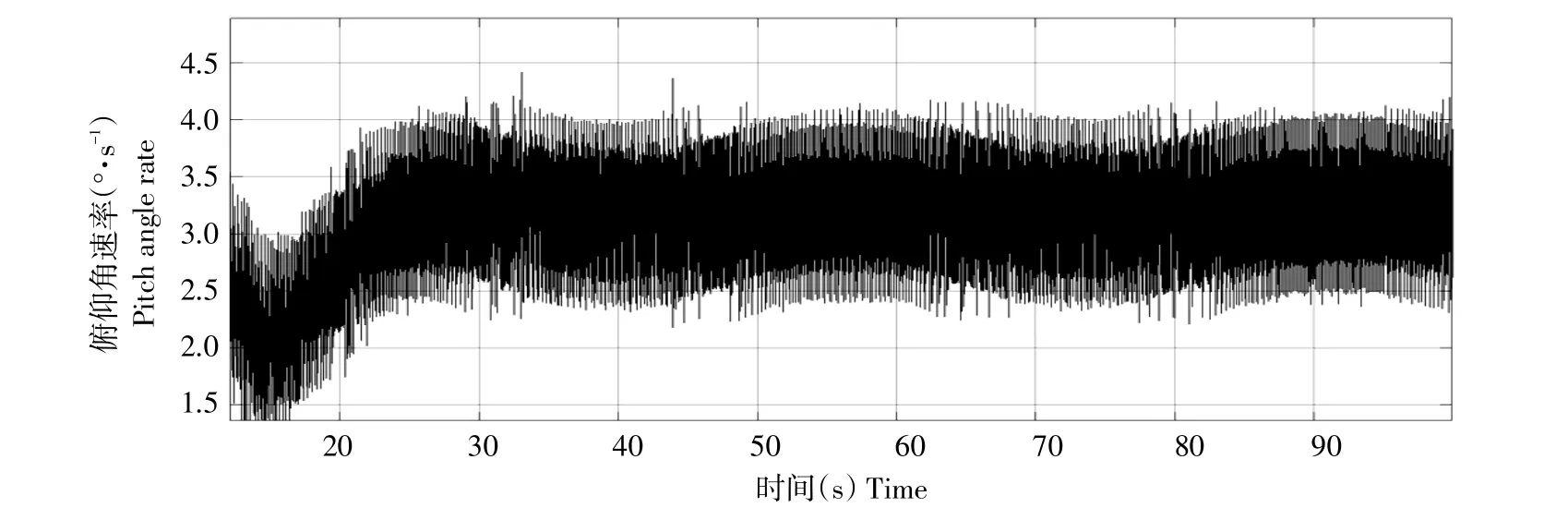
图9 仿真俯仰角速率Fig.9 Simulation of pitch anglerate

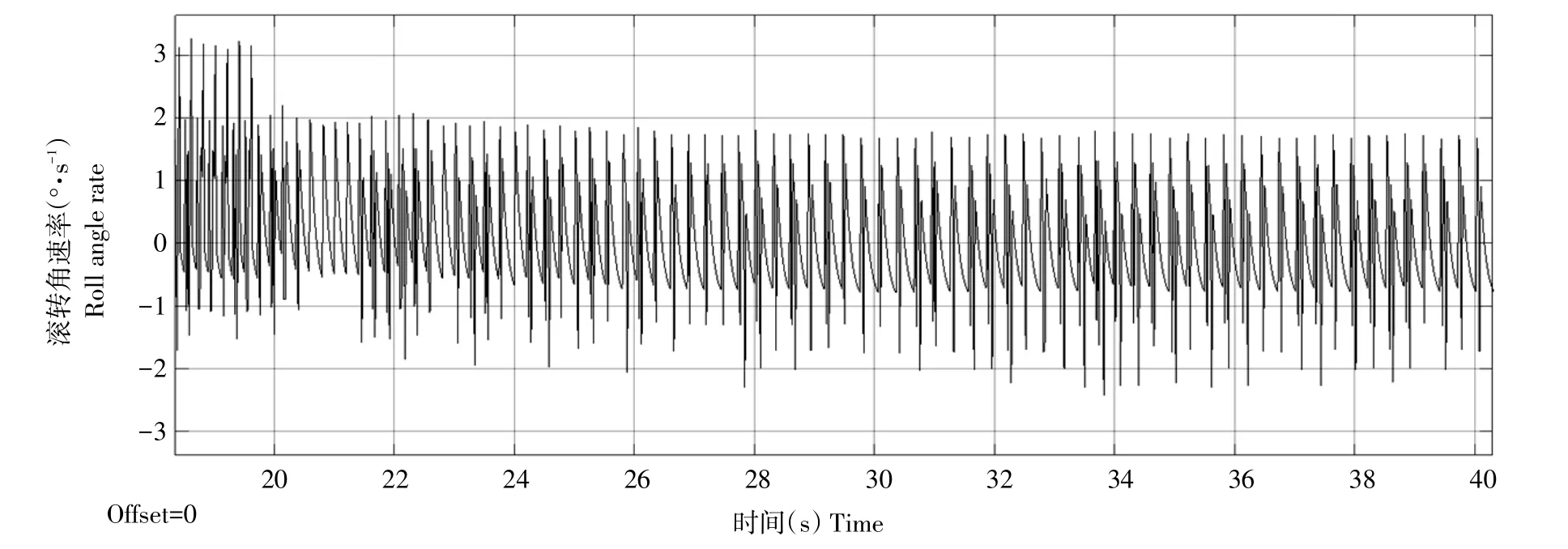
图10 仿真滚转角速率Fig.10 Simulation of roll anglerate

稳定平飞后，仿真滚转角速率、俯仰角速率最大与最小值如表3所示。

仿真结果显示，在系统阶跃响应下模糊PID控制器相较经典PID收敛时间减少0.04 s，而在给定目标角情况下滚转角和俯仰角误差在0.01°与0.05°上下。因此，在较大变化和存在扰动情况下，模糊PID控制性能优于经典PID控制。

从系统对于阶跃信号响应特性中可知，姿态控制系统中模糊PID不仅拥有经典PID控制高精度，计算量小、易实现优点，还具有超调小，动态响应快等优点。通过仿真也证明本文研究模糊PID姿态控制系统能够满足旋翼机在仿真飞行中稳定控制姿态要求，提高姿态控制速度和抗干扰性。

表3 稳定平飞后，仿真滚转角速率、俯仰角速率对比Table3 After steady flight,simulation of roll anglerateand pitch anglerate (°·s-1)

4 飞行测试与分析

本文采用单叶桨长600 mm，机身长度450 mm，机身重量1 000 g小型自旋翼航模机作为姿态角实际试验试飞机型。试飞样机体如图11所示。

起飞爬升与降落阶段采取人工遥控控制，进入平飞状态时切换到自动飞行模式。传感器记录滚转角与俯仰角数据如图12～13所示。由图12～13可知，试验机实际滚转角、俯仰角与指定目标角跟随性良好，表示旋翼机在平飞阶段可较好根据目标指令完成平稳飞行。在瞬间切换指令角度时，实际飞行角度有短时波动，跟随性有待提高。

图11 自转旋翼机试验机Fig.11 Unmanned autogyro

图12 指定滚转角与实际滚转角对比Fig.12 Comparison between target roll angleand real roll angle

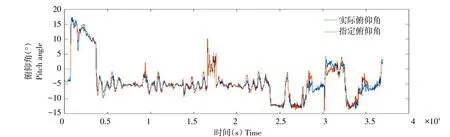
图13 指定俯仰角与实际俯仰角对比Fig.13 Comparison between target pitch angleand real pitch angle

5 讨论与结论

通过旋翼机姿态运动动力学模型与气动学模型分析，采用“小偏差”线性方法，对无人旋翼机非线性全量运动方程线性化处理。在纵向通道内，各状态变化及高度和前进速度由两个操纵组合控制实现，横侧向通道及航向通道气动模型结构类似普通无人机。在姿态控制设计时，根据其模型与以往经验采用双闭环复合控制策略。在双闭环控制策略中，外环姿态使用动态逆控制生成目标角速率，内环角速率控制使用滑模变结构控制与扩张状态观测器结合控制策略。将模糊控制与PID控制结合并应用于双闭环符合控制策略，可提高飞行控制中参数调整与动态响应性。

MATLAB仿真与实际飞行试验发现，经典PID控制器在控制旋翼机姿态控制上动态响应慢，参数调整困难；模糊PID姿态控制器具有控制灵活、鲁棒性好且适应性强优点，可根据输入偏差与偏差量实时调节控制参数，增强姿态控制稳定性，达到仿真中滚转角、俯仰角目标角要求。将该设计应用到实际旋翼机控制系统中，可在不改变原有硬件条件下增强姿态控制稳定性，在实际飞行中，平飞阶段姿态控制可较好完成自动飞行指令要求。

[1] 章卫国,杨向忠.模糊控制理论与应用[M].西安:西北工业大学出版社,2000.

[2] 陈健.无人直升机飞行控制技术研究[D].南京:南京航空航天大学,2008.

[3] 吴森堂,费玉华.飞行控制系统[M].北京:北京航空航天大学出版社,2005．

[4]刘焕晔.小型四旋翼飞行器飞行控制系统研究与设计[D].上海:上海交通大学,2011.

[5] 王俊超,李建波．机翼对自转旋翼机纵向稳定性的影响[J].航空学报,2014,35(1):151-160．

[6] 田卫军,李郁,何扣芳,等.四旋翼飞行器结构设计与模态分析[J].制造自动化,2014,36(2):37-41.

[7] 王俊超,李建波.自转旋翼/机翼组合构型飞行器飞行动力学特性[J]．南京航空航天大学学报,2011,43(3):399-450．

[8] 张兴文,陈铭.无人机姿态控制系统设计及仿真[J].计算机仿真,2016,33(7):158-161.

[9] 张鹏,张金鹏.变结构控制的抖振问题研究[J].航空兵器,2013,4(2):9-13.

[10] 段凤阳,陈鹏,郝爽.无人机姿态控制器设计与仿真[J].计算机测量与控制,2015,23(5):1571-1574.

[11] 林清,蔡志浩,闫坤.升降舵辅助操纵的自转旋翼机自适应姿态控制[J].航空学报,2016,37(9):2820-2832.

[12] 陈淼,王道波,盛守照.基于虚拟参考反馈的无人旋翼机姿态控制[J].南昌航天航空大学学报,2011,25(2):27-32.

[13] 陈鹏,段凤阳,张庆杰,等.基于模糊PID的无人机姿态控制器设计[J].弹箭与制导学报,2015,35(1):9-11,18.

[14] 刘斌,马晓平,王和平,等.小型电动无人机总体参数设计方法研究[J].西北工业大学学报,2005,23(3):396-400.

[15] 刘金琨.先进PID控制MATLAB仿真[M].北京:电子工业出版社,2011.

[16] 都基焱,张振.十字翼布局无人机半实物仿真系统设计[J].现代电子技术,2014,37(5):18-20.

[17] Naphon P,Wongwises S,Wiriyasart S.Application of two-phase vapor chamber technique for hard disk drive cooling of PCs[J].International Communications in Heat and Mass Transfer,2013,40(1):32-35.