数学教学中的哲学味
——以“因数与倍数”教学为例
□荀步章
儿童是天生的哲学家。当代哲学家周国平说:“哲学不具备简单意义的实用性,它是无形、无限与无定。如果把科学比作一片广袤的大地,那么,哲学就是一片无限的天空。”如何培养小学生的哲学数学思考意识,引发他们追问 “从哪里来” “怎样去找”“有何特征” “到哪里去”,数学教学应该有自己的回答,在反复追问与辩证理解中发展学生数学的综合素养。笔者通过 “因数与倍数”一课想表达一点哲学数学的思考。
一、从哪里来
师:数学要研究 “数”,一年级开始,我们就学习自然数,自然数包括哪些数?
生: 0, 1, 2, 3, 4……
师:今天研究的数指不是0的自然数,叫非0自然数。
1.除法运算
师:数学要研究两个数之间的关系,老师用两个自然数做了几道除法算式。
依次出示: 12÷2=6 8÷3=2……2 36÷9=4 19÷7=2……5 15÷15=1 1÷2=0.5
师:仔细观察思考,谁来把这些算式分类?
学生尝试分类:
第一类: 12÷2=6 36÷9=4 15÷15=1
第二类:8÷3=2……2 19÷7=2……5
第三类:1÷2=0.5
师:怎样想的?
生:第一类算式中的每一个数都是自然数,第二类算式中都有余数,第三类算式中有小数。
师:特别研究第一类算式,像这样,被除数、除数和商都是自然数,没有余数。比如,12÷2=6,我们就可以说12是2的倍数,2是12的因数。也可以说,12是6的倍数,6是12的因数。
师:谁来说一说36÷9=4这道算式中因数与倍数的关系。
生:36是9的倍数,9是36的因数,36是4的倍数,4是36的因数。
生:15是15的倍数,15是15的因数。15是1的倍数,1是15的因数。
师:谁愿意出一道除法算式,让其他同学说一说。
……
【反思】从一年级认识的一个自然数出发,学生很熟悉,接着,用两个非零自然数做除法运算,寻找符合整除的算式,并聚焦这一类算式,被除数、除数和商都是整数,没有余数,发现两个数之间的因数与倍数关系,完全符合数论基础。因数与倍数是相互依存的辩证关系,有因数就有倍数,有倍数就有因数,中间用 “与”连接。因数与倍数从哪里来,从整除运算中来。
2.图形表示
师:用小方块拼长方形,一排摆6个,摆2排,一共用了多少个小方块,怎么算?
生: 6×2=12。
师:这道乘法算式里有因数与倍数关系吗?
生:6和2都是12的因数,12是6和2的倍数。
师:这幅点子图,怎么算?
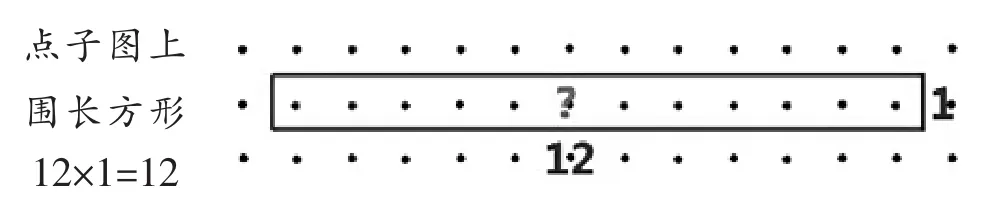
生: 12×1=12。
师:谁来说一说,这道乘法算式中有因数与倍数关系吗?
生:12和1都是12的因数,12是12和1的倍数。
师:这是一幅线段图,怎样求乙?
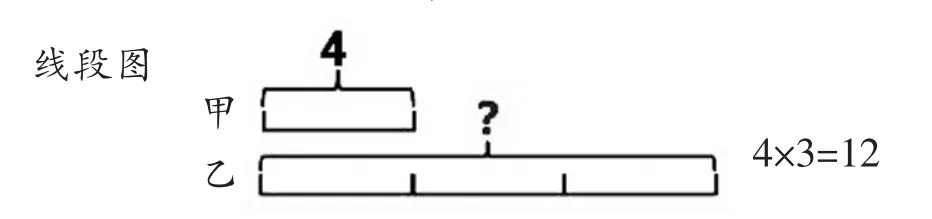
生: 4×3=12。
师:谁来说一说,这道乘法算式中有因数与倍数关系吗?
生:4和3都是12的因数,12是4和3的倍数。
师:这些图形中的数可以选0吗?
生:不能,因为选0就不能构成图形了。
师:这也说明了因数与倍数研究的是非0自然数。因数与倍数是从哪里来的?从乘法、除法运算中来,从图形的表示中来。
【反思】亚里士多德说: “哲学是一切学问中最为自由的,因为它仅仅为了自身而存在。”因数与倍数是一种依存关系,通过整除运算让学生理解还不完整,借助图形表示,在乘法运算中同样存在因数与倍数的关系。跳出除法算式,建构乘法意义的因数与倍数。这一组图形数形结合,使学生进一步理解因数与倍数的意义。
二、怎样去找
1.找12的因数
师:老师找了几份研究单,一起来分享一下。

生:通过除法来寻找12的所有因数,从1开始,12÷1=12, 12÷2=6, 12÷3=4, 12 的 因 数 有1, 2, 3, 4, 6, 12。
师:朱同学找的非常好,掌声表扬。他用了什么好方法?
生:按顺序找。
生:按自然从小到大的顺序。

生:用乘法算式来找的,1×12=12,2×6=12, 3×4=12, 12 的因数有 1,12,2,6, 3,4。
师:蒋同学找的也非常好,但她写的因数没有按自然数顺序。
师: (电脑演示)第一步怎么找?用乘法或除法找。第二步怎么算?乘法先算1×12=12、2×6=12、3×4=12; 除法算 12÷1=12、 12÷2=6、 12÷3=4。 不论乘法还是除法都需要有序一一列举。第三步怎么写?先写1和12,一前一后,再写2和6,一前一后,最后写3和4,这样成对写很快,而且有序。
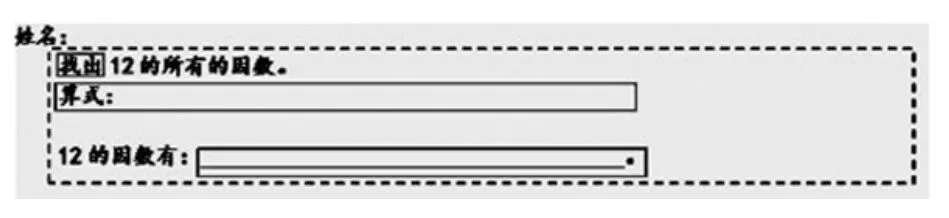
怎么找? 乘法 除法
怎么算?
1×12=12 12÷1=12
2×6=12 12÷2=6
3×4=12 12÷3=4
怎么写? 12的因数有1,2,3,4,6,12.
【反思】给学生问题挑战,尝试找出12的所有因数。学生受起始学习影响,部分学生用除法运算去找,还有学生用乘法算式有序找到12的所有因数,在具体写出12的所有因数时,注意一前一后成对有序写,学生感受到数学思考的理性与思辨。
2.分组找15、36、16的所有因数
师:第一组找15的所有因数,第二组找36的所有因数,第三组找16的所有因数。
先独立完成,再与同学交流。

生: 用乘法找,1×15=15,3×5=15,15的因数有1,3,5,15。在数直线上圈出来。

生: 用乘法找, 1×36=36, 2×18=36, 3×12=36, 4×9=36, 6×6=36, 36的因数有1, 2, 3, 4, 6, 9, 12, 18, 36。这里的6有2次,为了不重复,写一个就行了,并在数直线上圈出来。
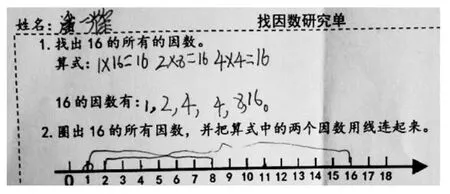
生: 用乘法找, 1×16=16, 2×8=16, 4×4=16,16的因数有1,2,4,4,8,16。这里的4也有2个,我多写了一次,应该去掉一个4。
师:这三位同学都用乘法有序找了一个数的因数。
【反思】在全班找12的所有因数的基础上,放手让学生自主探索一个数的所有因数,全班分3个小组,每人完成一个数,强化寻找的过程,按自然数顺序一一列举,强调相同因数只要写一个,借助数形结合,把每个数的因数成对在数直线上表示出来,与写因数的过程一一对应。
3.分组找2、3、5的倍数
师:带着找一个数因数的方法,试着找一个数的倍数。第一组找2的倍数,第二组找3的倍数,第三组找5的倍数。
师:有什么问题吗?
生:一个数的倍数有无数个,怎么写?
师:一般写出前6个,加上省略号。
学生一一找2、3、5的倍数。全班交流反馈。

生:用乘法算式一一列举,1×2=2,2×2=4,3×2=6,等等,2的倍数有2,4,6,8,10,12……

生:用乘法算式一一列举,1×3=3,2×3=6,3×3=9,等等,3的倍数有3,6,9,12,15,18……

生:用乘法算式一一列举,1×5=5,2×5=10,3×5=15, 等等, 5的倍数有5,10, 15, 20, 25, 30……
师:怎样去找一个数的因数呢?
生:用自然数1、2、3……与它相乘,很快就能找到一个数的倍数。
【反思】找一个数的倍数学生很容易,以找一个数因数为基础,用乘法计算,从自然数1开始,依次与这个数相乘,口算思考都简单。这里主要解决写多少、怎么写的问题。学生开始就有疑惑,一个数的倍数无限个,怎么办呢?按规定写出6个,加上省略号,表示无限多。
三、有何特征
师:电脑呈现,回顾找一个数因数的过程。
15的因数有1,3,5,15
36的因数有1, 2, 3, 4, 6, 9, 12, 18, 36
16的因数有1,2,4,8,16
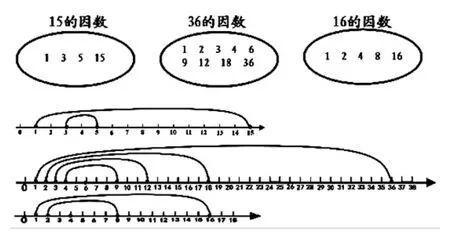
师:仔细观察每一个数的因数,有何特征?
生:一个数的因数中最小是1。
生:一个数的因数中最大的是本身。
师:15有几个因数?36和16呢?
生:4个、9个和5个。
师:一个数的因数个数是有限的还是无限的?
生:有限的。
师:再一起回顾找一个数的倍数过程。
2的倍数有2,4,6,8, 10,12……
3的倍数有3,6,9,12,15,18……
5的倍数有5,10,15,20,25,30……
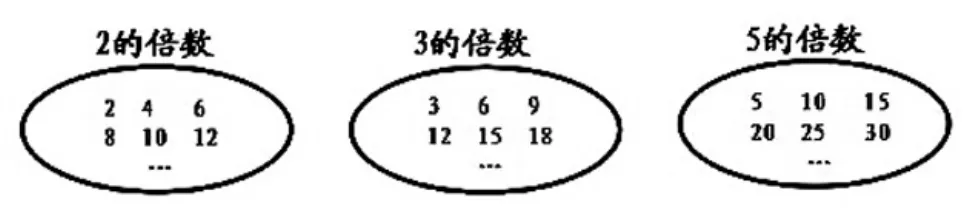
师:仔细观察一个数的倍数,有何特征?
生:一个数的倍数中最小的是它本身。
生:一个数的倍数没有最大的,因为自然数有无数个。
生:一个数的倍数个数是无限的。
师:思考一下,找一个数的因数和倍数有什么相同点和不同点?
生:相同之处是因数和倍数都是从乘法、除法的角度去寻找,有序地找,因数、倍数中都有本身。
生:不同之处,一个是从本身开始向内找,有限个;一个是从本身向外找,无限个。

课件呈现:
师:我们研究了因数与倍数,表示两个数的相互依存关系。一是从哪里来?整数乘法、除法运算和图形表示中都可以找到因数与倍数。二是怎样去找?用乘法或除法去找,有序找,成对找。三是有何特征?一个数的因数个数是有限的,在1到它本身之间;一个数的倍数是无限的,从它本身开始,没有最大的。还有一个问题需要思考,就是 “到哪里去”。
【反思】学生通过探索学会了找一个数的因数和倍数,回顾反思,列举15、36、16的所有因数,发现一个数的因数最小的是1,最大的是它本身,个数是有限的,还相机呈现维恩图的表示方法、数直线的表示方法,多元表征形象理解。再回顾寻找2、3、5的倍数过程,发现一个数的倍数最小是它本身,最大的不存在,个数是无限的。辩证思考理解,找一个数的因数由本身向内寻找,而找一个数的倍数是由本身向外寻找。
四、到哪里去
1.生活中
师:生活中有关于求一个数的因数与倍数的问题吗?
问题一:乘坐小船每人应付4元,填写表格。

师:怎么填?
生: 12, 16, 20, 24……
师:这是求一个数的倍数,还是因数?
生:求一个数的倍数。
问题二:24个学生表演团体操,填写表格。

师:怎么填?
生: 8, 6, 4, 3, 2, 1。
师:这是求?
生:求一个数的因数。
2.数学中
师:数学中求一个数的因数还有研究,老师想给大家介绍一个特别的数6。6的因数有哪些?
生:1, 2,3, 6。
师:除去6本身,把剩下的因数相加。你发现了什么?
生:结果还是等于6。
师:这样的数很特别,数学家们将具有这一特点的数称之为完美数。6就是第一个完美数。想知道第二个完美数是多少吗?
生:想!
师:透露一下,比25大,比30小。
组内分工合作,看看哪一小组最先找出第二个完美数!
学生很快找出了第二个完美数28。
师:其实,人们对于完美数的探索兴趣是永无止境的,找到了第二个完美数,人们就开始寻找第三个、第四个,看……

师:想一下,要找出这些完美数来,有什么感觉?
生:我觉得太了不起了!
生:这需要付出多大的艰辛呀!
师:究竟是什么力量,吸引着一代又一代数学家为此付出毕生的心血呢?
生:是完美数本身。
生:是他们对于数学的热爱。
生:对于数的好奇心。
师:数学王子高斯说过,数学是自然科学的皇后,数论则是数学的皇冠。今天时间有限,我们只看到了皇冠上一粒小小的珠子,但只要我们沿着这条路走下去,一定会收获很多东西。同学们,努力吧!未来属于你们!
【反思】学生学完因数与倍数后,心中会有疑惑,因数与倍数有什么用?这里从两个方面进行延伸,一是从生活中的问题入手,如坐船付钱问题是求一个数的倍数,团体操表演问题是求一个数的因数;二是从数学本身出发,找出一个数的因数,除去本身,把剩下的数相加,若等于它本身,这个数就是完美数,进行数学探究精神的教育,引发学生热爱数学的兴趣。
【整课反思】本课想体现一点哲学数学的味道,通过 “为什么、是什么、怎么办”的追问,让学生整体理解因数与倍数的相互依存关系。为什么要研究?怎么研究?还有什么?除此之外,我们还想体现一点其他味道:
一是 “数学味”。从例题改编出来,强调直观,从非0自然数引入,探索整除算式,数形结合思考,一一有序列举策略等,想呈现一种数学味。
二是 “儿童味”。让学生在个人独立探索一个数的因数与倍数,小组交流、全班展示的过程中发现一个数因数与倍数的特征,让儿童自主生长发展,促进学生学习能力的提升。
三是 “问题味”。杜威说: “教育中永远成功的教学方法是,给学生一些事情去做,不是给他们一些东西去学。”学生探究找12的所有因数,在思考与交流中提升,对比发现一个数因数与倍数特征的异同,追寻数学问题横纵联系。
四是文化味。因数与倍数是同时存在的,谁也离不开谁。除法算式关系如何表示?乘法算式关系如何表示?如何求出一个数因数与倍数,由本身向内、由本身向外寻找的方法,慢慢体会两者的关系,满足不同学生学习差异需求。
正如俞正强老师在 《人民教育》2017年第10期开篇一文所说, “干所有的事情,都要先明白我要干什么,上课亦是如此。”

