高中数学教学微探

□张希荣

高中数学题浩如烟海，想做完是不可能的，想通过做题压上考试题几乎是不可能的。那么，怎样才能学好高中数学，轻松得高分呢？笔者认为，关键是要把握高中数学各单元的本质属性，并不断地提高自己的数学学习能力。高中数学既有很多规律性的东西，更有很强的灵活性。要到达解题的灵活性，掌握高中数学各单元的规律性是关键问题。那么，怎样才能掌握高中数学各单元的规律性呢？笔者认为，那就是学生在学习高中数学的过程中要建立好自己的 “数学笔记”和 “错题本”，即 “资料库”，并利用好自己的“资料库”。

一、高中数学笔记

就高中数学某一单元来说， “数学笔记”就是记录研究过的、理解透彻的数学知识和常见的结论、运算数据等；就是记录代表很好的数学思想方法的经典问题和解法要点。

（1）记录常规的数学定义、定理和公式等。

（2）记录常见的结论。例如，学生在学习椭圆一节时，除了记录椭圆的定义、椭圆的标准方程、椭圆的几何性质和直线与椭圆位置关系以外，还要记录椭圆的焦半径公式、椭圆的通径公式以及如何判断点与椭圆的位置关系的式子等。

（3）记录常用的数据。我们经常用的数据记住就好了，不用每次考试都要计算。例如，从1到32的平方数，从1到6的立方数，2的常用对数和自然对数值等，在考试的时候可以直接运用，不用再去浪费时间推算。

（4）记录本单元常见的经典题型。要分门别类，整理、记录好经典的问题解法要点 （不需要过细，主要记录自己容易想不到的解题思路和最终答案），特别是一些通用解法和最简便解法。这些经典数学题可以是课堂上教师讲的，也可以是自己钻研的，只要是精彩的解题思想方法就要收录。

（5）记录本单元的易错点。例如，在学习 “椭圆”一节时，一道题给出一个点的坐标，我们经常需要设出直线方程的点斜式，这就说明我们默认了直线的斜率存在，那斜率不存在的情况我们考虑了吗？没有考虑的话，这道题解答的就不全面、不完美，就会扣分。

（6）记录一些运算的妙招和运算方法。高中生的运算求解能力是他们考试能否得到高分的重要因素，长期只重视解题思路，对于较为复杂的运算就退避三舍，会造成学生计算能力差，在计算时使用蛮力，得不到正确的答案。我们应该不断地总结运算方法，注意在运算过程中的妙招。

总的说来， “数学笔记”应该记录的东西可归纳成如下思维导图：

“数学笔记”不是一朝一夕就整理落实好的，就像每天写日记一样，长期积累下去才能有一套真正有用的 “数学笔记”。

许多学生因为懒惰，没有 “数学笔记”；也有的学生在教师的检查监督下才有 “数学笔记”，上课时教师在黑板上写什么他们就记录什么，眉毛胡子一把抓，里面有用的东西占的比例很小，这种 “数学笔记”根本没有用。

学生记录的 “数学笔记”应该是学生理解透彻的数学知识和常见的结论、好的解题思想方法，不是不会做的数学题。不会解的数学题不要记录在 “数学笔记”里，不会解的题，应该记在 “错题本”上。

二、错题本

目前，高中生在解题过程中普遍存在 “看错、算错、抄错、涂错和错觉”，即所谓 “五错”。怎么解决“五错”这个问题，一直困扰着教师和学生。笔者认为，要解决这个问题，除了在思想上提高认识，在审题上狠下功夫以外，最好的方法应该就是做好 “错题本”。

在整理 “错题本”时，首先要明确 “错题本”里面记录些什么的问题。就高中数学某次考试来说，记录好年月日和哪次考试中的哪一道题或者哪一天的作业题；记录的数学题应该是会做但是做错了，或者做的不完整，考虑不周全的试题；记录做考试题时出错的原因，记录好该试题的标准结论。

总的说来， “错题本”应该记录的东西可归纳为如下思维导图：

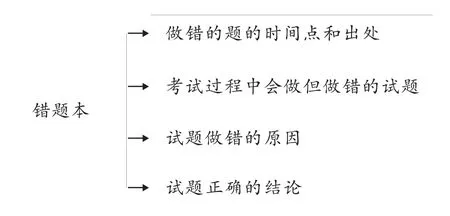
学生在迎接大型考试时，首先，应该利用好 “数学笔记”。重新推导和记忆要考查内容的数学基本知识和常见的结论，重新演练 “数学笔记”中的数学题的解题思想方法，重新记忆常见的数据，重新理解数学计算方法和运算经常用到的妙招。 “数学笔记”中记录的解决数学问题时规律性的东西，熟练地掌握这些规律性，才能灵活地解决数学难题；其次，要经常重新认识 “错题本”中的题，明白自己曾经是怎么做错的，牢记教训，把失误降到最低，努力达到 “零失误”。

总之， “数学笔记”和 “错题本”就是每个立志学好高中数学的学生应该建好的 “资料库”，想要用好这个 “资料库”，就要对 “数学笔记”和 “错题本”中记录的东西进行反复理解、反复练习和反复记忆，达到熟练运用、记忆犹新，做难题也就水到渠成了。

[1]吴陈兵．知识就是力量？——兼谈人的核心素养教育［J]．教学研究ResearchinTeaching．2016，（3）．

[2]吴元良．高中数学复习课教学中思维导图的应用探析［J]．中学课程辅导（教师通讯），2014，（11）．