教育资源抑或同伴效应？——学校因素对学生学业成就的影响分析

张文宏，韩 钰

(上海大学 社会学院，上海 200444)

一、引言

教育公平问题一直是教育学和社会学关注的热点问题，当前对我国教育公平问题的分析主要包括两个方面：首先是家庭背景导致的教育不平等，其次是学校间的教育质量不平等。对于家庭背景因素的影响，本文将不展开深入的讨论，本文旨在分析学校因素在教育不平等中的作用。根据美国著名教育经济学家Hanushek建立的经典教育生产函数模型*Hanushek, E. A., “The economics of schooling: production and efficiency in public schools”, in Journal of Economic Literature, Vol.3 (1986), p.1141-1177.，除家庭背景之外，学校在教师、经费上的投入将会对教育质量(成绩)产生影响。作为一个发展中国家，教育资源在我国仍属稀缺资源，在配置方面仍有很大的不均衡性，不同地区、不同学校之间所享受到的教育经费投入、教育基础设施、师资力量等仍有较大差异，对教育资源配置在学生学习成绩中的作用展开分析是十分必要的。

但是随着研究的深入，学者们也开始在原有的教育生产函数模型之外加入同伴关系的影响。根据社会心理学的研究成果，同辈群体是一个人成长发展的重要环境因素，尤其是在青少年时期，同辈群体的影响日趋重要，甚至有可能超过父母和教师的影响。在一些实证研究中，学者们也已经多方面证实了同伴关系对学生性格、心理和人际交往等方面的影响。在著名的科尔曼报告中，就开始将同伴的作用运用到分析学生的学习成绩中，随后也有一些学者展开了对这一问题的分析。但是在国内的相关研究中，针对同伴关系对学生学习成绩影响的研究还比较少，随着我国教育机会的不断扩大，学生结构越来越复杂，对这一问题的实证分析也逐渐提上日程。随着中国城市化的进程，传统的邻里关系发生了变化，邻里交往日渐减少，再加上我国长期实行独生子女政策的影响，目前处于青少年阶段的学生较少拥有社区和家庭同辈群体，学校同学成为他们接触最多、产生影响最大的同辈群体。

当前我国初中阶段基本上实行的是以“学区房”为基础的就近入学政策，高中阶段大多都是根据考试分数的择校入学政策。现实生活中，不管哪种入学政策，拥有较多教育资源的重点学校总是会吸引更多家庭背景较好或学习成绩较高的学生聚集，从而会出现一定程度的同质聚集效应。所以，在我国教育资源投入和同伴关系之间就具有一定的相关性，那么两种效应聚合在一起将会对学生的学习成绩产生什么样的影响？本文就旨在采用国际学生能力评估项目(PISA2015)中国四省市数据，以定量研究的方式分析学校因素中的教育资源和同伴关系对15周岁青少年学生学习成绩的影响。

二、文献述评与研究假设

对于教育投入即教育资源配置均衡问题的关注一直是国内学者研究的热点，但这些研究主要在于分析不同区域、不同学校之间资源配置的不均衡及由此带来的教育获得方面的不平等问题。他们往往把就读学校的质量作为重要的影响因素，认为重点学校通常集中了优秀的师资和生源，对儿童下一阶段教育机会的获得具有重要的影响*李忠路，邱泽奇：《家庭背景如何影响儿童学业成就?——义务教育阶段家庭社会经济地位影响差异分析》，《社会学研究》，2016年第4期。。对于学校内部教育资源配置与学生学习成绩之间关系的分析在国内则起步较晚。然而国外这方面的研究早在20世纪60年代《科尔曼报告》中就展开了讨论，之后国外学者围绕学校投入与学生成绩之间的关系问题展开了大量的研究。但是，根据Hanushek的总结，学校资源配置与学生成绩之间并不存在很强的相关性*Hanushek, E. A., “Assessing the effects of school resources on student performance: an update”, in Educational Evaluation & Policy Analysis, Vol.2 (1997), p.141-164.，但是这一因素在发展中国家中对学习成绩的影响却比发达国家更为明显。近几年来，国内学者对教育资源配置与学生成绩之间的关系也展开了实证研究，在这些研究中也陆续用到了最新的多层线性模型分析技术。在这些研究中，对学校教育资源在学生成绩中的作用，研究者们仍然存在争论。一些研究表明，学校的教育资源和学生学习成绩之间具有显著的正向关系*薛海平，王蓉：《我国义务教育公平研究——教育生产函数的视角》，《教育与经济》，2009年第3期；张启睿，边玉芳，王烨晖，等：《学校教育环境与资源对青少年学业成就的影响》，《教育研究》，2012年第8期。，但也有研究发现，二者之间几乎没有影响*胡咏梅，杜育红：《中国西部农村小学教育生产函数的实证研究》，《教育研究》，2009年第7期。。造成这种结果差异的原因在很大程度上是由于对教育资源的测量不一致导致的，所以有些研究就发现不同的教育资源对学生成绩的影响是不同的。李祥云、魏萍研究发现，教育经费、图书数量与学生各科成绩正相关，但高级教师比例对学生成绩没有影响，师生比例和生均固定资产对学生不同科目的成绩产生了不完全一致的影响*李祥云，魏萍：《学校资源配置对学生成绩的影响机制研究——基于对JX县小学问卷调查的实证分析》，《教师教育学报》，2014年第5期。。所以，学校教育资源对学生学习成绩的影响可能是不稳定的，如何从多个方面对学校教育资源进行测量，并尝试将各种不同的教育资源整合成一个综合性的指标进行分析是在今后的相关研究中需要注意的。另外，在分析过程中控制家庭背景因素也是必须的，因为家庭背景因素对学习成绩和所选学校的教育资源都有很大的影响，并且这种影响也会对教育资源在学习成绩中的作用产生干预。

近年来，随着我国教育机会的扩大，中小学布局的调整以及人口流动带来的学生流动的增加，学生的构成结构也发生了很大的变化，对学生同伴效应的研究也逐渐展开。对同伴效应的研究起源于社会互动论，起初这些研究也主要集中在分析同伴关系对学生性格、心理和人际交往等方面的影响。《科尔曼报告》之后，越来越多的研究将同伴效应运用到对学生学习成绩的分析中。在本文中我们说的同伴效应主要参照Zimmer & Toma的界定*Zimmer, R. W., & Toma, E. F. , ”Peer effects in private and public schools across countries”, in Journal of Policy Analysis & Management, Vol.1(2000), p.75-92.，主要是指学校、班级内学生构成的特点对学生个体成绩的影响。对于学生的同伴交往行为、特征则不是本文讨论的问题，所以对这方面的研究文献不再梳理。同伴效应对学生学习成绩的影响途径也是多种多样的，Sacerdote总结了几种常见的效应模型*Sacerdote, B., “Chapter 4 - peer effects in education: how might they work, how big are they and how much do we know thus far?”, in Handbook of the Economics of Education,Vol.4 (2011), p.249-277.，这些模型效应有些是相对立的。就班级结构而言，既有可能出现聚集效应(同质的同伴更有可能产生积极影响)，也有可能出现彩虹效应(班级的异质性对每个人都是好的)。

在具体的实证研究中，学者们对同伴效应的测量主要集中在以下两部分：(1)班级平均成绩和班级平均家庭背景，有些学者针对其中一方面进行分析，有些则对两方面均展开分析。Hanushek & Kain用年级同伴过去的平均考试成绩和标准差作为衡量同伴效应的指标*Hanushek, E. A., & Kain, J. F., “Does peer ability affect student achievement?”, in Journal of Applied Econometrics, Vol.5 (2003), p.527-544.；Mcewan用班级学生父母的平均受教育程度及其平方、家庭收入及其平方、本土学生的比例等作为衡量同伴效应的指标*Mcewan, P. J., “Peer effects on student achievement: evidence from Chile”, in Economics of Education Review, Vol.2 (2003), p.131-141.。国内学者或针对中国情况的相关研究也基本从以上两方面展开，但具体的实证研究并不多见。在一些研究中还加入了同伴性别构成和班级规模*杨钋：《同伴特征与初中学生成绩的多水平分析》，《北京大学教育评论》，2009年第4期。，同时也有一些学者将研究对象锁定在大学生群体，分析宿舍同伴效应*梁耀明，何勤英：《大学生学业成绩的宿舍同伴效应分析》，《教育与经济》，2017年第4期。。在为数不多的实证研究中，大都发现了类似的结论，即同伴水平的平均程度对个体具有正向作用，而异质程度具有负向作用，也就是说在中国班级结构更可能出现聚集效应而不是彩虹效应。

根据以上梳理，在很多研究中，研究者使用的班级成绩均值或标准差是与因变量中的学习成绩同期测量的，笔者认为这是很不合适的。首先，同期测量的数据在时间上并不具有先后性，很难分析真正的因果关系；其次，在中国，家庭背景对学生学习成绩的影响是巨大的，同时我国教育中又存在严重的学校阶层分割*吴愈晓，黄超：《基础教育中的学校阶层分割与学生教育期望》，《中国社会科学》，2016年第4期。，所以同时纳入平均家庭背景和学习成绩有可能存在共线性问题。如果不能像杨钋那样获得初期学习成绩*杨钋：《同伴特征与初中学生成绩的多水平分析》，《北京大学教育评论》，2009年第4期。，采用其他同伴指标分析影响学习成绩的同伴效应才是更好的选择。很遗憾，笔者并没有收集到具有初期学习成绩或其他生源质量指标的数据，所以在本研究中只好选择一些替代指标对同伴效应进行分析。另外，我们在分析同伴效应时，还应注意到其在不同群体中的作用可能具有差异*Ding, W., & Lehrer, S. F., “Do peers affect student achievement in china's secondary schools?”, in Review of Economics & Statistics, Vol.2 (2007), p.300-312.*Carman, K. G., & Zhang, L., “Classroom peer effects and academic achievement: evidence from a Chinese middle school”, in China Economic Review, Vol.2 (2012), p.223-237.*Lu, F., & Anderson, M. L., “Peer effects in microenvironments: the benefits of homogeneous classroom groups”, in Journal of Labor Economics, Vol.1 (2015), p. 91-122.。

需要注意的是，在分析同伴效应时也不应忘记教育资源投入的作用，因为在中国背景下，二者本身就具有很大的相关性，一个学校的教育投入状况可能会吸引不同的生源，从而组合成不同的同伴群体，不同的同伴组合又会产生不同的火花，影响到组合内部每位学生的学习成绩。由此，本文的分析框架和研究假设如下：

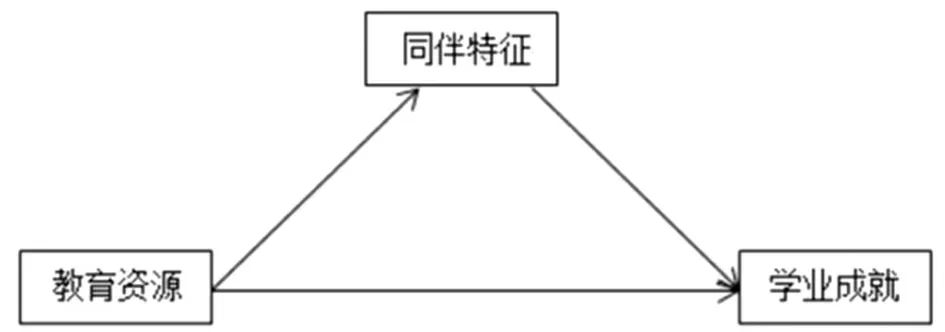
图1 分析框架

三、研究方法

(一)数据来源

本研究使用的数据是由经济合作与发展组织(Organization for Economic Co-operation and Development，OECD)发起开展的国际学生能力评估项目(Program for International Student Assessment，PISA)*关于PISA2015项目的介绍均来自OECD的PISA官方网站：http://www.oecd.org/pisa/ ，要了解更多此项目的信息，请参考网站内容。2015年中国四省市的调查数据。PISA自2000年开始，每三年举行一次，中国上海在2009年正式加入，而到2015年，中国首次以国家身份正式参加，选取了北京、上海、江苏、广东四省市作为调查点。PISA项目的研究对象是就读于各级各类教育机构7年级及以上的15岁在校生。经过学校和校内学生两个阶段的科学抽样，我国在以上四省市中共有268所学校的9841位学生有效完成了调查测试。但是，有些学生的部分变量存在缺失值，剔除了本研究中所有变量的缺失样本后，最终获得了256所学校的8658份样本。样本均值T检验结果表明，样本变量值的缺失是随机的，所以，样本的剔除并不影响分析的结果。

PISA项目所关注的不仅仅是学生是否掌握相应的学科内容，更主要的是评价学生在义务教育即将或刚刚结束时，学生是否具备参与未来社会所必需的知识和技能。2015年的测试内容包括数学、阅读、科学、财经四个方面的素养，其中对科学素养的测试是2015年的主要测试领域。所以在本研究中主要对影响15周岁学生科学素养成绩的学校因素展开分析。

(二)变量

本文的因变量是每位学生的科学素养成绩，在PISA2015中，对科学素养成绩的测试结果并不是一个具体的分数，而是以Rasch模型估计出的十个“拟真值”(Plausible Values， PV)。PV是在估计学生能力时，除了考虑学生答题反应外，再加入相关背景变量估计学生能力值的概率分布，从中随机抽取能力值，呈现学生该领域分数的可能范围。

本文的自变量包括两部分：第一部分是学生所在学校的资源配置情况，由学校可以向学生提供的活动数量、科学教研组设备水平、学校教师具有本科学历的比例三个变量按照主成分分析法整合成一个综合的教育资源投入变量*节省篇幅，模型中所用变量的具体处理过程不再详细展示，如果需要可联系作者获取。；第二部分是同伴特征变量，包括同一学校学生家庭社会经济地位和日常表现的均值与标准差。其中家庭社会经济地位是由父母最高职业地位、父母最高教育程度、家庭物品拥有量三个指标整合而成。日常表现是由学生迟到、逃课、逃学等失范行为发生的频率，进取心，科学课堂纪律，对科学的兴趣四个指标整合而成。这些指标本身多是由OECD公布的经过处理后的变量*各个变量的具体处理过程和涉及到的问卷题目在PISA2015技术报告中有详细的介绍，详情请参见http://www.oecd.org/pisa/data/2015-technical-report/.。本文在最终的处理过程中已经将各个变量的方向调整一致，最终的数值越大，相应的程度越高。

除了自变量之外，本研究中还加入了其他可能会影响学生科学素养的一些变量作为控制变量，这些变量主要包括性别、就学阶段、学校位置、家庭社会经济地位。另外也将学生个人的日常表现纳入模型中，包括迟到、逃课、逃学等失范行为发生的频率，进取心，对科学的兴趣三个指标。另外，在分析自变量影响的群体差异时还用到学生在班级的表现变量，该变量被处理成二分变量，如果学生个人的综合表现高于学校平均值，赋值为1，否则赋值为0。

本文使用的所有变量的描述性统计结果参见表1和表2，这些变量共两个层次，样本量为8658的变量均为个人层次的变量，样本量为256的变量均为学校层次的变量。其中科学素养的均值和标准误(标准差列显示)是根据stata中的pv模块加权计算得出的，无法显示最小值和最大值。

表1所有连续变量的描述性统计

(三)研究方法

由于PISA2015的数据是多层的，个体的学生嵌套于学校层次，并且我们的两个解释变量在学校层次有很大的差异性，为了更好地解释学校教育资源配置与同伴特征对学生科学素养的影响，我们采用多层线性模型(Hierarchical Linear Model, HLM)进行统计估计。另外，因为我们的因变量是“拟真值”，所以在分析的过程中，我们使用的是stata中的pv模块进行多层线性模型的系数估计。

表2所有类别变量的描述性统计

根据杨菊华的介绍*杨菊华：《多层模型在社会科学领域的应用》，《中国人口科学》，2006年第3期。，多层线性模型的基本原理在于，它可以将因变量中的变异分解成两部分：一部分归之于寓于同一群体的个体差异(即“群内变异”)；另一部分归之于不同群体之间的个体差异(即“群间变异”)。通过分解变异，可以区分群体效果和个体效果，揭示群体与个体变量之间的关系。本文使用的两层线性随机截距模型的具体形式如下：

第一层(个体层次)：

(1)

公式(1)中，Yij和Xkij分别表示第j所学校第i个学生的学习成绩得分和个体层次n个解释变量取值，εij为个体层次的随机误差项，β0j是随机变量，表示第j所学校在所有解释变量为0时学生教育期望的取值(即截距)。

第二层(学校层次)：

(2)

βkj=γk，(k=1,2,…,n)

(3)

公式(2)中，Waj表示第j所学校的m个学校层次变量的取值，μ0j为学校层次的随机误差项，表示第j所学校学生科学素养得分与所有学生科学素养得分均值的离差，γ0表示在所有学校层次解释变量为0时学生科学素养得分(即截距)。将公式(2)(3)带入公式(1)可得到本文使用的模型，其中随机误差项均假定服从正态分布且相互独立：

(4)

四、研究结果

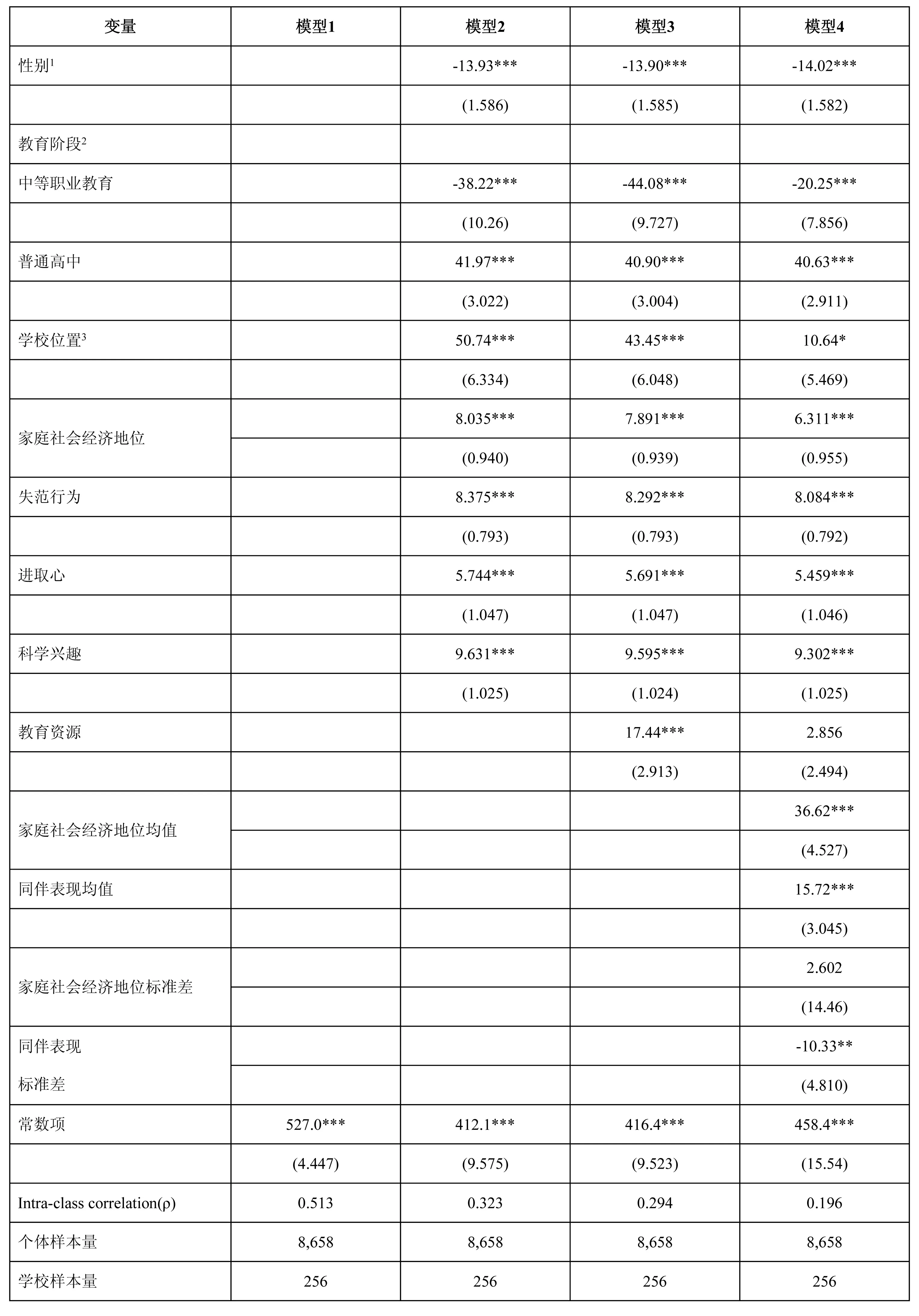
表3是我们是用两层线性回归模型对教育资源配置和同伴特征对学生科学素养得分影响进行的估计。在具体建模策略上，采用嵌套模型的方式，通过逐步在模型中加入变量的方式分析各类变量对学生科学素养defender净效应。模型1是没有纳入任何自变量的零模型，从模型的分析结果看，校间的关联度系数(ρ)为0.513，该数值表示校间的变异值占总变异值的比例，也就是说学生的科学素养有51.3%的可变性来自学校，48.7%的可变性来自学生。所以学校对学生科学素养的影响至关重要，这也表明多层次模型是比简单线性模型更加合理的估计方法。在模型2中，我们纳入了可能影响学生科学素养的性别、就学阶段、家庭社会经济地位、失范行为、进取心、科学兴趣等个人变量和学校位置作为控制变量，模型2是基准模型，这些因素是理论上可能会影响学生科学成绩但本文并不展开讨论的变量。

表3教育资源与同伴效应对学生科学素养的多层线性模型结果

注：括号中为标准误，*** p<0.01, ** p<0.05, * p<0.1。

1.男生为参照组；2.初中为参照组；3.县镇为参照组。

模型3在基准模型的基础上纳入了我们的第一个解释变量——学校教育资源配置情况。结果发现，学校教育资源配置对学生科学素养有显著的正向作用，资源配置每提高1个单位，学生的科学素养成绩将会提高17.44分，且该系数在1%的水平上显著。此时学生科学素养的校间关联度系数也从基准模型中的32.3%降低至29.4%，我们的假设1得到了验证。

模型4在模型3的基础上纳入了我们的第二个解释变量——同伴特征。结果发现，除了学校内部家庭社会经济地位的标准差变量不具有显著性，另外三个变量对学生的科学成绩均有显著影响，假设2.1、2.2和2.4均得到证实，假设2.3没有得到证实。家庭社会经济地位的平均值每增加1个单位，学生的科学素养就会提高36.62分。同伴日常表现的平均值每增加1个单位，学生的科学素养就会提高15.72分。而同伴表现差异性越大，学生的科学素养成绩就会越低。此时学生科学素养的校间关联度系数也从基准模型中的32.3%降低至19.6%，这说明学校的同伴特征对学生科学素养的影响是很大的，其影响程度甚至高于学校教育资源配置的影响程度。

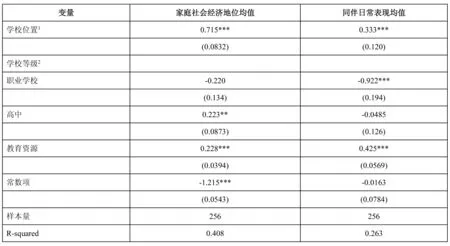
另外需要注意的一点是，在我们纳入同伴特征变量之后，原本显著的教育资源配置变量却变得不显著了，并且系数也从17.44下降至2.856。但这并不表明教育资源配置对学生科学素养成绩没有影响，而是说二者之间存在中介效应，并且同伴特征是二者之间关系的唯一中介。为了进一步验证二者之间的中介是否真实存在，我们在学校层次上计算了资源配置变量对同伴特征的影响系数，模型加入了学校位置和学校等级作为控制变量，具体结果见表4。结果显示，教育资源配置每提高一个单位，该校学生的平均家庭社会经济地位会提高0.228个单位，平均日常表现会提高0.425个单位，且两个系数均在1%的水平上显著。这也就意味着较高的学校教育资源配置确实可以吸引家庭社会经济地位较高的学生和日常表现较好的学生。我们的假设3.1和假设3.2均得到了证实。这一统计结果也为刚刚的猜测提供了依据，教育资源配置对学生科学素养存在间接效应，而同伴特征是其唯一的作用中介。

表4学校教育资源配置对同伴特征的影响回归模型

注：括号中为标准误，*** p<0.01, ** p<0.05, * p<0.1。

1.县镇为参照组；2.初中为参照组。

综合来看，教育资源和同伴效应对学生的科学素养成绩确实产生了不同的影响，但这种影响有可能对不同群体的作用也是不同的，为了验证假设4，我们对不同性别和不同教育阶段的学生分别进行了多层线性模型估计结果的计算，具体结果见表5。根据统计结果，同伴的家庭社会经济地位结构对不同性别的学生的科学素养得分影响差别不大，但是同伴日常表现对女生的影响要大于男生，不管是均值还是标准差均是如此。就教育阶段而言，尽管教育资源配置的影响系数不显著，但其大小有很大的差异，在初中阶段影响最小，甚至在方向上是负的，而到了高中阶段影响系数显著提高。在不同阶段，同伴特征的影响具有很大差异，总体而言，初中阶段，同伴家庭社会经济地位的标准差的影响非常显著，且系数很大，这是其他任何阶段都没有的影响。笔者认为这主要是因为初中阶段是义务教育，学生家庭社会经济地位差异较大，而到职业教育阶段或高中阶段，很多低社会经济地位家庭的孩子放弃接受教育或没能通过上一阶段教育的入学筛选，使得总体学生家庭社会经济地位差异性较低。职业教育阶段同伴的平均家庭社会经济地位对成绩影响最为显著。高中阶段，同伴表现的影响较其他阶段更为显著，不论是均值还是标准差。总体而言，普通教育阶段的学生更容易受同伴日常表现的影响，而职业教育阶段的学生更容易受同伴家庭社会经济地位的影响。假设4得到验证。

表5教育资源与同伴效应对学生科学素养的群体差异

注：括号中为标准误，*** p<0.01, ** p<0.05, * p<0.1。

1.男生为参照组；2.初中为参照组；3.县镇为参照组。

五、结论与讨论

通过对国际学生能力评估项目2015年中国四省市的调查数据(PISA2015)的实证分析，本文探讨了学校因素中的教育资源配置和同伴特征对15周岁学生科学素养成绩的影响。研究发现：第一，学校的教育资源投入对学生的科学素养有正向的作用，但是这种作用并不是直接的，而是通过吸引具有较高家庭社会经济地位和日常表现的生源来实现的。第二，在同伴效应中，全校学生的平均家庭社会经济地位和日常表现对学生的科学素养具有正向作用，而日常表现的异质程度会阻碍学生科学素养成绩的提高。第三，同伴效应在不同学生群体中的作用并不一致，与男生相比，女生的科学素养水平更容易受同伴日常表现的影响，初中生的科学素养更容易受同校学生家庭社会经济地位异质程度的影响。职业教育阶段的学生更容易受同校学生家庭社会经济地位平均水平的影响，而普通教育阶段的学生更容易受同学学生日常表现的影响。

以上研究发现对我国中学的教育和招生政策、家庭的学校选择均有一定的参考价值。首先，加大对教育的投入尤其是高中阶段的教育投入仍然是十分必要的，因为教育资源配置对学生学习成绩的影响并不像有些学者分析的那样，它依然发挥重要作用。其次，对于初中教育，应尽量缩小同一学校内部学生家庭背景的差距，而到了高中阶段，同校学生家庭背景的差距所带来的负面影响已经不再显著，但是学生的日常表现在普通高中阶段开始发挥重要影响，所以建议普通高中的管理者一定要注意维护学校学生的日常表现，加强纪律管理，多鼓舞士气，提高全校学生的日常表现，缩小内部差异将在提高学生科学素养方面发挥积极作用。

当然，本文仍有不足之处，首先，由于缺乏初期的成绩对比，无法更好地控制学校内部生源的初始差异，难免存在一定的内生性问题。正如杜育红和袁玉芝在对国内教育中同伴效应研究的总结中指出的*杜育红，袁玉芝：《教育中的同伴效应研究述评:概念、模型与方法》，《教育经济评论》，2016年第3期。，我们应该采用随机试验、自然实验以及准实验的因果推断研究更好的分析同伴效应在学生学习成绩中的作用，显然本文还没有很好地解决这一问题。但是本文也做了尝试，利用多层线性模型加控制变量的方式尽可能地控制生源的选择机制对结果造成的干扰。