立体几何初步学习漫谈
徐永忠
认识空间图形,培养和发展空间想象能力、推理论证能力、运用图形语言进行交流的能力以及几何直观能力,是高中阶段数学必修课程的基本要求.下面主要谈谈学好这部分内容需要注意的几个方面,希望能够对大家有所帮助,
一、学好概念打基础
有些同学平时不重视基本概念的学习,或多或少存在类似的想法:定义是否掌握没有关系,只要会做题就行.岂不知这种所谓的“会”做题是不牢靠的,经不住考验的.随着学习内容的增多,知识点的交汇,概念就会模糊不清,似是而非,导致推理论证不严谨,甚至出错。
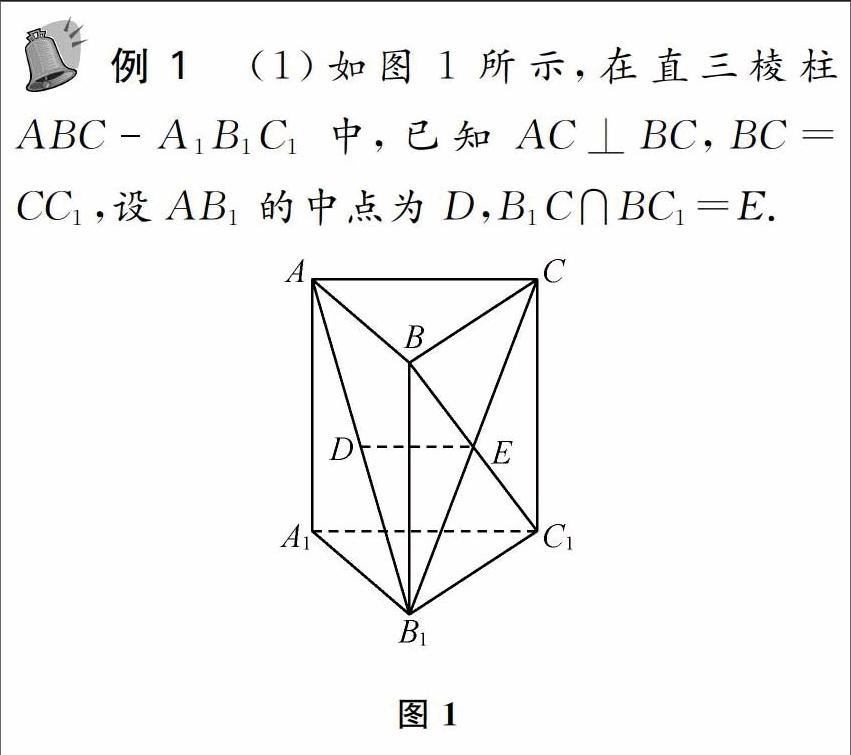
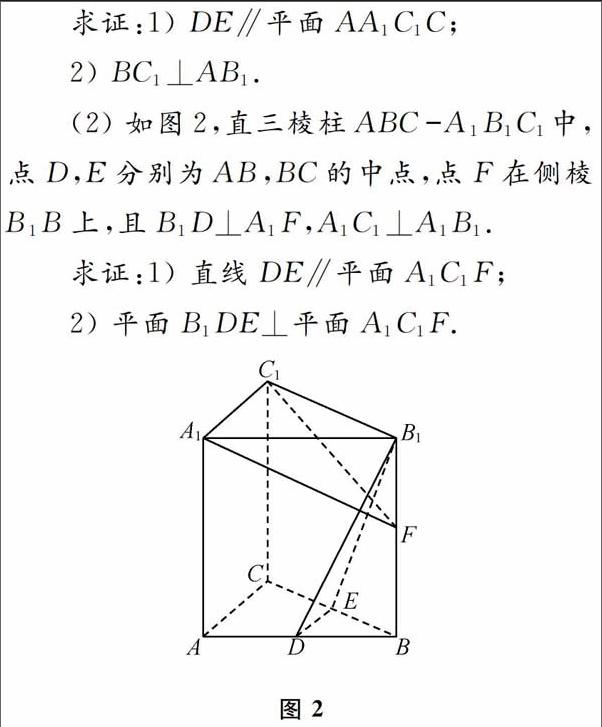
我们在高考阅卷中也发现过这种情况,根据阅卷的规范化要求,就不能得分.如下面两题都以直棱柱为载体,进行推理论证。
在第(2)问的证明中,都要用到直棱柱的概念,即侧棱与棱柱的底面垂直的棱柱.如果在答卷中跳过了这个概念,直接用到线线垂直,则说明概念不清、推理不严谨,从而不能得分。
义如异面直线所成角的概念,有些同学在练习中常会因为对角的范围考虑不清楚致错.我们通过概念的形成过程来理解,就能够掌握概念,防止出错.两条异面直线,肯定不平行、不重合,因而所成角不会为0°,义异面直线所成角的定义方式是通过平移变成相交直线,而相交直线的夹角的范围不会超过90°。这也是“转化”思想的应用.
再如二面角的平面角概念,学习的时候要抓住要点:
①顶点必须在两平面的交线上;
②两边分别在两个半平面内;
③两边必须垂直于该交线,
再配合不同位置的圖形,大家对这个概念的理解就能比较准确,
二、掌握定理学方法
公理、定理是进一步学好立体几何的重要内容,是进行逻辑推理的重要依据.因而大家要重视对公理、定理的理解和应用。
1.对公理、定理本身的学习理解
四条公理是立体几何推理论证的基础,要在理解的基础上加以记忆、应用。
定理本身的证明具有示范性、典型性,它体现了基本逻辑推理知识和基本的证明思想的培养,以及规范的书写格式的养成,要进行严格训练。
如课本内有一条定理,“过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线”,利用具体实例初步使用了反证法手段进行了推理,为后续“直线与平面垂直的性质定理”的证明使用反证法做了铺垫。
由此可见,反证法是一种比较重要的数学证明方法.所以我们对反证法的证题思想、一般步骤、书写格式、注意要点等都要掌握到位,这对大家证明立体几何问题及其他数学问题,会很有帮助。
2.熟练运用定理分析问题、解决问题
在空间直线、平面的平行和垂直关系的判断与证明问题中,首先要理解、掌握、记忆相关定理,定理与定理之间,定理与其他知识之间的联系,使知识系统化;同时定理的学习是为了应用,所以有针对性地进行定理应用的练习,在应用中加深对定理的理解运用(如条件、结论、证明、适用场合等)。
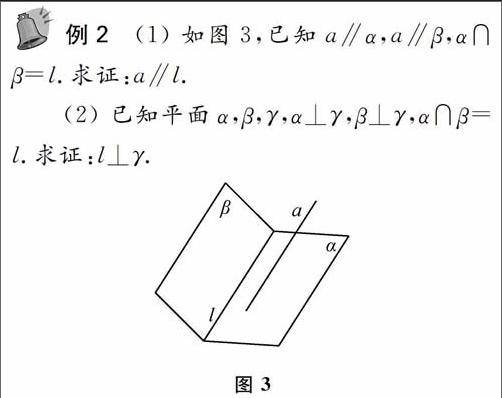
在这两个命题的证明中涉及线面平行、线面垂直的诸多定理,还要添加适当的辅助线,这对于训练同学们对定理的运用能力是很有益的,同时这两个命题对于理解线面关系也是大有好处.像这些重要结论可以帮助大家很快地解决选择题或者填空题,对于一些解答题虽然不能直接应用,但是它能够帮助我们打开解题思路,进而求出答案。
三、用好类比涨能力
学好立体几何其中一个重要方法就是类比.类比是根据两个对象在某些方面的相同或相似,推出它们在其他方面的相同或相似的一种推理方法,由于类比推理所得结论的真实性并不可靠,因此不能作为严格的数学推理方法,但是它是提出新问题和获得新发现的不竭源泉。
平面几何是我们所熟悉的,而立体几何与其在很多方面是相同或相似的,因此在两者之间进行类比是研究它们性质的一种非常有效的方法。
四、体会“转化”育素养

