从空间到平面
端木彦


解决立体几何问题的一个基本原则就是空间问题平面化,这里面蕴含着降维转化思想.将三维的空间问题转化为二维平面问题,不仅可以降低思维的难度和运算的复杂程度,还能帮助我们消灭多余信息所造成的思维误差,大大提高思维的精准度。
一、图形维度的转化
课本上,将棱柱描述为平面多边形沿某一方向平移形成的空间几何体,将圆柱、网锥、圆台描述为平面多边形绕它的一边旋转一周形成的几何体.再经历投影、三视图、斜二测画法等内容的学习,帮助我们从不同的角度感受几何体的平面特征.
这些知识的学习,既培养了我们的识图能力与空间想象能力,又为后面空间关系的转化打下了基础.
面动成体,空间问题从平面中来,最终再回到平面中去,
二、位置关系的降维转化
证明线面平行与垂直、面面平行与垂直,通常运用降维转化的思想方法,通过平面几何的一些已知结论证明三维立体的一些结论.这种思想方法渗透在立体几何各个定理和结论的推导和形成过程中.
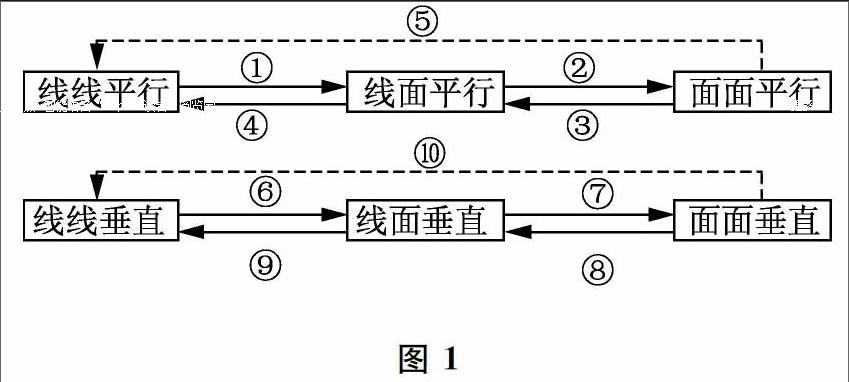
我们常用类似下面的图表来体现空间位置关系相关定理与结论之间的关系:
其中③指的是“如果兩个平面平行,那么其中一个平面内的任意一条直线与另一个平面平行”;⑨指线面垂直定义的逆用,即“一条直线与一个平面垂直,则该直线与平面内的任意一条直线都垂直”;其他的数字路径课本中都给出了对应定理。
图表中的各条数字路径均体现了降维转化思想在立体几何证明中的运用。
如路径④,如何在平面内找到与面外直线平行的直线,是一个典型的空间问题.联系直线与直线的位置关系,最终引入经过已知直线的另一个平面,两平面的交线即为所求.这样,将空间问题平面化,思维难度得以降低。
义如路径⑤,在两个平行平面中如何寻找两条相互平行的直线呢?通过引入第三个平面使空间关系平面化,将问题解决。
再如路径⑩,其实就是利用了二面角的平面角,再次将空间问题平面化。这种降维平面化的思想在解决复杂问题时对理清思路很有帮助.
三、数量关系的降维转化
1.空间角转化为平面角
经过空间任意一点O,分别作两条异面直线的平行线,这两条平行线所成的锐角(或直角)即为异面直线所成角。这一过程,将空间两条异面直线转化到同一平面内去研究大小,实际上也是将三维空间中的两条直线降维转化为二维平面图形,再利用平面几何知识去解决问题。
2.空间距离转化为平面距离
四、总结
立体几何中蕴含着丰富的数学思想,其中最重要的就是降维转化思想,它通过降低问题所属背景的维度,化生为熟,化繁为简。它贯穿立体几何学习的始终,是解决立体几何问题所共通的方法。
熟练运用降维转化思想,不仅对立体几何问题的求解有重要意义,更可以迁移到其他章节知识的学习中,有机整合,合理运用,形成解决相关问题的有效策略。

