漏磁检测中油管螺旋传送装置运动学和动力学分析*

龙再勇， 唐东林， 王 斌， 张文文， 赵 江

(1.西南石油大学 机电工程学院，四川 成都 610500； 2.新疆克拉玛依市金牛工程建设有限责任公司，新疆 克拉玛依 834008)

0 引 言

油管是石油钻井过程中必不可少的常用材料，常年工作在具有腐蚀性介质的井下。在鼓胀效应、温度效应和螺旋弯曲等的作用下，油管承受复杂载荷，产生弯曲变形或螺旋变形，因而经常造成油管失效[1]。油管的失效形式可以概括为横向缺陷失效和纵向缺陷失效两种。横向缺陷指与油管轴线方向垂直的缺陷损伤，主要包括横向裂纹、孔洞、管壁腐蚀等；纵向缺陷指与油管轴线方向平行的缺陷损伤，主要包括纵向裂纹、纵向破裂、偏磨等[2]。缺陷大多发生在油管的局部，绝大部分油管通过一定的检修还可以继续使用。为了降低采油成本，提高开发效益，国内外各油田都十分重视研究油管缺陷检测技术。

装置采用的检测方法是由对辊轮驱动油管作螺旋推进运动通过缺陷检测探头完成检测。在检测过程中油管螺旋运动所形成的螺距与检测探头长度的匹配直接关系到能否对油管进行全覆盖检测，油管螺旋运动过程的平稳性也影响着检测信号的信噪比和检测的灵敏度[3]。所以有必要对该装置的运动进行研究分析，由于该装置影响其功能的主要运动是对辊轮驱动油管的螺旋前进运动，所以在此，仅对该螺旋推进运动做较深刻的分析。

装置的动力学分析对研究整个装置的运动有很大的影响，通过对装置的动力学分析，可以得到整个装置的运动情况，油管运动速度的平稳性，加速度的大小，是否会产生滑动摩擦等。所以对整个传送装置进行动力学分析十分必要，包括油管从速度为零加速到匀速前进状态的加速过程分析和匀速阶段油管、对辊轮、压轮三者的动力学分析。

1 油管螺旋传送装置的运动学分析

为了实现螺旋推进运动，且满足检测过程可靠性高、精度高、检测速度高的要求，根据设计要求，该装置的检测速度定为30 m/min，检测探头的长度不大于250 mm，油管检测的重合度大于等于120%。根据公式可计算螺距的最大值。

P=L/M

(1)

式中：P为油管螺距；L为检测探头长度；M为检测重合度。

计算得螺距的最大值P为208 mm。

1.1 对辊轮驱动结构数学建模分析

假设对辊轮与油管为刚性作用，相互接触的地方不产生形变，则对辊轮驱动油管时都是以点接触相互作用。设对辊轮主动轮与油管的接触点为C，以C点为坐标原点，以通过C点且垂直于油管轴线的横截面为XY平面，油管轴向为Z轴方向建立笛卡儿直角坐标系[4]。具体模型如图2所示。

图1 油管螺旋传送对 图2 螺旋推进运动数 辊轮驱动原理 学模型

其中：平面α为对辊轮所在平面；平面β为油管切点所在的切平面；V为对辊轮转动的线速度；θ为面α与油管轴线方向YZ面间的夹角；φ为辊轮与油管接触点所在法线与水平面的夹角。

假设对辊轮与油管之间为纯滚动，无滑动摩擦，根据其空间关系，可以建立如下方程：

Vx=Vxz·sinθ=V·sinφ·sinθ

(2)

Vy=V·cosφ

(3)

Vz=Vxz·cosθ=V·sinφ·cosθ

(4)

(5)

(6)

式中：D为油管外直径；P为油管螺旋的螺距。

D已知为73 mm，θ经过不断的优化设计，确定为60°，中间角度参数φ可以通过计算得出，因此可以最终算出螺距P。

计算φ角的方法有很多种，可以用三维建模设计软件Pro/E、solidworks等求解，也可以用动力学仿真软件ADMAS等求解。最简单的方法是建立数学模型求解，将笛卡儿直角坐标系中空间关系向XY面(也可以向α面)投影,获得φ的投影角，然后通过建立平面方程求解获得φ的投影角以及φ角。最终求解得φ角为44°。

将已知数据代入上述方程中可算出螺距P=91 mm。计算出的最大螺距为208 mm，螺距P小于最大螺距，所以符合不发生漏检的要求。

1.2 压轮摆放角度的确定及运动学分析

通过对对辊轮结构的数学建模分析，得到了油管螺旋的螺距P、周期T和检测速度Vz，油管螺旋运动时在其油管的一侧固定位置做一个标记，可以得到油管的螺旋线，截取一个周期的螺旋线做如下分析。

将一个螺旋周期的油管沿轴线方向截开，可得如图3所示的油管螺旋线展开图，其中A表示螺距P，B表示油管外直径，C为螺旋线与油管横截面的夹角，即油管最高点的瞬时线速度与油管横截面的夹角。

φ，A和B已知，可以通过公式tanC=A/B计算得C为21.7°。

图3 油管螺旋线示意图

压轮安装在油管的正上方，其接触点在油管的最高点。为减少压轮对油管螺旋运动的阻碍，尽可能的使压轮的旋转线速度方向与油管最高点的速度方向相同，使油管与压轮之间纯滚动，不产生滑动摩擦力。为了达到这种效果，压轮安装时的安装角度应与油管最高点速度方向的角度一致。压轮的转动是通过油管与压轮之间静摩擦力产生的，油管和压轮之间没有相对滑动，压轮的线速度与油管最高点的速度相同。

2 油管螺旋传送装置的动力学分析

2.1 加速螺旋前进阶段的动力学分析

假设对辊轮与油管为刚性作用，相互接触的地方不会产生形变，对辊轮驱动油管时都是以点接触相互作用。

首先，当油管刚与对辊轮接触时，对辊轮中的主动轮在电机的驱动下一直在转动，在主动轮和油管之间产生一个相对运动，因而产生滑动摩擦，在滑动摩擦力的作用下，油管开始螺旋运动。油管运动在油管和从动轮之间产生相对运动，因而从动轮又在滑动摩擦力的作用下开始转动。随着油管和从动轮在滑动摩擦力的作用下不断加速，当加速到三者相互接触点的线速度相同时，之间的相对运动消失，它们之间的滑动摩擦也就迅速变为静摩擦，之后油管将在静摩擦力的作用下匀速螺旋前进。

分析该阶段滑动摩擦力的变化，由式Ff=μ·N得，该阶段油管与主动轮之间的正压力N没有变化，摩擦因素μ也不变，所以滑动摩擦力Ff也不变。同理可得油管与从动轮之间的滑动摩擦力的大小也不改变。

2.2 匀速螺旋前进阶段的动力学分析

匀速螺旋前进阶段的动力学分析主要是对在匀速阶段油管、对辊轮、压轮三者之间的接触点的分析。该阶段，油管在主动轮的驱动下螺旋前进，从动轮和压轮在油管的驱动下做旋转运动，相互之间的驱动力都是静摩擦力。

从以下四种受力模型对该阶段油管进行受力分析，这些分析都是建立在油管、对辊轮、压轮都是刚性作用，不产生形变的基础上。

模型一：对模型绘制空间受力分析示意图难度较大且各力的相互间的关系不好表达，所以从该模型的两个方向的投影进行受力分析：①从上向下投影的模型进行受力分析，如图4所示；②与对辊轮平面平行的平面投影的受力分析，如图5所示。

图4 模型一油管受力 图5 模型一油管受力 分析图1 分析图2

其中：Ff1为对辊轮主动轮对油管的静摩擦力；FN1为对辊轮主动轮对油管的支撑力；Ff2为对辊轮从动轮对油管的静摩擦力；FN2为对辊轮从动轮对油管的支撑力；Ff3为压轮对油管的静摩擦力；FN3为压轮对油管的压力；G为油管重力的集中力。

由受力分析可得，该模型为一个空间平衡力系，由空间平衡力系的平衡方程可以得出各力间的相互关系。

(7)

(8)

为了便于分析，在该模型与对辊轮平面平行的平面建立笛卡尔直角坐标系,如图6所示。

其中：原点O在对辊轮主动轮的质心；XY平面与对辊轮平面平行；Z轴垂直与XY平面与油管轴线成30°夹角。

根据空间平衡力系公式可以得出该模型具体的空间平衡力系方程：

(9)

(10)

式中：β为对辊轮与油管接触点所在法线与水平面XZ的夹角；θ为对辊轮平面与压轮平面的夹角；L为压轮与油管接触点到平面XZ的距离；r为对辊轮半径。

由方程解得：

Ff1=Ff2

(11)

FN1=FN2

(12)

2FN1sinβ=FN3+G

(13)

模型二：同样从该模型的两个方向的投影进行受力分析，分别如图7、8所示。

模型二的空间平衡力系方程为：

(14)

(15)

方程解得：Ff2sinβ=-FN2cosβ，Ff2和FN2都是正值，sinβ和cosβ也为正值，所以该等式不成立。模型二的空间平衡力系方程解出的等式不成立，所以该力学模型也不成立。

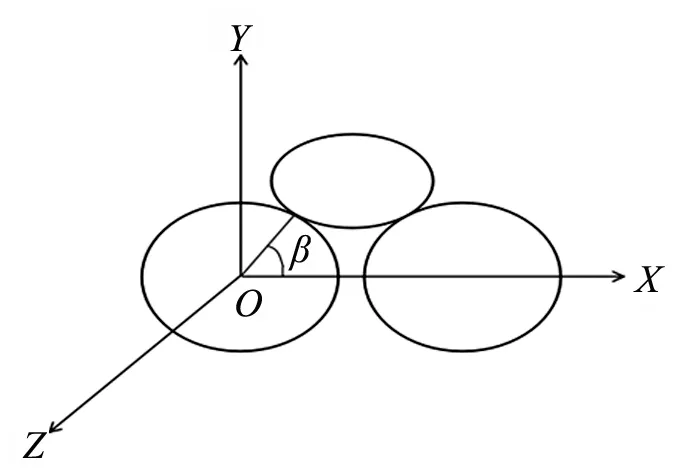
图6 对辊轮横截面投影图

模型三：具体力学模型如图9、10所示。

图7 模型二油管受力分析图1 图8 模型二油管受力 分析图2

模型三的空间平衡力系方程：

(16)

(17)

式中：α对辊轮横截面与油管横截面的夹角；γ力FN1与水平面XZ的夹角。

由方程解得:rsinβ=L，但根据实际得，rsinβ与L显然不相等，所以该等式不成立。模型三的空间平衡力系方程解出的等式不成立，所以该力学模型也不成立。

模型四：具体力学模型如图11、12所示。

图9 模型三油管受力 图10 模型三油管受力 分析图1 分析图2

模型四的空间平衡力系方程：

(18)

(19)

由于该方程较复杂，直接进行代数化简难度比较大，所以将具体数值代入方程。解得-1000Ff1-8FN1-500Ff2-542(FN3+G)=0,由于Ff1、FN1、Ff2、FN3和G都是正值，所以可得该等式不成立。模型四的空间平衡力系方程解出的等式不成立，所以该力学模型也不成立。

对油管匀速螺旋阶段的受力情况建立四种受力模型进行分析，分析发现，只有模型一的空间平衡力系方程解出的等式成立，所以这四种受力模型只有模型一能够满足要求。

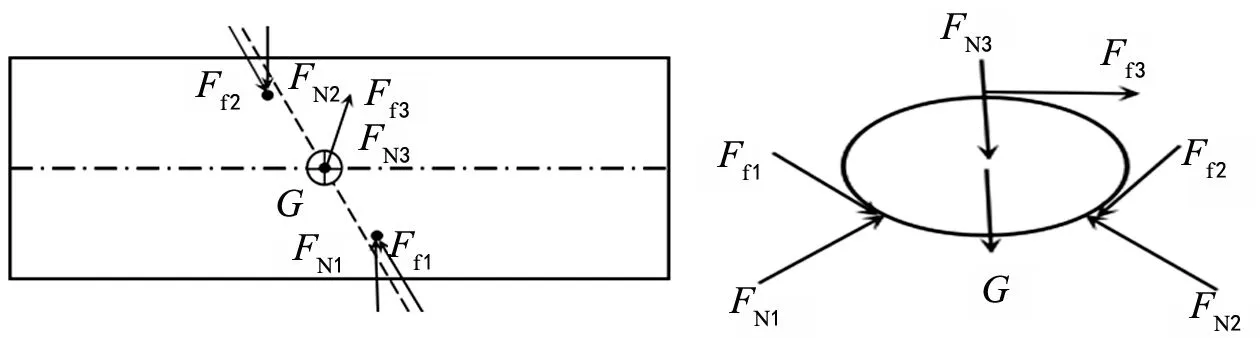
图11 模型四油管受力 图12 模型四油管受力 分析图1 分析图2

3 基于ADAMS软件油管螺旋传送装置的仿真分析

利用三维建模软件建立螺旋传送装置的三维模型，然后将其导入ADAMS软件进行运动学和动力学仿真分析。运动学仿真包括油管质心位置、质心速度、质心加速度等；动力学仿真则主要是油管在XYZ三轴方向上的具体受力情况。

3.1 油管螺旋传送装置的运动学仿真分析

(1) 油管运动质心位置变化的分析

如图13所示，油管质心位置运动曲线的走势为，在开始短暂阶段呈水平状态，之后呈一条斜率固定的倾斜直线。分析可得，油管质心位置曲线开始阶段的水平状态表示油管还未开始螺旋运动，之后斜率固定的倾斜直线表示油管沿Z轴的运动速度恒定，油管质心位置均匀变化。仿真分析结果与理论分析的结果完全一致。

(2) 油管运动质心速度变化的分析

如图14所示油管质心速度的曲线可分为水平阶段、倾斜阶段和水平阶段三个阶段。

结合理论分析可得，开始的水平阶段表示油管的运动速度为零，油管还未与辊轮接触；倾斜阶段则表示油管在对辊轮的带动下，开始做加速运动，理论分析该阶段的斜率应该不变，加速度恒定。加速的后半段出现了斜率变小的情况，经过分析得，出现这种状况的原因可能是油管和对辊轮是刚性接触，它们之间产生了碰撞，导致油管的部分被弹起离开对辊轮，致使驱动整个油管运动的摩擦力减小，因而导致加速度出现波动。第三阶段的水平状态则表示油管经过加速阶段后，当油管与主动轮接触点的速度达到一致时，他们之间的滑动摩擦变为静摩擦，油管做匀速螺旋前进运动。但从图中可以发现，该阶段总体呈水平状态，但在局部位置还是出现了波动。分析得该波动出现的原因是由于油管与对辊轮之间产生了碰撞，在油管的局部位置出现油管与对辊轮脱离的状况，导致速度出现波动。尽管油管的前进速度出现了波动，但由图可得其速度都是在-500 mm/s上下波动，而理论计算的油管检测速度为0.5 m/s，所以该模型的前进速度是符合检测速度要求的。

图13 油管质心位置 图14 油管质心速度 示意图 示意图

(3) 油管运动质心加速度变化的分析

如图15所示，油管的质心加速度曲线走势可分为水平阶段和水平波动阶段两个阶段。分析可得水平阶段是因为油管未与对辊轮接触，加速度为零；波动阶段应分为两个阶段，即油管最初的加速阶段和加速完成后的波动阶段。由于加速阶段很短，不进行具体分析。油管在加速完成后本应该保持匀速运动，加速度为零的状态，然而却产生图中所示的波动，分析得原因和速度波动原因一致，由油管和对辊轮之间的碰撞造成的。

(4) 油管运动质心角速度变化的分析

如图16所示，油管运动质心角速度变化仿真曲线。结合理论分析得，角速度开始阶段为零的水平线表示油管未与对辊轮接触；后面斜率基本不变的斜线表示油管在对辊轮的驱动下，做匀加速螺旋运动；最后阶段的波动直线则表示油管将维持加速结束后的角速度不变，角速度波动的原因是由于油管与对辊轮之间的碰撞。经理论计算油管角速度为2 103 °/s，仿真结果为角速度在2 050 °/s附近波动，两者之间的差距不大，所以该仿真结果符合要求。

图15 油管质心加速度 图16 油管质心角速度 示意图 示意图

(5) 油管运动质心角加速度变化的分析

如图17所示，油管运动质心角加速度变化仿真曲线。由图分析可得，油管质心的角加速度曲线走势可分为最开始的水平阶段和后面的水平波动阶段两个阶段。由于角加速度与加速度曲线走势相同，且分析的结果也相同，所以在此就不再进行赘述。

3.2 油管螺旋传送装置的动力学仿真分析

(1) 油管螺旋运动X轴方向的受力分析

如图18和图19所示，某组对辊轮作用下的油管X轴方向的受力情况。从图中可以看出，主动轮对油管施加的力为正，从动轮施加的力为负，且两力的波动都非常大，最小可为零，最大可达上万。理论分析时，两轮的力都是一个定值且相等。分析模型的仿真过程发现，由于设置的接触力为弹性碰撞，在仿真过程中，尽管有压轮作用在油管上，油管还是会产生跳动，导致作用在油管上的力发生变化，且作用力的值远远大于理论分析时的定值力。尽管作用力的值波动很大，但发现主从动轮的波动值的大小都在7 500 N附近，说明主从动轮对油管作用力的情况应该是基本相同的，这与理论分析的结果也相符合。

图17 油管质心角加速度 图18 主动轮施加在油管 示意图 上的作用力在X轴 方向的投影

如图20压轮对油管作用力在X轴方向的投影所示，结果与理论分析完全不同，由于压轮与油管的弹性碰撞，导致压轮对油管作用力在X轴方向的投影波动非常大。当压轮被弹起，与油管未接触时，作用力就为零，而当压轮向下运动与油管接触时，作用力就变得很大。

图19 从动轮施加在油管上 图20 压轮施加在油管 的作用力在X轴方 上的作用力在X 向的投影 轴方向的投影

(2) 油管螺旋运动Y轴方向的受力分析

如图21、22主从动轮对油管作用力在Y轴方向的投影所示。

图21 主动轮施加在油管上 图22 从动轮施加在油 的作用力在Y轴方 管上的作用力在 向的投影 Y轴方向的投影

从图中可以看出主从动轮对油管的作用力都是正值，与X轴方向作用力的投影一样，由于对辊轮与油管的弹性碰撞，导致作用力的波动非常大。当油管被弹起离开对辊轮时，作用力为零，当油管与对辊轮接触时作用力变得很大。但主从动轮力的波动情况相似，都在7 000 N附近波动，也说明主从动轮对油管作用力情况相同，符合理论分析的结果。

如图23压轮对油管作用力在Y轴方向的投影所示。从图中可以看出，该作用力的值为负值，符合理论分析的结果，但与X轴方向的投影一样，该作用力的波动也很大，分析其原因可得与X方向波动的原因一样，都是由油管与压轮之间的碰撞造成的。

(3) 油管螺旋运动Z轴方向的受力分析

如图24和图25所示。从图中可以看出，主动轮对油管作用力在Z轴方向的投影为负值，从动轮为正值。理论分析时的结论为Z轴方向的作用力为定值，仿真结果发现，Z轴方向的作用力与作用力在X、Y方向的投影一样，作用力的波动非常大，但主从动轮的受力情况却基本相同，符合理论分析的结果。其原因也与前述一样，所以在此不再进行赘述。

图23 压轮施加在油管上 图24 主动轮施加在油管 的作用力在Y轴方 上的作用力在Z 向的投影 轴方向的投影

如图26压轮对油管作用力在Z轴方向的投影所示。理论分析时得压轮对油管作用力在Z轴方向的投影为零，但从图中可看出压轮对油管作用力在Z轴方向的投影与理论分析完全不一样，由于压轮与油管的弹性碰撞，导致压轮对油管作用力在X轴方向的投影波动非常大。其原因与X轴方向分析的原因一致，在此就不再进行阐述。

图25 从动轮施加在油管 图26 压轮施加在油管 上的作用力在Z 上的作用力在Z 轴方向的投影 轴方向的投影

4 结 语

在油管的漏磁检测系统中，油管的运动状态对漏磁检测的影响非常巨大，所以有必要对油管螺旋运动过程中的运动学和动力学进行分析，从而提高油管检测的精度和灵敏度。

对油管螺旋运动的过程进行理论的运动学和动力学分析，利用ADAMS软件对油管的运动过程进行仿真分析。对比理论分析和仿真分析的结果发现，实际油管运动过程非常的不平稳，波动巨大，通过分析得产生波动的原因是由于油管在运动过程中与对辊轮产生刚性碰撞，导致油管在螺旋运动过程中不断的波动，影响检测结果。

后续工作将从利用ADAMS软件入手，对发现问题的模型不断的进行优化，使装置模型达到缺陷检测的要求，再根据软件模型进行试验验证。

[1] 许秀英.油管缺陷的无损检测[D].大庆：大庆石油学院,2005.

[2] 邹应国.油管纵向及横向缺陷自动检测系统的研究[D].武汉：华中科技大学,2005.

[3] 孙燕华,康宜华,刘涵君.基于ADAMS的钢管漏磁检测螺旋推进运动的计算分析[J].钢管,2011,40(1):60-64.

[4] 孙燕华,康宜华,谭 波.高速漏磁探伤中钢管螺旋推进参数设计与分析[J].机械与电子,2007(11):7-9.