高中数学新课程下学生自主学习能力的培养

福建省莆田第十一中学 林永生

高中的数学教学，要求老师在教学的过程中，开展多样化的教学方式；同时，也要求学生富有自主学习的能力。尤其是《普通高中课程标准实验教科书》数学必修系列，教材中新增了学生的实习作业，这一部分的内容更需要学生具有良好的自主学习的能力。我校结合新课程的教学需要，开展任务型的教学，同时，培养学生自主学习的能力，取得了立竿见影的效果。作为教学一线的老师，我在开展任务型教学的同时，着力做好学生自主学习能力的培养，具体体现在以下几个方面：

一、在课前，引导学生完成“知识预览”试卷——这是培养学生自主学习能力的前提条件。根据任务型的教学方法，在每一个知识块教学之前，老师根据这一节的内容，提前出一份“知识预览”试卷，把这一节的定义、主要内容、典型例题、注意问题一一列举出来，让学生在课前做好预习工作，带着问题上课。例如：在解析几何直线与圆的关系这节课之前，在“知识预览”试卷中，提出的问题节选如下：

1.如何判断直线与圆的位置关系？

2.已知圆外一点，求圆的切线，有几条？如何求解？

3.已知圆上一点，求圆的切线，有几条？如何求解？

4.已知切线的斜率，求圆的切线，有几条？如何求解？

5.在直线和圆相交时，如何求相交的弦长？等等。

二、在课堂上，实行小组合作的学习方法——这是培养学生自主学习能力的核心部分。在老师的引导下，各小组带着“知识预览”试卷中的问题，互相质疑、互相解答，共同完成课堂教学工作，同时，老师把本节课的重点、难点、关键的知识点、典型的题型一一解答。

例如：在抛物线定义这节课的教学过程中，分析完抛物线的定义，紧接着，请A小组的a同学回忆椭圆和双曲线标准方程的推导方法，运用解析几何常用的方法——直接法，引导他在黑板上求出开口方向向右的抛物线标准方程：y2=2px(p＞0)，并正确画出图形，焦点与准线。

同时请班级中其他的B，C，D三组派代表推导不同开口方向时的抛物线的相应的方程，五分钟后，B小组的b同学也运用直接法在黑板上推导出开口方向向左的抛物线的标准方程为：y2=-2px(p＞0)并正确画出图形，焦点与准线。

C小组的c同学很快就写出开口方向向上的抛物线的标准方程为：x2=2py(p＞0)并正确画出图形，焦点与准线。我当时觉得很奇怪，以为他是参考课本中的结论写出的。就问他得出标准方程的理由，他却很简单地描述：我只需把x轴和y轴交换一下，就把开口方向向上的抛物线转化为开口方向向右的抛物线，从而，根据开口方向向右的抛物线的标准方程：y2=2px(p＞0)写出。教室里顿时响起了热烈的掌声。

D小组的d同学也很快就写出开口方向向下的抛物线的标准方程为：x2=2py。并阐述说是根据开口方向向右的抛物线标准方程的推导过程写出的，这下，教室里像炸开了窝的蚂蚁一样，有说对的，也有说错的。这时持反对意见的一同学站起来说：“开口方向向下的抛物线的标准方程为：x2=-2py(p＞0)。”d 同学也不甘示弱地争辩着：“我所写的方程为：x2=2py(p＜0)，还不是一样吗？”教室里的气氛更热烈了。我只好请同学们注意p的几何意义，这时，数学课代表站起来说：“p的几何意义表示焦点到准线的距离，只能是p＞0，所以，开口方向向下的抛物线的标准方程为：x2=-2py(p＞0)。”我见时机已成熟，就适时在黑板上写出抛物线的四种不同形式下的标准方程，并对p的取值范围和几何意义作进一步的强调。

最后，我进一步提出问题：“面对着抛物线的四种不同形式下的标准方程，该如何去理解并记住呢？”教室里再次沉默下来了。两分钟后，善于观察的C小组的同学又很快就站起来说：“可以根据不同形式的抛物线上的点的横、纵坐标的符号结合标准方程的形式去理解和记忆。”我进一步让她作详细的解释……同学们紧皱的眉头终于展开了。

三、在课后，组织学生参加数学的研究性学习小课题——这是培养学生自主学习能力的升华部分。研究性学习小课题的材料是由学生自己搜集、整理、归纳。例如：学完必修2第二章点、线、面的位置关系之后，我布置同学们完成学习小课题——空间中的三类角的比较。

首先：材料的搜集：把本班的学生分成A、B、C三组，分别负责搜集空间中异面直线所成角、直线和平面所成角、平面与平面所成角（二面角的平面角）三部分的相关知识点，并强调注意不同类型的角的范围的区别，典型的例题的搜集，角的求法的总结（并配有相应的例题）等。

其次：数学研究性学习课题材料的交流与整合。

三个小组的学生进行材料交流、补充，归纳本小组的研究成果，整合在一起，共同完成这次有关空间的角部分的小课题，并在班级的学习角展示。这样，圆满地完成了这次小课题的作业与结题任务。

小课题作业：列表如下：

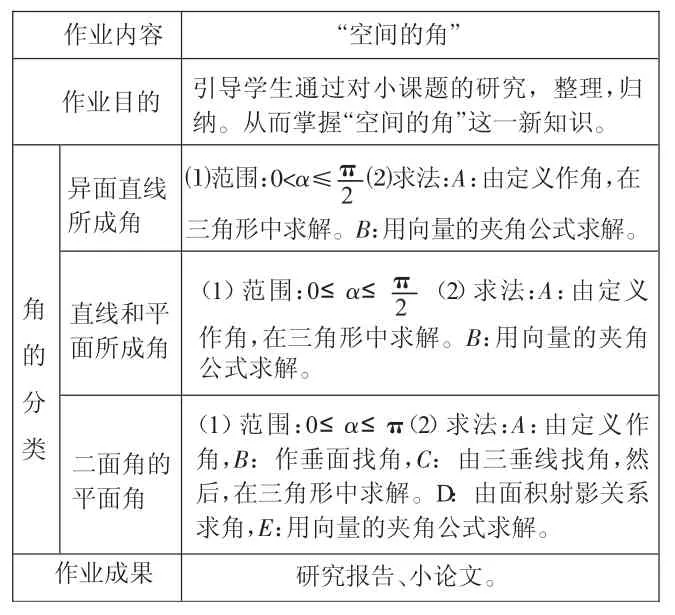
“空间的角”小课题作业表

在小课题的结题报告中，一并展示相应解法的例题，进一步巩固这一部分的内容。

最后：我通过多媒体对结题报告进行分析讲解，形象、生动地展示三种不同类型的空间的角，同时，比较三种角的范围、解法，尤其是向量法在三种角的求解过程中的应用。通过这一环节，学生们牢牢地掌握了这块知识。

从我近二十年的教学效果来看，只要在学习的过程中，能踏踏实实做到：课前引导学生根据“知识预览”做好预习，课堂上实行小组合作的教学方式，课后组织学生参加阶段性的小课题研究，就有助于学生自主学习能力的培养，就能大幅度地提高数学成绩。教师应根据学生的实际情况，充分调动学生的学习积极性，培养学生的自主学习能力，只有这样，才能做到教与学的结合，提高学生的的综合素质。这正是高中数学新课程改革所要求的。

[1]刘泽斌.新课程背景下高中数学反思性教学探析[J].教育教学论坛，2012(36)：108-109.

[2]裴瑞芝.浅谈初中数学教学中学生自主学习能力的培养[D].学周刊：C 2012(8)：26-30

[3]董林伟.立体几何中角与距离的计算[J].中学数学月刊，1997(4)：20-23.