一类求解形如|Am+Bn|+|Cm+Dn|最大值的转化策略

☉湖北大学附属中学 李 俊

在教学过程中，我们不乏发现：大型调考试题往往源于教材，又高于教材，很好地模拟了高考试题，有下面两个例子.

例1 （2017年浙江卷）已知向量a，b满足|a|=1，|b|=2.则|a+b|+|a-b|的最小值为________，最大值为________.

解析：设a=（cosα，sinα），b=（2cosβ，2sinβ）.

所以a+b=（cosα+2cosβ，sinα+2sinβ），

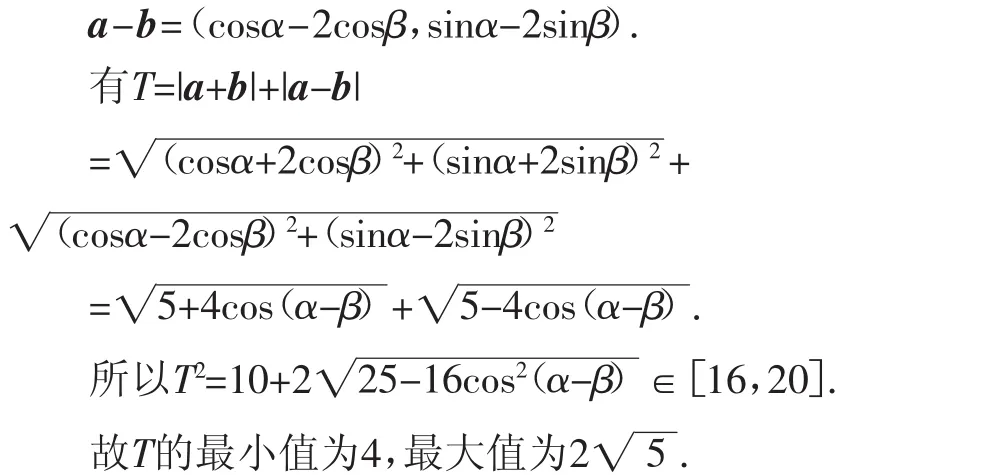
例2 （2017年武汉市二月调考）已知m，n为非零向量，且满足|m|=2，|m+2n|=2.则|2m+n|+|n|的最大值为（ ）.

比较以上两例可以看到，利用线性代换、向量模的意义及坐标表示，圆的参数方程等知识，结合柯西不等式，得到了已知|A′m+B′n|=r，|C′m+D′n|=t，求|Am+Bn|+|Cm+Dn|的最大值问题的转化策略.F