构造函数，巧解题

☉辽宁省沈阳市第四中学 孙玉才

若题设出现与导数有关的不等式，或题设给出“双变量”不等式恒成立，则往往可通过构造函数，借助导数知识获得简捷、明了的解答.请看以下归类解析.

一、考虑移项作差，构造函数

评注：本题构造函数之后，需要先利用导数研究函数的单调性，再利用所得函数的单调性求解不等式.

变式训练：已知函数f（x）的定义域为R，满足f（-2）=2018，且对任意x∈R，都有f′（x）＞2x成立，则不等式f（x）＞x2+2014的解集为________.

简解：令函数F（x）=f（x）-x2-2014，则F′（x）=f′（x）-2x＞0，所以F（x）在R上为增函数.又可求得F（-2）=0，所以f（x）＞x2+2014⇔F（x）＞0=F（-2）⇔x＞-2.故所求不等式的解集为（-2，+∞）.

二、直接考虑导数运算法则，构造函数

故所求不等式的解集为（1，+∞）.

评注：本题求解的关键是根据不等式f（x）＞xf′（x），考虑导数的运算法则，灵活构造函数；构造函数之后，应充分利用函数的性质求解目标问题.

变式训练：已知f（x）是定义在（0，+∞）上的非负可导函数，且满足xf′（x）+f（x）≤0.对任意正数a，b，若a＜b，则必有（ ）.

（A）af（b）≤bf（a）

（B）bf（a）≤af（b）

（C）af（a）≤f（b）

（D）bf（b）≤f（a）

简解：令函数y=xf（x），x∈（0，+∞）.由于xf′（x）+f（x）≤0，故函数y=xf（x）单调递减或为常数函数.所以，必有af（a）≥bf（b）.又根据f（x）≥0，且0＜a＜b，可得af（a）≤bf（a），af（b）≤bf（b）.综上，af（b）≤bf（b）≤af（a）≤bf（a）.故选A.

三、结合特殊的指数函数y=ex，考虑导数运算法则，构造函数

例3已知f（x）为定义在（-∞，+∞）上的可导函数，且f（x）＞f′（x），则（）.

（A）f（2）＞e2·f（0），f（100）＞e100·f（0）

（B）f（2）＜e2·f（0），f（100）＞e100·f（0）

（C）f（2）＞e2·f（0），f（100）＜e100·f（0）

（D）f（2）＜e2·f（0），f（100）＜e100·f（0）

解析：因为（fx）＞f（′x），考虑特殊的指数函数y=ex，可构造函数，则，所以函数F（x）为（-∞，+∞）上的减函数.

变式训练：设函数（fx）的定义域为R，且对任意x∈R，f（′x）+（fx）＞0，则对任意正数a，必有（ ）.

简解：令函数F（x）=exf（x），则F′（x）=ex［f′（x）+f（x）］＞0，故F（x）在R上单调递增.又a＞0，所以F（a）＞F（0），即eaf（a）＞e0f（0），所以.故选C.

四、考虑外在结构特征，构造函数

例4设函数f（x）=x3-11x，若对任意a，b∈（2m，m+1），且b＞a，有不等式恒成立，则实数m的取值范围是_________.

构造函数h（x）=f（x）-x=x3-12x，

则h（x）在（2m，m+1）上单调递减.

又由h′（x）=3x2-12=3（x+2）（x-2）知，

函数h（x）的单调递减区间为（-2，2）.

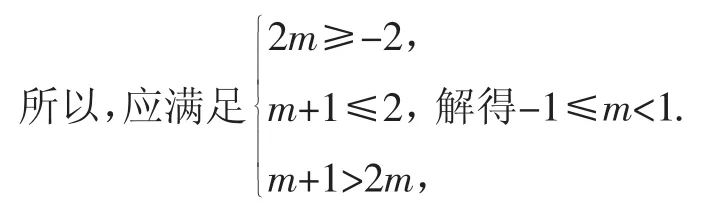
故实数m的取值范围是［-1，1）.

评注：本题切入点的探求具有一定的隐蔽性，需要灵活变形.构造函数之后，要注意借助定义、导数均可分析函数的单调性，并活用之解题.

综上，构造函数是一种创新思维，对能力的要求较高，需要我们在解题实践中不断积累经验，且学且悟且应用.