OFDM系统中利用循环前缀的非迭代相位噪声抑制算法

袁建国，张锡若邱飘玉，王 永，庞 宇，林金朝

(1.重庆邮电大学 光电信息感测与传输技术重庆市重点实验室，重庆 400065;2.重庆邮电大学 光通信与网络重点实验室,重庆 400065)

0 引 言

近年来正交频分复用(OFDM)技术被广泛地应用于宽带无线通信系统中，是下一代移动通信的核心技术。OFDM技术的优点在于它可以有效地对抗多径时延引起的符号间干扰，具有很高的频谱利用率[1,2]。但由于OFDM符号周期较长，对子载波之间的正交性要求比较严格，从而对相位噪声极为敏感。

相位噪声对OFDM系统造成的影响主要有两方面，由相位噪声的零阶频谱分量引起的公共相位误差(Common phase error，CPE)和非零阶频谱分量引起的载波间的干扰(Inter-carrier interference，ICI)[3-6]。目前，已有不少学者相继提出了许多算法来抑制相位噪声对OFDM系统的影响。文献[7，8]利用直接判决对相位噪声进行抑制，文献[7]不需要额外的导频信息来对相位噪声进行抑制，频谱利用率比较高，但该算法只有当CPE足够小不会引起错误判决时DDPE (Decision-directed phase equalization)很有效。当调制阶数较高时，即使很小的相位旋转也会导致判决错误，对相位噪声的抑制有限。文献[8]克服了直接判决相位噪声抑制算法在阶数较高时的限制问题，先通过一个盲自适应过程对高阶星座调制中的CPE进行抑制，再通过直接判决对相位噪声进行进一步的抑制。但该算法的主要是对CPE进行抑制，当相位噪声较大时，抑制效果较差。文献[9]通过在发送端采用有限的状态量来近似表示相位噪声，对维纳相位噪声进行编码，然后在接收端使用增强接收信号的模型来估计编码系数以及其他参数。文献[10-12]提出基于时域分块盲估计ICI，该算法将接收到的OFDM符号分割为几个子符号，用每个子符号上的相位噪声估计值来消除ICI，最后利用导频或者改进的伪导频来补偿残余的CPE和ICI 对系统的影响，但是子符号的增加会大大增加计算复杂度。在文献[13]中提出了一种非迭代的基于线性内插的ICI抑制算法，该算法通过对相邻OFDM符号中相位噪声的相角进行线性内插来拟合相位噪声，但由于每个OFDM符号中只有一个插值点，当相位噪声线宽较大时，OFDM符号中的相位噪声会有比较大的起伏，此时采用该算法得到的相位噪声估计值无法准确估计实际的相位噪声。

针对这一问题，本文提出了一种非迭代的利用循环前缀进行线性内插的相位噪声抑制算法，该算法利用循环前缀与OFDM符号的相关性，增加了OFDM符号内的有效数据，通过对原有的插值点进行优化，增加了线性内插中的插值点数，使得估计出的相位噪声更加贴近实际的相位噪声，在相位噪声较大时，也有较好的抑制性能。

1 相位噪声的模型

受相位噪声影响的OFDM系统基本框图如图1所示，发送的时域信号x(n)在传输时受到相位噪声和高斯白噪声的影响，其中相位噪声表现为对发送信号的乘性干扰，高斯白噪声为加性干扰。在接收端，接收信号y(n)为

y(n)=x(n)⊗h(n)ejφ(n)+w(n)

(1)

φ(n)=φ(n-1)+Δφ

(2)

图1 OFDM系统框图Fig.1 Block diagram of OFDM systems

式中：在实际中，初始条件φ(0)=0；Δφ表示相邻两采样点之间的相位噪声增量；Δφ～(0,2πΔf/fs)，其中Δf为相位噪声的洛伦兹功率谱密度的双边带3 dB线宽，fs表示模数变换采样频率。

假设接收端理想同步，经过FFT变换后的频域信号为:

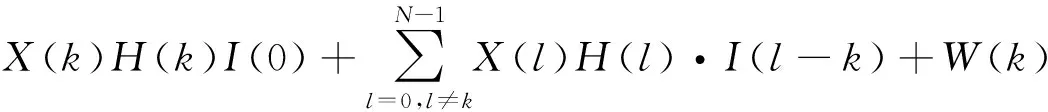
(3)

式中：W(k)和I(k)分别为高斯白噪声和的相位噪声的频域形式；H(k)为信道频域响应。

(4)

由式(4)可知，相位噪声对OFDM符号的影响有两部分，第一部分为公共相位误差I(0)，它是由相位噪声的直流分量引起，对同一个OFDM符号中所有的子载波的影响相同；第二部分为子载波间干扰I(k),k=1,2,…，N-1，它是由相位噪声的高频成分引起的，对同一个OFDM符号的不同子载波影响是不同的。

2 算法原理

2.1 基于CPE的线性内插算法

(5)

(6)

2.2 循环前缀与OFDM符号的对应关系

OFDM符号长度为N，循环前缀长度为Ng，在发送端，第m个OFDM符号中的循环前缀与尾部采样点的对应关系可表达为:

xm(n)=xm(N+n)

(7)

1≤n≤Ng

受到相位噪声的影响，接收端的信号对应为

(8)

1≤n≤Ng

式(8)说明在一个OFDM符号内，未受信道影响的循环前缀与OFDM符号尾部对应采样点之间存在一个相位差，该相位差可表示为:

(9)

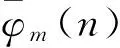
(10)

2.3 改进的利用循环前缀进行插值的相位噪声抑制算法

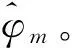
当进行线性插值时，每个OFDM符号的第Ng个采样点与第N+Ng个采样点的相位噪声估计值可表示为:

(11)

(12)

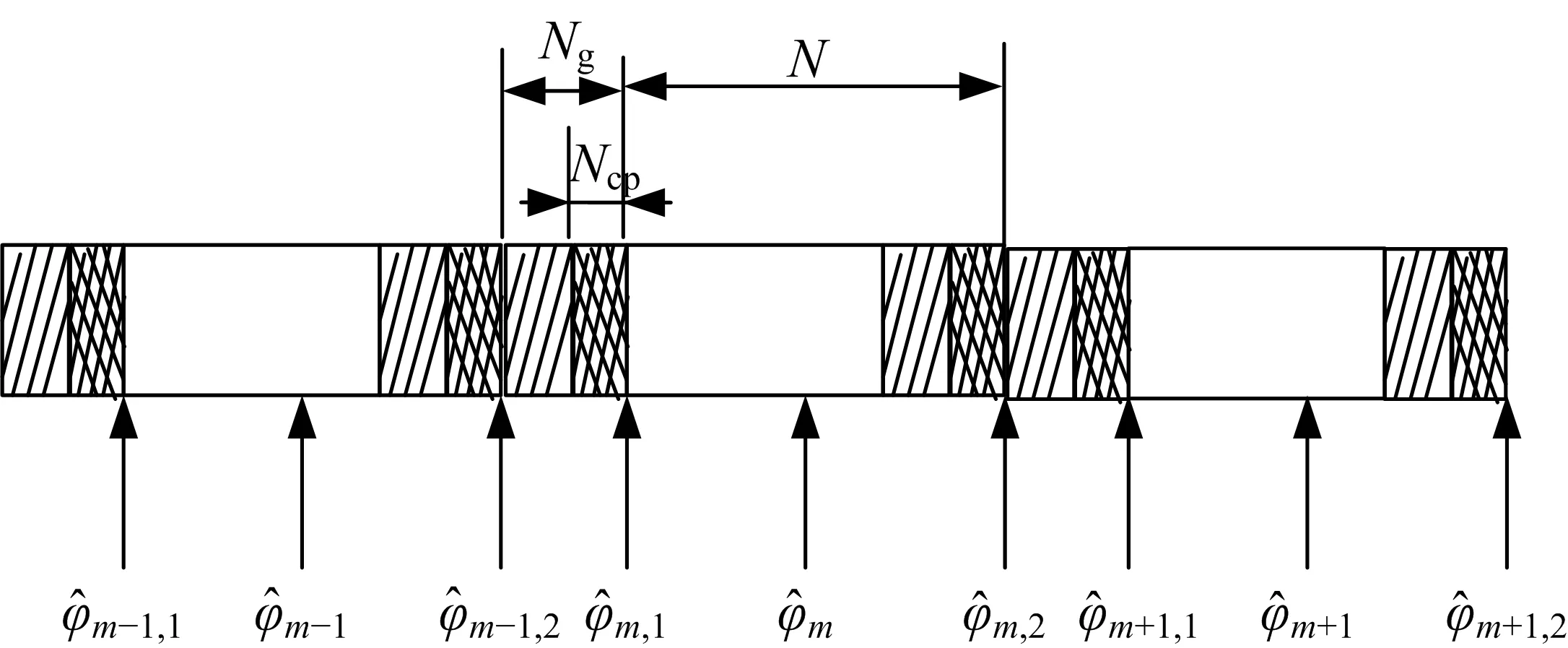
图2 线性内插插值点的位置Fig.2 Location of interpolation points

(13)

3 仿真分析

通过仿真来分析本文所提出的利用循环前缀进行线性插值的相位噪声抑制算法，同时与文献[13]提出的算法进行对比。文献[13]中的算法标记为LI-CPE，本文算法标记为CP-LI-CPE。系统的参数设置如下：OFDM的子载波数N=128，循环前缀的长度Ng=N/8=16，导频数量为16，模数变换的采样频率fs=20 MHz，OFDM符号个数为5000，系统调制采用16QAM格式。

图3为相位噪声线宽分别为0.5、1、2 kHz，参与算法的循环前缀个数Ncp为2的情况下，两种算法的误码率曲线图。

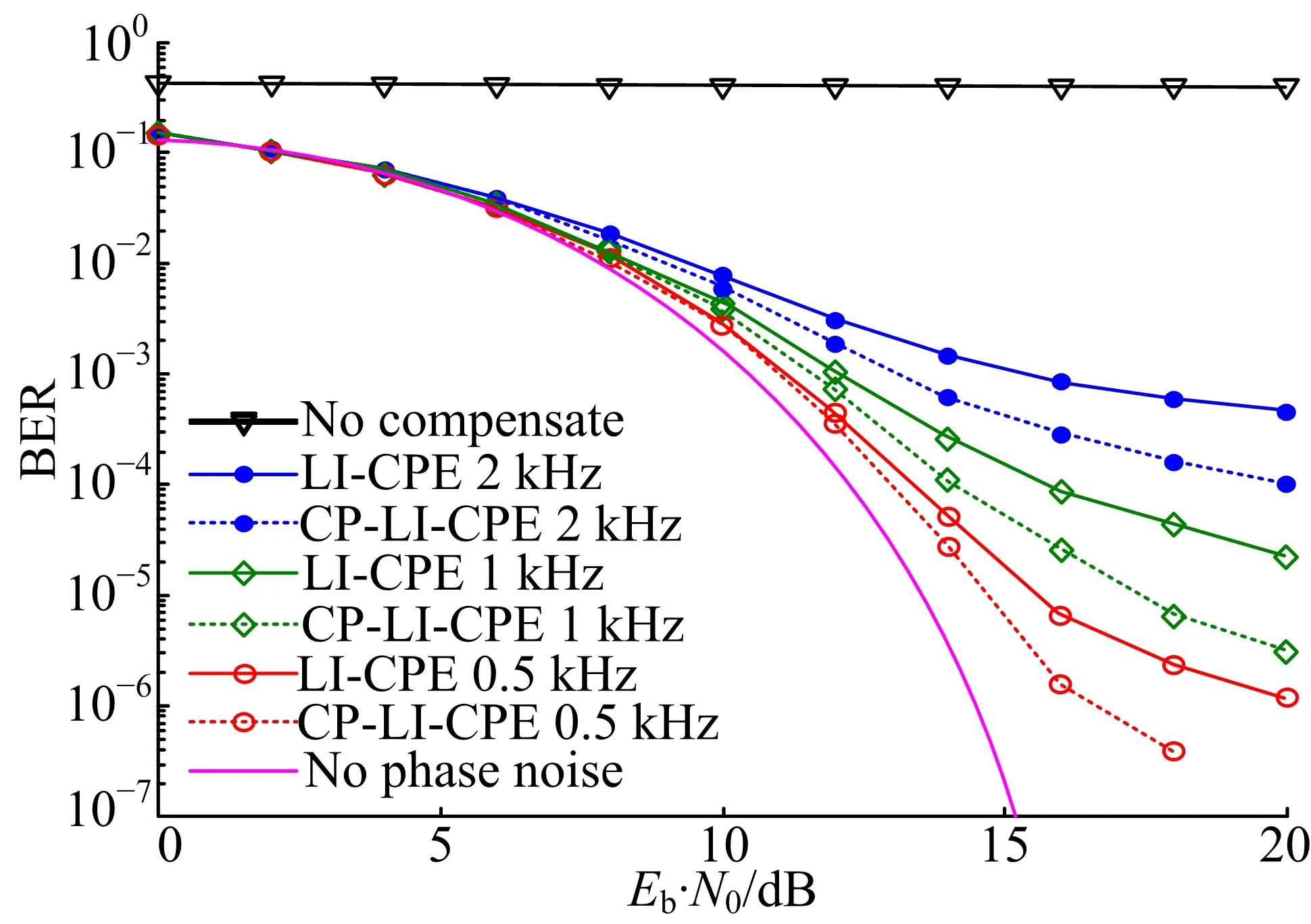
图3 LI-CPE与CP-LI-CPE在不同相位噪声线宽下的误码率性能Fig.3 BER performance of LI-CPE algorithm andCP-LI-CPE algorithm under different phasenoise linewidths

由图3可知，在相位噪声线宽为500 Hz，误码率(BER)为10-5时，CP-LI-CPE算法相比LI-CPE算法的信噪比增益约为0.8 dB，并且该算法的误码率曲线比较贴近无相位噪声曲线，说明CP-LI-CPE算法在该相位噪声线宽下对相位噪声的消除效果比较明显。在相位噪声线宽为1 kHz，误码率为10-4时，CP-LI-CPE算法相比LI-CPE算法的信噪比增益约为1 dB，并且有效地降低了错误平层。在相位噪声线宽为2 kHz，误码率为10-3时，CP-LI-CPE算法相比LI-CPE算法的信噪比增益约为1.8 dB，LI-CPE算法已经出现了严重的错误平层，而CP-LI-CPE算法在一定程度上降低了错误平层。这说明了CP-LI-CPE算法在相位噪声线宽较大时,能够有效清除相位噪声。

图4给出了相位噪声线宽为2 kHz，CP-LI-CPE算法在参与算法的循环前缀个数分别为1、2、3、4的情况下系统误码率与信噪比的关系图。

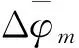
图4 CP-LI-CPE算法在不同循环前缀个数下的误码率性能Fig.4 BER performance of CP-LI-CPE algorithmunder different CP numbers

图5给出了相位噪声线宽为2 kHz时，CP-LI-CPE算法与文献[13]中的LI-CPE算法所估计出的相位噪声的插值对比图。

图5 CP-LI-CPE算法与LI-CPE算法的时域内插对比图Fig.5 Time domain interpolation contrast figure ofLI-CPE algorithm and CP-LI-CPE algorithm

由图5可知，通过增加每个OFDM符号中的内插点的个数，本文算法得到的相位噪声估计曲线更能拟合实际的相位噪声。

4 结束语

针对OFDM系统中相位噪声的抑制问题，本文提出了一种非迭代的利用循环前缀进行线性内插的相位噪声抑制算法。该算法利用循环前缀与OFDM符号后半段的固有属性，只利用少量的循环前缀信息，即可通过增加每个OFDM符号内线性插值的插值点数，使得线性插值得到的相位噪声估计曲线更加拟合于实际的相位噪声曲线。仿真结果表明：与文献[13]中的线性插值算法相比，本文算法能够有效地抑制CPE和部分的ICI干扰，提升了0.8～1.8 dB的信噪比增益，降低了错误平层。但在相位噪声线宽较大时，该算法提升的性能有限，因此在下一阶段的研究中，可以将该算法与其他ICI抑制算法结合起来，对残余的ICI进行进一步的抑制。

[1] 崔金, 张波, 张彦仲. 基于伪随机后缀的OFDM信道估计方法[J]. 吉林大学学报：工学版, 2014, 44(1): 253-258.

Cui Jin, Zhang Bo, Zhang Yan-zhong. OFDM channel estimation based on pseudo random postfix [J]. Journal of Jilin University(Engineering and Technology Edition), 2014,44(1):253-258.

[2] Iqdour Radouane, Jabrane Younes. Wavelet networks for reducing the envelope fluctuations in WirelessMan-OFDM systems [J]. Digital Communications and Networks, 2016, (2):77-83.

[3] Mathecken P, Riihonen T, Werner S, et al. Performance analysis of OFDM with Wiener phase noise and frequency selective fading channel [J]. IEEE Transactions on Communications, 2011, 59(5): 1321-1331.

[4] Lin K Y, Lin H P, Tseng M C. An equivalent channel time variation mitigation scheme for ICI reduction in high-mobility OFDM systems [J]. IEEE Transactions on Broadcasting, 2012, 58(3): 472-479.

[5] Tchamov N N, Rinne J, Hazmi A, et al. Enhanced algorithm for digital mitigation of ICI due to phase noise in OFDM receivers [J]. IEEE Wireless Communications Letters, 2013, 2(1): 6-9.

[6] 李玲香，李季碧. CO-OFDM系统中基于线性预处理的新相位噪声抑制算法[J]. 重庆邮电大学学报:自然科学版，2016, 28(5):743-748

Li Ling-xiang, Li Ji-bi. Novel phase noise suppression algorithm based on the linear preprocessing in CO-OFDM systems [J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2016, 28(5):743-748.

[7] Mousa-Pasandi M E, Plant D V. Zero-overhead phase noise compensation via decision-directed phase equalizer for coherent optical OFDM [J]. Optics Express, 2010, 18(20): 20651-20660.

[8] Ha Y, Chung W. Non-data-aided phase noise suppression scheme for CO-OFDM systems [J]. IEEE Photonics Technology Letters, 2013, 25(17): 1703-1706.

[9] Negusse S, Zetterberg P, Handel P. Phase-noise mitigation in OFDM by best match trajectories [J]. IEEE Transactions on Communications, 2015, 63(5): 1712-1725.

[10]Lee M K, Lim S C, Yang K. Blind compensation for phase noise in OFDM systems over constant modulus modulation [J]. IEEE Transactions on Communications, 2012, 60(3): 620-625.

[11]Cao S,Kam P Y, Yu C. Time-domain blind ICI mitigation for non-constant modulus format in CO-OFDM [J]. IEEE Photonics Technology Letters, 2013, 25(24): 2490-2493.

[12]Liu Y, Yang C, Li H. Cost-effective and spectrum-efficient coherent TDM-OFDM-PON aided by blind ICI suppression [J]. IEEE Photonics Technology Letters, 2015, 27(8): 887-890.

[13] Mousa-Pasandi M E, Plant D V. Noniterative interpolation-based partial phase noise ICI mitigation for CO-OFDM transport systems [J]. IEEE Photonics Technology Letters, 2011, 23(21): 1594-1596.