基于等效晃动模型的液罐车防侧翻控制策略

赵伟强，封 冉，宗长富

(吉林大学 汽车仿真与控制国家重点实验室，长春 130022)

0 引 言

随着中国道路交通的迅速发展，利用液罐车运输液体危化品所占的比例越来越大。液罐车具有吨位大、质心高的特点，同时由于罐内液体的流动特性，当液罐车在弯道行驶或紧急避障时，车辆状态的改变会使液体对罐壁产生冲击，从而进一步降低液罐车的行驶稳定性，易使其发生侧翻事故，进而导致危化品的泄漏、燃烧甚至爆炸，不但造成大量人员伤亡、财产损失并且严重污染环境。

目前，针对液罐车的研究主要集中于罐内液体晃动的动力学机理分析、罐体结构的优化等。文献[1]运用流体体积(VOF)法对非满载液罐车在极限工况时罐内液体晃动动力学特性进行数值模拟，并分析了液罐内防波板数量、结构以及充液比等影响因素。文献[2，3]研究了椭圆形截面液罐车罐体几何尺寸对整车侧倾稳定性的影响，得出液罐车所受罐内液体冲击力及力矩最小时的长轴与短轴比例值及具体尺寸。液罐结构优化能在一定程度上提高其稳定性，但其效果远不如对车辆应用主动控制策略[4-7]。

液罐车动力学模型需兼顾准确性及计算速度，液体晃动简化模型主要包括准静态模型以及等效机械模型[8-10]，其中准静态模型中不包含液体的晃动，然而等效机械模型既考虑了车辆侧倾时液体质心偏移产生的侧倾力矩，又考虑了液体对罐体壁面的冲击效应[11-15]。

针对目前提高液罐车稳定性的方法以及液罐车模型两方面的不足，本文建立了液罐车等效晃动动力学模型，并提出基于差动制动的液罐车防侧翻控制策略；通过Trucksim/Simulink联合仿真，验证了液体晃动对车辆运动的影响以及防侧翻控制策略的有效性。

1 液罐车动力学模型

本文的研究对象为单车式液罐车且罐体为矩形，装载货物为煤油，车辆侧视图、俯视图及后视图如图1～图3所示。

图1 液罐车侧视图Fig.1 Left view of tank truck

图2 液罐车俯视图Fig.2 Top view of tank truck

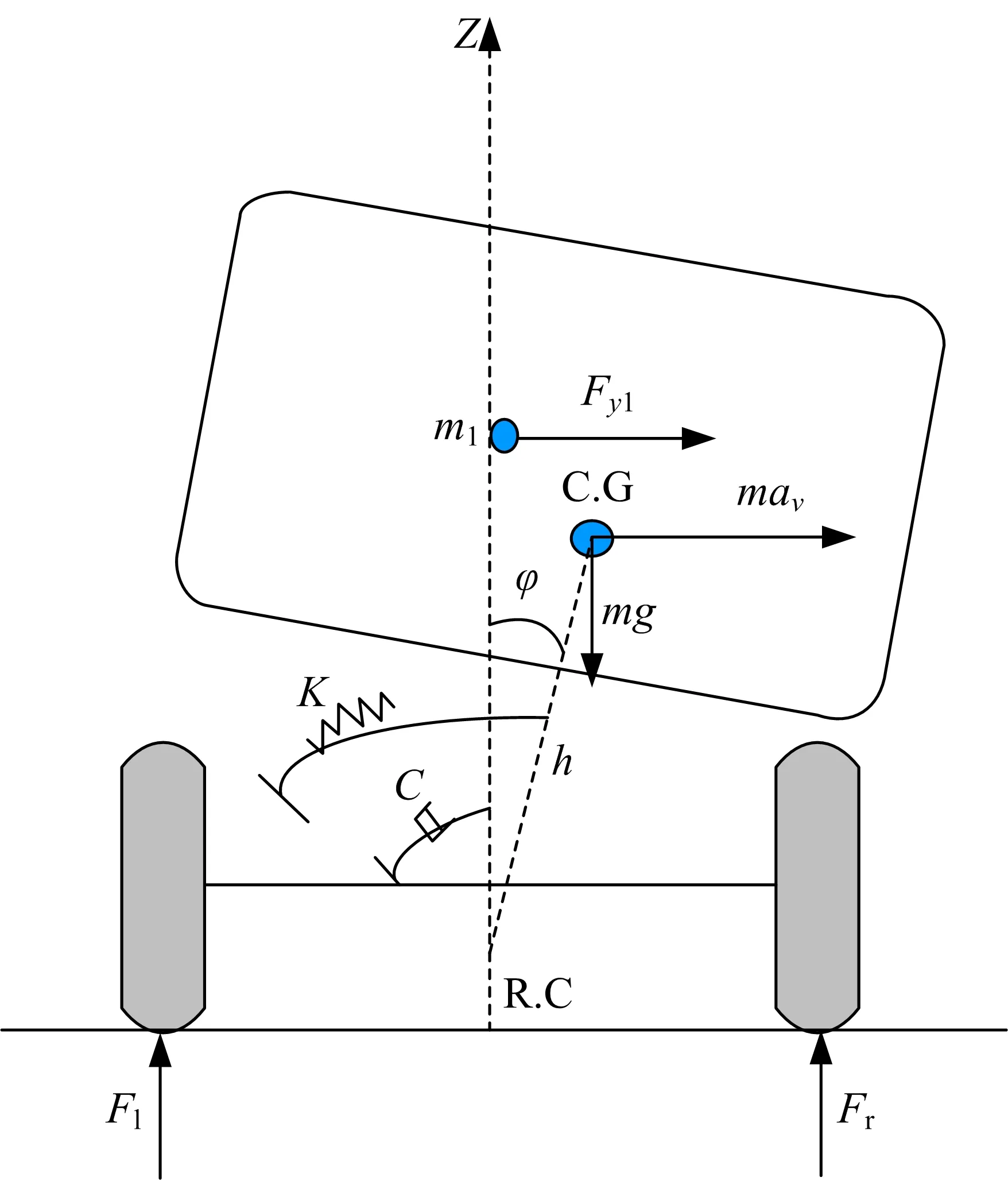
图3 液罐车后视图Fig.3 Rear view of tank truck

在部分充液情况下，液罐内液体在车辆运动的激励下将产生对液罐壁面的冲击力，进而影响车辆的运动状态，冲击力的大小可用来表征液体晃动的剧烈程度。

1.1 液罐车车体部分动力学模型

本文采用3自由车辆模型，包括车辆侧向、横摆和侧倾运动，在建立动力学模型时，需要对实际车辆作如下假设：①模型以前轮转角作为输入；②汽车在水平路面行驶，忽略车辆的垂直运动；③不考虑车辆的俯仰运动；④忽略空气动力的作用；⑤忽略左、右轮胎由于载荷的变化引起轮胎特性的变化以及轮胎回正力矩作用。

根据达朗伯原理，可对液罐车车体部分建立动力学平衡方程。

沿y轴力平衡式：

(1)

绕z轴横摆力矩平衡式：

(2)

绕x轴侧倾力矩平衡式：

(3)

式中：Fyl表示液体晃动对罐壁的冲击力；hFyl为冲击力作用点到侧倾轴线的距离，由双向耦合关系知，两值可由液体晃动模型求解得到。

1.2 液体晃动等效模型

目前，针对储液罐内液体晃动现象的冲击动力学研究方法主要有：数值模拟法、机械动力学等效法和物理试验法。其中数值模拟法求解过程复杂，物理实验法试验要求高、危险性较大，为保证模型计算的实时性，通常将液体晃动问题等效为机械模型。由于单摆模型可有效反映液体在横向激励中的晃动特性，因此本文采用单摆模型描述罐内液体运动。

液体晃动单摆模型示意图如图4所示，其中液体质量分为固定质量mo及等效单摆质量mp两部分，固定质量质心位于距罐底部ho处，单摆质量位于距罐底部hp处。

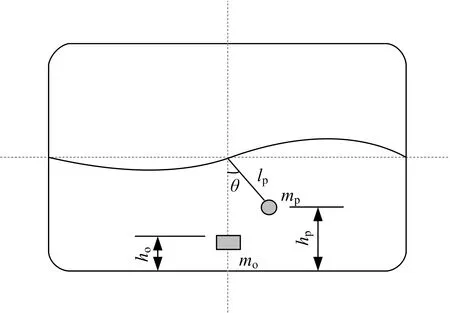
图4 等效单摆模型示意图Fig.4 Equivalent pendulum model

具体计算公式如下：

ml=ρhsed

(4)

(5)

mo=ml-mp

(6)

(7)

(8)

式中：hs为罐内液体深度；e、d分别为罐体的长与宽。

单摆模型可近似看做系于液罐中心处，即所有的旋转被认为在该点附近发生，因此，罐体的中心和单摆质量之间的距离可以被认为是等效摆长lp。液体的固有频率与等效摆长有关，计算公式如下：

(9)

单摆模型的动力学方程和横向激励产生的晃动力以及液体晃动对罐底的力矩计算方程如下：

(10)

(11)

M=Fylhp+mpglpθ

(12)

式中：θ为等效摆角；cl为液体等效阻尼系数。

2 防侧翻控制策略

2.1 预警指标

判定车辆是否会发生侧翻，目前应用比较广泛的是横向载荷转移率法，横向载荷转移率(LTR)是指车辆两侧车轮上的垂直载荷之差与垂直载荷之和的比值，具体表达式如下：

(13)

式中：Fzl和Fzr分别为车辆左、右车轮上的垂直载荷。

在极限工况下，若一侧车轮抬起脱离地面，此时LTR为-1或1，因而该值可反映车辆的侧倾稳定性。由于左、右车轮垂直载荷不易直接测量，所以本文采用其等效表达式：

(14)

式中：C、K分别为悬架阻尼与刚度值；φ为车辆侧倾角；T为车辆轮距。

2.2 制动轮缸压力决策

本文基于差动制动设计防侧翻控制策略，当预警模块检测到车辆将要侧翻时，激活防侧翻控制模块，根据实际侧倾角与理论侧倾角的偏差求得补偿横摆力矩值，进而求得制动轮轮缸压力值，从而防止车辆侧翻。本文采用PID算法，补偿横摆力矩计算框图如图5所示。

φt为经3自由度液罐车模型计算得到的理想侧倾角值，φa为来自Trucksim的实际车辆侧倾角，eφ为二者的偏差值。补偿横摆力矩具体计算公式如下：

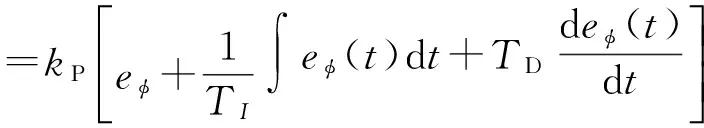
(15)

式中：kP为比例系数；TI是积分时间常数；TD是微分时间常数。

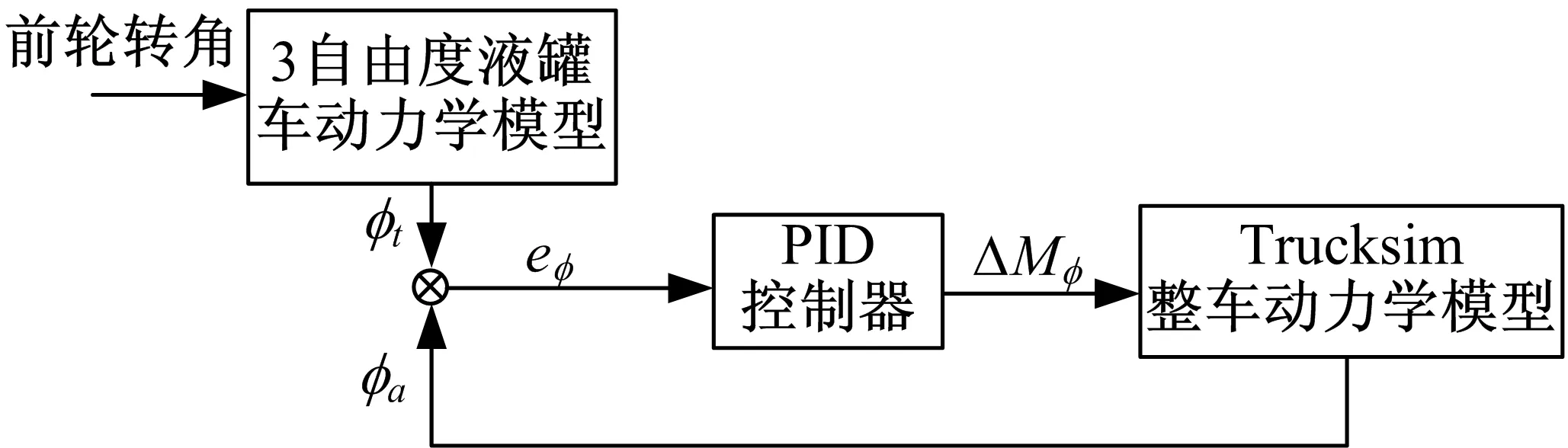
图5 补偿横摆力矩计算框图Fig.5 Calculation of additional yaw moment

能够提供有效补偿横摆力矩的车轮有前轮和后外轮，但每个车轮效率不同，本文选择车辆前轮作为制动轮。LTR数值可以反映车辆的转向状态，现制定制动车轮决策规则如下：若LTR∈[-1,0)，表示车辆向左侧转弯，此时选择右前轮作为制动轮；同理，若LTR∈(0,1]，选择左前轮作为制动轮。

制动轮缸压力计算公式如下：

(16)

式中：ΔP定义为轮缸所需压力；ΔMφ定义为根据侧翻控制策略计算得出的附加横摆力矩；Rw为车轮半径；Sc为制动气室有效作用半径；Rc为制动器的有效作用半径；L为决策车轮到车辆质心位置的距离。

3 仿真分析

本文中，首先比较相同工况下，车辆在装载等质量的液体货物与固体货物时的运动状态，以确认液体晃动对车辆侧倾稳定性的影响。其次，当发现液罐车具有侧翻危险时，对车辆进行差动制动主动防侧翻控制，通过比较控制前、后的液罐车状态值来证明防侧翻控制策略的有效性。

3.1 液体晃动对车辆运动状态的影响

为确认液体晃动对车辆响应的影响，本文选择阶跃工况进行仿真分析，比较了当车速分别为40 km/h与70 km/h时，装载相同质量的固体货物与液体货物的车辆侧向加速度、横摆角速度以及侧倾角。

阶跃转向的方向盘转角为180°，转角增大时间为0.66 s，如图6所示。

由图7～图9可知，在低速行驶时，由于罐内液体的晃动，液罐车的侧向加速度、横摆角速度、给定阶跃工况下，车速为40 km/h时的仿真曲线如图7所示。

图6 方向盘阶跃转角Fig.6 Step input of steering wheel angle

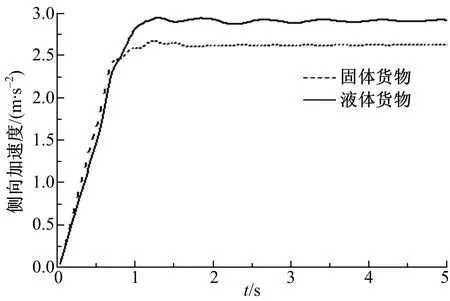
图7 侧向加速度时间历程Fig.7 Lateral acceleration

图8 横摆角速度时间历程Fig.8 Yaw rate

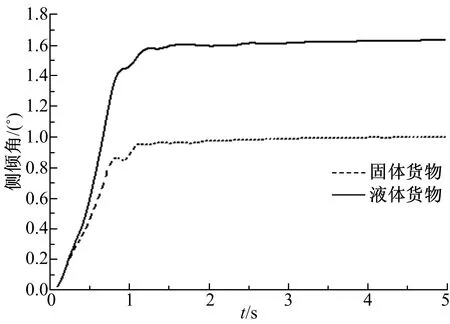
图9 侧倾角时间历程Fig.9 Roll angle

侧倾角明显大于装载等质量固体货物车辆的对应值，即液罐车稳定性明显较低。

相同阶跃工况下，当车辆速度均达到70 km/h时，仿真结果如图10所示，装载固体货物的车辆侧倾角保持在3°以内，而液罐车侧倾角在2.5 s左右达到76°，即液罐车发生侧翻。

图10 70 km/h时侧倾角Fig.10 Roll angle under 70 km/h

3.2 防侧翻控制

为证明防侧翻控制策略的有效性，针对上述阶跃工况下，车速为70 km/h的液罐车进行防侧翻控制。仿真结果如图11所示，在4 s左右液罐车侧倾角降至2.3°，随后保持稳定，即在本文控制策略作用下车辆未发生侧翻。

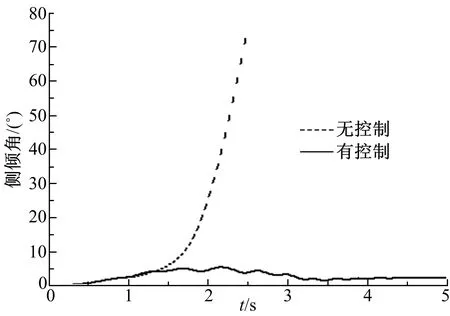
图11 阶跃工况有、无控制策略时侧倾角比较Fig.11 Roll angle comparison in step condition

液罐车在50 km/h、鱼钩工况下方向盘转角为±294°，转角增大时间为0.4 s，如图12所示。此外，本文还比较了在50 km/h、鱼钩工况下有无控制时的侧倾角、侧向加速度、液体晃动力，分别如图13～图15所示。

图13、图14表明，若不采取任何安全措施，液罐车在3.5 s左右发生侧翻；然而，由图15可知，在主动防侧翻控制策略作用下，液体晃动力可从最大峰值17 kN降低至3.5 kN，并最终维持稳定，液罐车侧倾角及侧向加速度可保持在安全范围内，即该策略有效地提高了液罐车的侧倾稳定性。

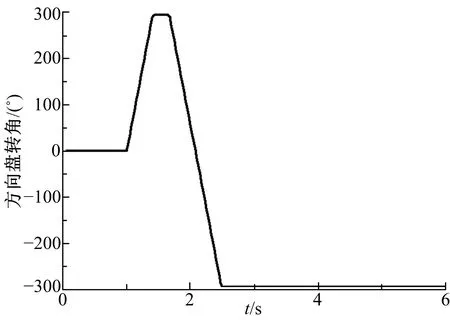
图12 方向盘转角Fig.12 Steering wheel angle in fishhook condition

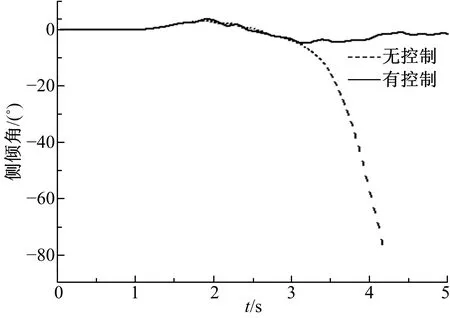
图13 鱼钩工况时侧倾角Fig.13 Roll angle in fishhook condition

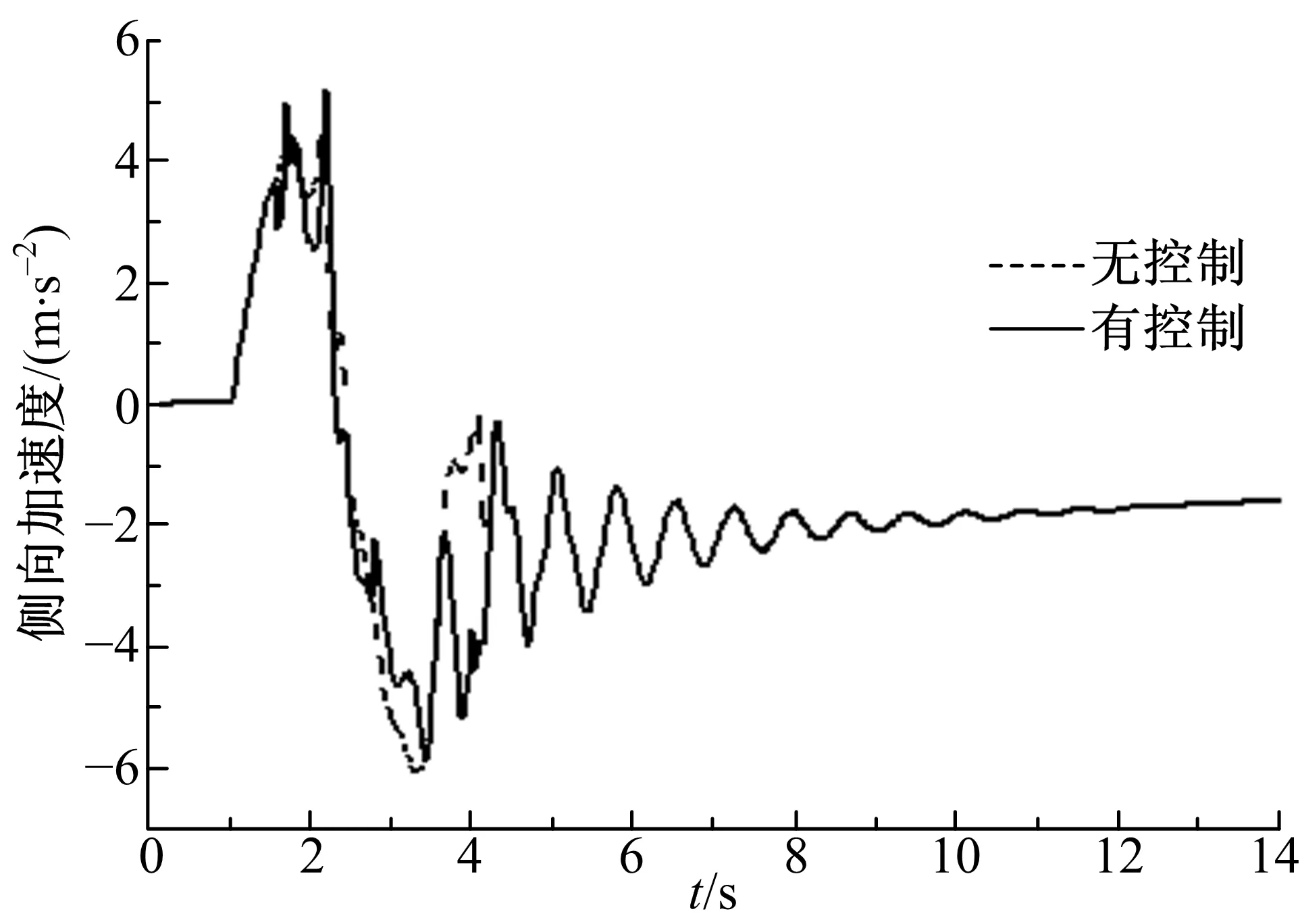
图14 鱼钩工况时侧向加速度Fig.14 Lateral acceleration in fishhook condition

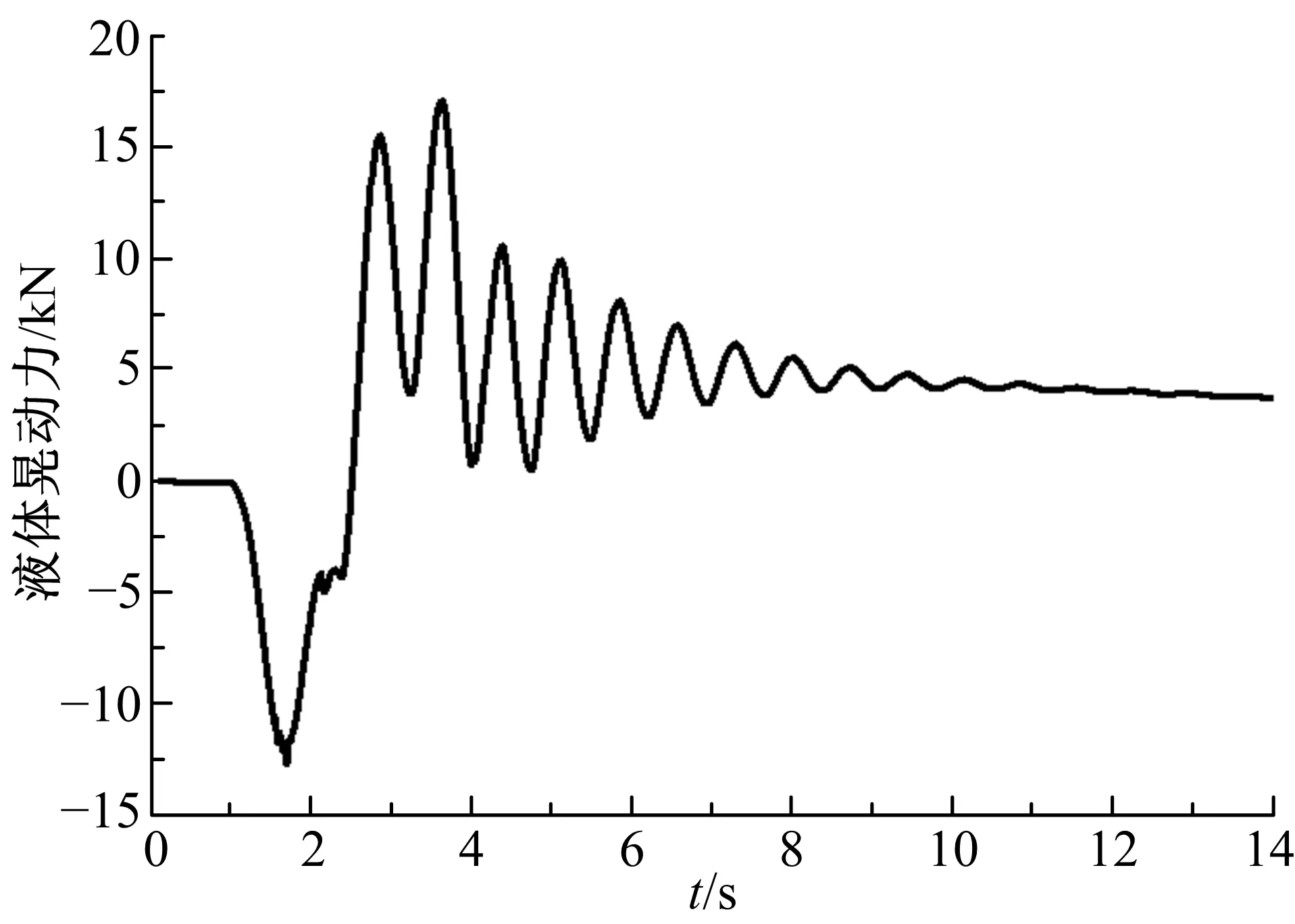
图15 鱼钩工况时液体晃动力Fig.15 Sloshing force in fishhook condition

4 结束语

本文基于等效晃动模型对液罐车防侧翻控制策略进行了研究。利用等效单摆模型模拟矩形液罐内液体的横向晃动，并将该模型与3自由度车辆模型集成，建立了液罐车等效晃动动力学模型；验证了阶跃转向工况下，液罐内液体晃动对车辆侧向稳定性的影响；选取横向载荷转移率为侧翻指标并利用差动制动方法，验证了本文防侧翻控制策略在阶跃工况及鱼钩工况下的有效性。本文方法对于提高液罐车行驶稳定性，减少侧翻事故具有一定的理论意义。

[1] 赵树恩，赵灵鹤. 汽车罐车横向运动液体晃动动力学特性模拟[J]. 应用数学和力学，2014，35(11)：1259-1270.

Zhao Shu-en,Zhao Ling-he.Dynamic Simulation of liquid sloshing characteristics for tank trucks in lateral movement [J]. Appllied Mathematics and Mechanics,2014,3(11):1259-1270.

[2] 于迪，李显生，刘宏飞，等. 非满载液罐车侧倾稳定性模型研究[J]. 湖南大学学报：自然科学版，2016，43(8)：40-44.

Yu Di, Li Xian-sheng, Liu Hong-fei，et al. Research on roll stability model of partially-filled tankers [J]. Journal of Hunan University (Natural Sciences), 2016, 43(8): 40-44.

[3] 李显生，于迪，张海景. 基于遗传算法的液罐车侧倾稳定性模型[J]. 中国公路学报，2015，28(7)：115-120.

Li Xian-sheng, Yu Di, Zhang-hai Jing. Roll stability model of tank truck based on genetic algorithm [J]. China Journal of Highway and Transport, 2015, 28(7):115-120.

[4] Avesta Goodarzi. Integrated yaw and roll moments control of articulated vehicles [C]∥SAE Paper, 2009-01-2874.

[5] Yoon Jang-yeol, Kim Dong-shin. Design of a rollover index-based vehicle stability control scheme [J]. Vehicle System Dynamics, 2007, 45(5): 459-475.

[6] 李显生，郑雪莲，刘宏飞. 非满载罐式半挂汽车列车侧倾稳定性评价改进算法[J]. 吉林大学学报:工学版，2012，42(5):1089-1094.

Li Xian-sheng,Zheng Xue-lian, Liu Hong-fei. Improved algorithm on roll stability evaluation of partially filled tractor-tank semitrailer [J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(5): 1089-1094.

[7] Acarman T, Ozguner U. Rollover prevention for heavy trucks using frequency shaped sliding mode control [J]. Vehicle System Dynamics, 2006, 44(10): 737-762.

[8] 胡晓明，李万莉，孙丽，等. 液体晃动降低半挂液罐车行驶稳定性[J]. 农业工程学报，2013，29(6)：49-58.

Hu Xiao-ming, Li Wan-li, Sun Li, et al. Liquid sloshing reduces driving stability of semi-trailer liquid tank [J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(6): 49-58.

[9] 岳宝增，祝乐梅，于丹. 储液罐动力学与控制研究进展[J]. 力学进展，2011，41(1)：79-91.

Yue Bao-zeng, Zhu Le-mei, Yu Dan. Recent advances in liquid-filied tank dynamics and control [J]. Advances in Mechanics, 2011, 41(1): 79-91.

[10] Mohammed B,Zu J W. Tractor-semitrailer model for vehicles carrying liquids [J]. Vehicle System Dynamics, 2006, 44(11): 871-885.

[11] 郑雪莲，李显生，任园园,等. 非满载罐体液体冲击等效机械模型参数确定[J]. 湖南大学学报:自然科学版，2013，40(6):53-58.

Zheng Xue-lian, Li Xian-sheng, Ren Yuan-yuan, et al. Parameter values of equivalent mechanical model for liquid sloshing in partially-filled tanks [J]. Journal of Human University (Natural Sciences), 2013, 40(6):53-58.

[12] Chandrasekharan S, Guenther D A, Heydinger G J, et al. Development of a roll stability control model for a tractor vehicle [J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2009, 2(1): 670-679.

[13] 胡晓明，李万莉，赵志国,等. 液罐车罐体内液体横向晃动研究[J]. 应用力学学报，2013，30(5)：641-646.

Hu Xiao-ming, Li Wan-li, Zhao Zhi-guo, et al. Horizontal fluid sloshing analysis in the body of tank truck [J]. Chinese Journal of Applied Mechanics, 2013, 30(5): 641-646.

[14] Lu Jian-bo, Messih David. An enhancement to an electronic stability control system to include a rollover control function [C]∥ SAE Paper, 2007-01-0809.

[15] 郑雪莲，李显生，任园园,等. 瞬时液体冲击对汽车罐车侧倾稳定性的影响[J]. 吉林大学学报:工学版，2014，44(3)：625-630.

Zheng Xue-lian, Li-Xian-sheng, Ren Yuan-yuan, et al. Rollover stability analysis of tank vehicle impacted by transient liquid sloshing [J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(3): 625-630.