汽车干式离合器滑磨噪声的影响规律分析*
龚雨兵 张德峰 周杰 葛文成
(桂林电子科技大学,桂林 541004)
1 前言
干式离合器总成具有传递效率高、压盘压紧力稳定、操纵力小等优点,在汽车上得到广泛应用[1]。当离合器总成接合时,在膜片弹簧压紧力作用下,离合器总成通过从动盘摩擦片上的摩擦扭矩带动从动盘总成和变速器输入轴一起转动以传递发动机动力。在实际使用中,某些离合器总成在接合过程中会产生滑磨噪声,该噪声的出现,严重影响乘车舒适性,增加维修成本。该噪声属于摩擦引起的振动和噪声,国内外学者利用解析法、数值分析法及试验法等研究方法对摩擦引起的振动噪声进行了大量研究。一般认为,摩擦面形貌[2-3]、摩擦面实际接触倾角[4-6]、摩擦因数[7-11]、摩擦面凸起[12]及压紧力[13]等对摩擦噪声的产生有重要影响。但现有研究主要是针对制动器中的制动尖叫,关于离合器总成中滑磨噪声的研究很少。本文以离合器总成的滑磨噪声为研究对象,以是否发生滑磨噪声为指标,通过复特征值分析方法,分析了摩擦因数、压紧力、摩擦片表面凸起、压盘温升及热变形等关键因素对离合器总成滑磨噪声产生的影响,并与实测数据进行对比分析。
2 滑磨噪声数值分析方法
2.1 复模态理论
近年来,基于复模态理论的复特征值分析方法已经成为摩擦噪声领域的主流分析方法[[88,,1144]]。在工业应用中,复特征值分析方法成为唯一的可用方法[[1155]]。汽车干式摩擦离合器总成动力学方程可以表示为:

式中,M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;F为压盘和飞轮与从动盘摩擦片之间的摩擦力矩阵;x为位移向量;ẋ为速度向量;ẍ为加速度向量。
式(1)中,质量矩阵、阻尼矩阵、刚度矩阵等都为对称矩阵。考虑摩擦力的作用,改写式(1)为:

式(1)中对称的刚度矩阵K变为式(2)中非对称矩阵Kf。式(2)在实空间里无法解耦,必须采用复模态分析方法。复模态分析方法有两种途径,分别是状态空间法和拉氏变换法。拉氏变换法在复域(或S域)中进行求解。在复域中,式(2)特征值可表示为:

式中,σ为特征值实部;ω为特征值虚部。
如果复模态的特征值具有非正实部,则该阶模态稳定。反之,如果复模态的特征值具有正实部,则该阶模态不稳定[[77--1111]],从而可能激发噪声,相应的虚部即为发生振动噪声的频率。因此,复特征值方法可以判断噪声发生趋势和特有噪声频率。
2.2 分析流程与方法
针对离合器总成的复特征值分析方法,首先对离合器总成有限元模型进行非线性静力学分析,仿真离合器总成工作时的真实接触状态,忽略阻尼矩阵C并将压盘与从动盘摩擦片之间的摩擦力作为外力引入到振动微分方程(1),使原本对称的刚度矩阵K变成非对称矩阵。其次,利用线性摄动法,对引入摩擦后具有非对称刚度矩阵的有限元模型进行复模态分析,根据得到的复特征值实部的正负来判断系统是否稳定。由于在分析中忽略了材料阻尼的影响,分析结果存在过预测,现有研究认为阻尼比ζ≤-0.01的不稳定模态才能发出滑磨噪声[[77]]。由于各阶不稳定模态的阻尼比ζ符号总是与实部符号相反,其数值大小近似等于实部与虚部的比值,为便于观察,将的不稳定模态转换成进行表示。
2.3 有限元模型
以某公司Φ260离合器总成为原型建立有限元模型,重要部件材料参数如表1所示。为便于计算,对从动盘内花键部分进行简化(花键齿部未进行建模)。有限元整体模型中,单元总数为270 568,节点总数为850 144。其中,压盘零件有限元模型如图1a所示,从动盘总成有限元模型如图1b所示。

表1 材料参数
根据离合器总成实际工作和约束情况,在压盘齿顶施加压紧力载荷;在压盘孔位置施加位移约束,限制径向位移;在从动盘内花键处施加位移约束,限制径向位移和切向转动;在从动盘摩擦片与飞轮接触的外表面施加零位移约束(模拟飞轮);在压盘与从动盘摩擦片之间建立摩擦接触对,并生成内部滑移运动,指定摩擦因数与转速。
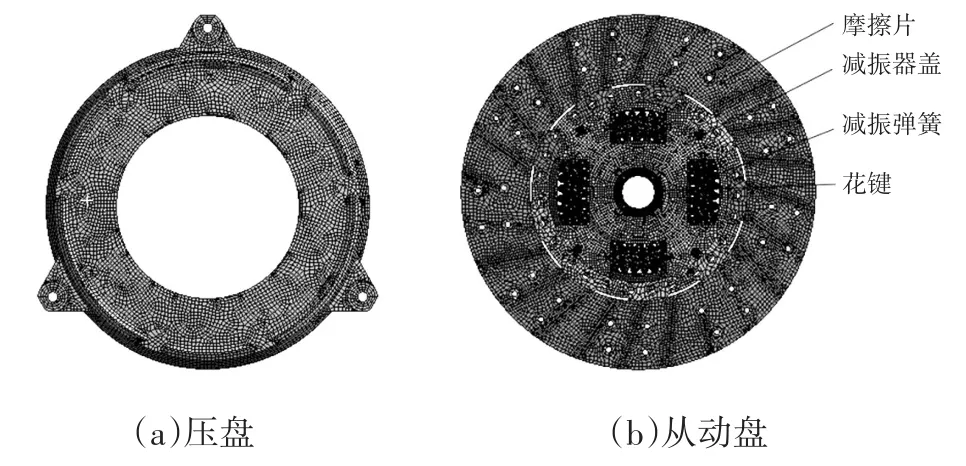
图1 离合器有限元模型
3 结果分析
3.1 摩擦因数
在压盘齿顶压紧力为5 kN时,不同摩擦因数下的离合器总成不稳定模态的实部(稳定系数)和虚部(频率)如图2a所示。由图2a可以看出,摩擦因数是影响滑磨噪声产生的重要因素,随着摩擦因数的增加,离合器总成不稳定模态的数目也在增加。阻尼比的不稳定模态个数在摩擦因数为0.1、0.2、0.4、0.6时分别为0个、1个、2个、2个,并且实部随着摩擦因数的增加而增大。这说明随着摩擦因数的增大,会增大滑磨噪声发生的趋势。以19阶和20阶模态为例,随着摩擦因数的增加,19阶频率逐渐上升,20阶频率逐渐下降,两者最终重合,发生模态耦合,如图2b所示。这一影响规律与制动器中摩擦因数对制动尖叫的影响规律相似,反映出离合器总成的滑磨噪声与制动器的制动尖叫在本质上有一定相似性。
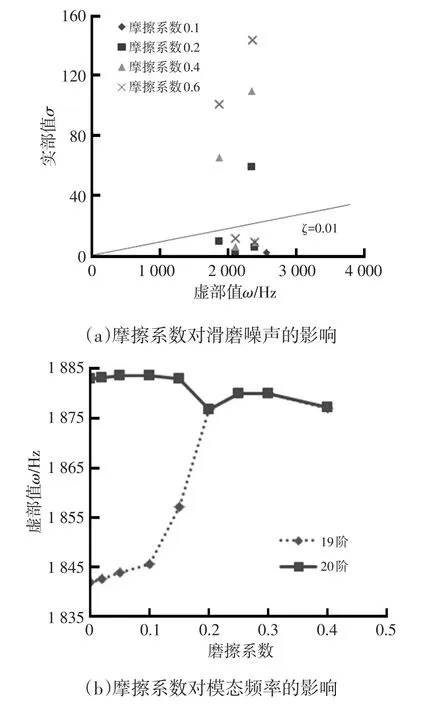
图2 摩擦系数的影响
3.2 压紧力
压盘与从动盘摩擦片之间的压紧力是离合器总成的重要设计指标。摩擦因数为0.4时,不同压紧力载荷下的离合器总成不稳定模态的实部和虚部如图3所示。由图3可以看出,压紧力由1 kN增大到3 kN时,不稳定模态的实部增加、虚部变化较小,|ζ|≥0.01的不稳定模态个数由2个增加为3个。压紧力由3 kN增大到6 kN时,不稳定模态的实部增加、虚部变化较小,|ζ|≥0.01的不稳定模态个数由3个减小为2个。即压紧力上升时,会增大滑磨噪声发生的概率,但当压紧力超过一定数值后,滑磨噪声发生概率会降低。压紧力与摩擦生热特性、温度场、位移场等相关,因此其影响规律表现形式较为复杂。

图3 压紧力对滑磨噪声的影响
3.3 摩擦片表面凸起
由于加工工艺的影响,实际从动盘摩擦片表面并不是理想的平面,其初始端面跳动(SRO)是不可消除的几何特征[[1166--1177]]。建立图4所示的从动盘摩擦片表面凸起模型来模拟实际存在的端面跳动,在圆周方向上,从动盘摩擦片的厚度符合正弦分布。在压盘齿顶施加5 kN压紧力载荷、摩擦因数为0.4时,从动盘摩擦片表面在不同正弦凸起高度下的不稳定模态实部和虚部如图5所示。由图5可知,凸起高度增加会使滑磨噪声的频率降低,减小复模态实部但不会减少不稳定模态的个数;在理想平面下,离合器总成的滑磨噪声更趋于高频;在凸起存在的情况下,离合器总成的滑磨噪声更趋于低频。从动盘摩擦片表面凸起,改变了接触面上的接触压力分布,继而改变温度场、热变形场分布,因而改变滑磨噪声特性,其具体影响规律也会较为复杂。

图4 摩擦片凸起示意图

图5 端面跳动对滑磨噪声的影响
3.4 压盘温升及热变形
离合器总成在接合过程中,压盘与从动盘摩擦片相对滑动摩擦,引起摩擦面温度上升与压盘热变形,致使实际接触面积可能远小于名义接触面积,从而改变压盘与从动盘摩擦片的热接触特性。数值分析中,在接合阶段,对压盘摩擦面施加随时间变化的热流密度,模拟压盘与从动盘摩擦片之间因滑动摩擦而产生的热量[18]。根据离合器总成工作工况,压盘与从动盘摩擦片接合时间和分离时间分别为2.5 s和1 s,接合次数为5次、环境温度为22℃。
图6为压盘在工作时的温度场。图7a、图7b为压盘热变形前、后压盘与从动盘摩擦片的实际接触状态,分别有远离接触(far)、接近接触(near)、接触滑移(slid⁃ing)和粘连(sticking)等不同接触状态。由图6可以看出,在滑动摩擦后压盘温度明显上升,且外圈温度明显高于内圈。由图7a、图7b可以看出,随着压盘温度的上升,压盘与从动盘摩擦片实际接触区域由整个压盘面变为仅在压盘内圈接触,压盘变形表现为“内凸”,与实际情况相吻合。图8为压盘变形前、后对应的不稳定模态实部和虚部。由图8可以看出,考虑压盘热变形后离合器总成不稳定模态的实部与虚部都下降,且不稳定模态个数也降低。其中,实部最大值由变形前的110降低到变形后的18,对应虚部由变形前的2 357 Hz降低到变形后的 1 288 Hz,|ζ|≥0.01的不稳定模态个数由压盘变形前的2个减小为变形后的1个。说明摩擦引起的压盘“内凸”变形会降低离合器总成滑磨噪声频率与强度,并减少滑磨噪声发生趋势。压盘温升及热变形显著改变了压盘与从动盘摩擦片的接触面积,继而对摩擦热接触特性产生显著影响,继而影响滑磨噪声。
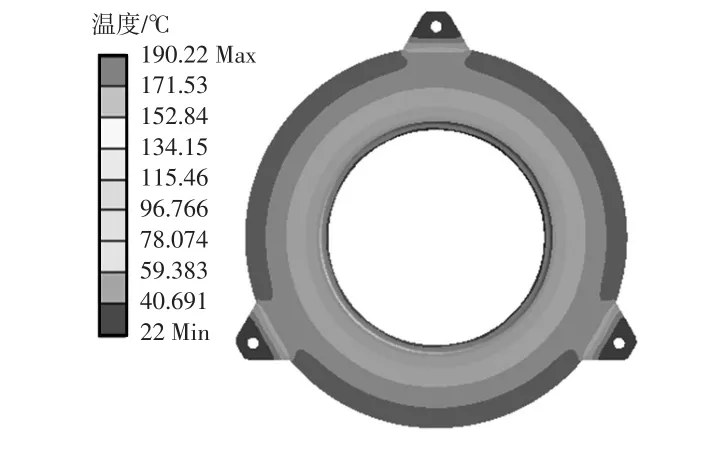
图6 压盘温度场

图7 压盘变形前、后接触状态

图8 压盘变形前、后对滑磨噪声的影响
4 实车试验与对比
4.1 试验
在某汽车维修服务站对存在滑磨噪声的车辆进行实车噪声数据采集,采用Φ260离合器总成。试车方法如下:
a.在水泥路面试车。挂1挡起步加油(转速1 000 r/min左右),在行驶过程中换到其它高挡位(1 500-2 000 r/min)并加大油门加速行驶。
b.在泥泞路面试车(包括上坡)。挂1挡起步加油(转速1 000 r/min左右),在行驶过程中换到其它高挡位(1 500-2 000 r/min)并加大油门加速行驶。
测试结果发现,故障车辆在半离合加速时出现滑磨噪声,滑磨噪声的产生存在明显间歇性,与摩擦噪声发生特性相符[14]。对噪声进行频率采样,得到3个主要的噪声频率,分别为494 Hz、634 Hz、1172 Hz(噪声强度≥100 dB)如图9所示。
故障车辆在第一次爬坡时(坡度约30°),半离合加速出现滑磨噪声,但第二次和第三次爬坡都不再出现滑磨噪声。对故障车离合器总成进行返厂测试,各项性能参数均符合技术要求,从动盘摩擦片的端面全跳动为0.6 mm(<1 mm为合格)。
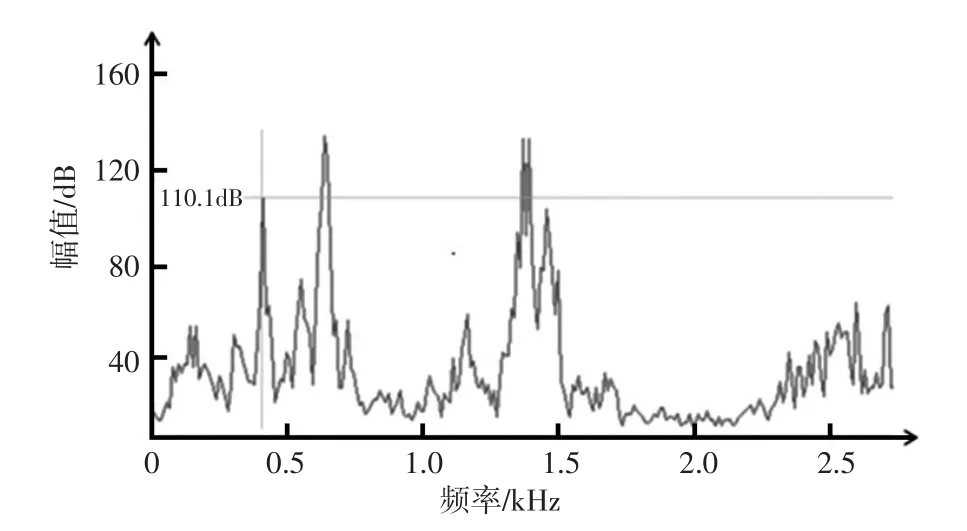
图9 滑磨噪声频谱图
4.2 对比
在压盘齿顶压紧力为5 000 N、摩擦因数为0.4,从动盘摩擦片表面存在正弦凸起,凸起高度为0.3 mm(全跳动0.6 mm)的情况下,采用复特征值分析法预测到2阶不稳定频率分别为1 072 Hz、1 391 Hz(见图5)。对比试验结果的494 Hz、634 Hz、1 172 Hz,复特征值分析法比较准确的预测到了噪声发生强度较大的1 172 Hz(由于误差的存在,预测频率偏移为1 072 Hz),但同时漏掉了494 Hz、634 Hz,存在漏阶现象[10,11,14]。试验中车辆在多次爬坡(持续滑磨)引起压盘温度上升后滑磨噪声消失,该情况与复特征值法中压盘温度及热变形对离合器总成滑磨噪声的影响趋势(见图8)基本相符。
5 结束语
针对离合器总成的滑磨噪声,采用复特征值分析方法分析了多种因素对滑磨噪声的影响规律并与试验数据进行对比。各影响因素在所选定的数值范围内,表现为:
a.较小的摩擦因数可以明显减少滑磨噪声。摩擦因数由0.1增加到0.4时,噪声频率由0个增大到2个。
b.压紧力的初始增加会加剧滑磨噪声,之后随着压紧力的增加滑磨噪声会减小。压紧力由1 kN增大到3 kN(|ζ|≥0.01)时的不稳定模态个数由2个增加为3个。压紧力由3 kN增大到6 kN(|ζ|≥0.01)时的不稳定模态个数由3个减小为2个。
c.由摩擦片表面正弦凸起引起的滑磨噪声多发生在低频(<2 000 Hz)。
d.压盘温度升高及其内凸变形可以减少滑磨噪声发生趋势。不稳定模态实部最大值由变形前的110降低到变形后的18,对应虚部由变形前的2 357 Hz降低到变形后的1 288 Hz,|ζ|≥0.01的不稳定模态个数由变形前的2个减小为变形后的1个。
[1]林世裕.膜片弹簧与碟形弹簧离合器的设计与制造[M].南京:东南大学出版社,1995:18-20.
[2]王东伟,莫继良,王正国,王晓翠,陈光雄,朱旻昊.沟槽织构化表面影响摩擦振动噪声机理[J].机械工程学报,2013,23:112-116.
[3]Wang X C,Mo J L,Ouyang H J,et al.Squeal Noise of Friction Material with Groove-Textured Surface:an Experimental and Numerical Analysis[J].Journal of Tribology,2016,138(2):21401.
[4]Vayssière C,Baillet L,Linck V,et al.Influence of Contact Geometry and Third Body on Squeal Initiation:Experimentaland NumericalStudies:World Tribology CongressIII,2005[C].
[5]Lv H,Zhang L,Yua Z.Influence of Surface Run-out on Disc Brake Squeal[J].Journal of Vibroengineering,2013,15(2):520-531.
[6]吕红明,张立军,余卓平.接触表面不平度对摩擦尖叫噪声的影响[J].摩擦学学报,2011,31(5):473-479.
[7]侯俊,过学迅.基于有限元方法的盘式制动器制动噪声研究[J].机械设计,2008,08:50-52.
[8]陈光雄,戴焕云,曾京,周仲荣.踏面制动尖叫噪声的有限元分析[J].机械工程学报,2009,03:203-207.
[9]张光荣,谢敏松,黎军,齐钢,浦新宇.摩擦片偏磨引起的汽车制动低鸣噪声[J].机械工程学报,2013,09:81-86.
[10]陈康.盘式制动啸叫的实验研究与仿真分析[D].哈尔滨工业大学,2014.
[11]韦健,孙跃东,王书文,周萍.基于ABAQUS的盘式制动尖叫分析[J].机械设计与制造,2016,06:151-154.
[12]Bonnay K,Magnier V,Brunel J F,et al.Influence of Geometry Imperfectionson SquealNoise Linked to Mode Lock-in[J].InternationalJournalofSolids and Structures,2015,75-76:99-108.
[13]Hetzler H,Willner K.On the Influence of Contact Tribology on Brake Squeal[J].Tribology International,2012,46(1):237-246.
[14]张立军,刁坤,孟德建,庞明.摩擦引起的振动和噪声的研究现状与展望[J].同济大学学报(自然科学版),2013,05:765-772.
[15]CantoniC,CesariniR,Mastinu G,etal.Brake Comfort-a Review.Vehicle System Dynamics,2009,47(8):901-947.
[16]孟德建,张立军,余卓平.初始端面跳动对制动器热-机耦合特性的影响[J].同济大学学报(自然科学版),2012,02:272-280.
[17]方向东.离合器从动盘总成端面跳动校正工艺的研究[J].湖北农机化,2015,06:60-61.
[18]邢预恩等,换档离合器摩擦片温升分析[J].现代制造技术与装备,2007(05):17-19.

