汽车视野二维角度坐标法的二次开发及应用

姚树寅 王洋 冯斌 张健 冉云飞

（1.中国重型汽车集团技术发展中心，济南 250102；2.重庆长安汽车工程研究总院，重庆 401120；3.西安双特智能传动有限公司，西安 710119；4.弗吉亚（重庆）汽车部件系统有限公司，重庆 401122）

1 前言

视野分析和校核是汽车研发过程中的重要工作。随着三维设计软件的广泛应用，通过3D数据可以立体直观地进行驾驶员视野的相关分析，这也是目前普遍采用的方法。这种方式立体、形象、准确度高，但作图过程较为复杂，由于大量3D数据的存在，生成的线条在一定程度上干扰视觉，表达略显凌乱。而理论上，如果不考虑光线眩目或亮度不足等外部影响，在视线可及距离内，目标物是否方便可见通常只与其所处的视线角度及其所占据的视角大小有关。McIsaac,E.J.等在1995年就提出了一种二维角度坐标图[1]的表达方法。

二维角度坐标图能够包含大量的视野信息，只需2个角度参数即可表达目标点，与3D数据分析相比，在表达上更加简洁直观。但到目前，其研究和应用较少，原因包括：生成二维角度坐标图需进行大量数据换算，如无合适的方法，将非常繁琐耗时；利用3D数据可直接实现各种视野分析，视野分析通常只针对某一局部开展，也就不需要生成完整的二维角度坐标图。本文尝试开发了二维角度坐标图的快速生成程序，并对其应用可行性进行了探讨。

2 二维角度坐标法

McIsaac,E.J.等提出，人的视野可理解为如图1所示模型[2]。人处在以人眼为中心的球体内部，目标点分布在球面上，人通过眼睛及头部的转动找到目标点。这样，以眼点（球心）为参考，连接每个目标点的视线都可以通过水平方位角和纵向举升角来表示，从而将三维直角点坐标转换为二维角度坐标，简化问题。

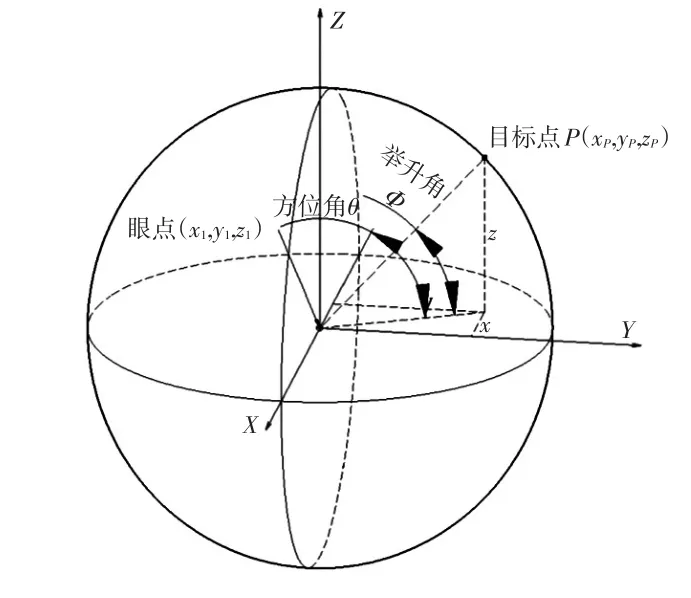
图1 二维角度坐标法视野模型

需要注意的是，该模型是建立在视野分析校核只与角度有关的基础上的，因为方位角和举升角只能确定视线的方向，并不能完全确定目标点位置。这是与实际情况相符的：对于方位角和举升角相同，与眼点距离不同的目标点，人只能观察到近处的目标点，而较远的目标点则会被遮挡。

同样，在进行人机布置和视野分析时，特别是直接视野分析时，通常只需分析目标物是否在舒适视角区域内、是否被遮挡等，只需确定视线方向即可进行，因此，通过方位角和举升角可以实现对视野的分析。

二维角度坐标图中包含着大量的视野信息，但其生成过程需要大量的数据计算。因此，开发二维角度坐标图的自动生成程序，对视野分析非常有利，对于二维角度坐标法的应用和推广也具有积极意义。

3 二维角度坐标图自动生成程序开发分析

3.1 输入条件

程序的核心功能是实现点的坐标变换。方程未知的曲线无法进行坐标变换，因此需将待变换的曲线进行点化处理：在曲线上提取足够的点，利用这些点进行坐标变换。

同时，完成坐标变换需要参考点，视野分析的参考点一般是眼点。因此，输入条件需要包含眼点及待转换的目标点或曲线。

3.2 变换规则

为保持与乘用车规定坐标系[3]和驾驶员习惯一致，规定从眼点沿车辆X轴负方向作射线，其方位角、举升角均为零，其右侧目标的方位角为正，左侧目标的方位角为负，其上方目标的举升角为正，下方目标的举升角为负。

在三维直角坐标系中，设眼点E1的坐标为(x1,y1,z1)，目标点P的坐标为(xP,yP,zP)。令x=xP-x1、y=yP-y1、z=zP-z1，则P相对于E1的坐标为(x,y,z)。则方位角θ、举升角Φ分别为：

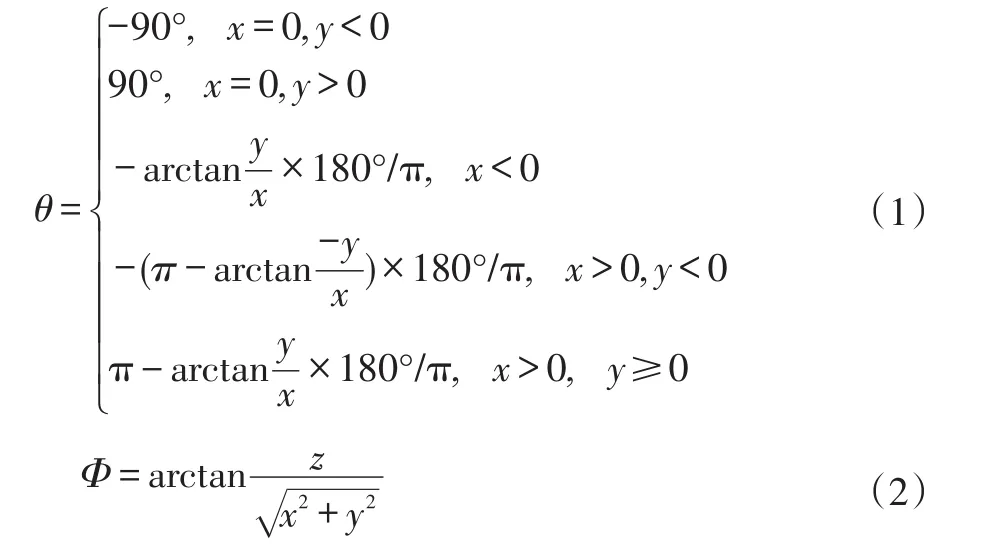
3.3 输出结果

坐标转换的直接结果为二维坐标点，将这些点连接成曲线，就完成了对输入曲线的变换。

4 程序代码

根据上述分析结果，本文采用CATIA V5R21作为设计工具，以VB6.0作为开发工具完成程序开发。

下面对程序部分核心代码进行说明，本文省去了部分对象的定义语句，保留了功能代码。

4.1 调用CATIA程序

首先调用CATIA程序，并将CATIA当前活动文档的part文件定义为工作对象[4]。

4.2 提取输入条件

采取的输入方式是选择输入，这种方法便于控制输入对象。

4.3 将选择的对象加入列表

将上节中选择的对象加入List1，以便循环引用。

4.4 将选中的线点化

将List1中的线点化，每条线上提取大量点以便将输入的线进行坐标变换。

4.5 坐标变换

根据前文对目标点和眼点等的坐标设定及推导的变换规则，将上面提取的点进行坐标变换。

4.6 新建点

按变换后的坐标值新建点。

4.7 连结曲线

将坐标变换后的点连结成曲线，就得到了曲线的二维角度坐标图。

4.8 更改曲线属性

为便于区分最终结果，可以将曲线的部分属性进行调整。

4.9 生成程序

在VB程序界面，引用CATIA资源库，将代码进行打包生成程序，得到的程序界面如图2所示。

图2 程序界面

5 程序运行及结果讨论

5.1 程序运行步骤

a.运行CATIA软件，打开存储待转换曲线的文件。本文以输入图3所示的各边界曲线为例。

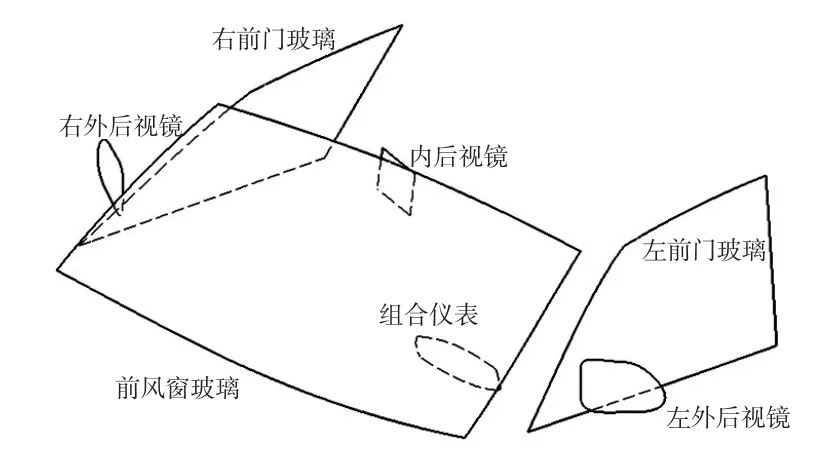
图3 待转换的特征曲线示意

b.运行二维角度坐标转换程序，并将相关参数输入程序界面。需指出的是：每条输入线上点的数目会影响最终得到的曲线，点的数目越多，转换得到的曲线越精确。

c.在CATIA程序界面选择需转换的曲线，程序自动开始运算。

d.程序自动完成运算，生成的二维角度坐标图结果见图4。

图4 转换结果

5.2 结果验证

为检验这种方法的准确性，从3D图中任取一点进行对比验证，验证结果如图5所示。由图5可知，3D图和二维角度坐标图中对应点的方位角和举升角测量结果相同，表明这种转换方式是正确的。

5.3 结果分析

从转换得到的二维角度坐标图（图4）中，还可以得到以下结论：

a.二维角度坐标图能够直观地区分单眼视野、双眼视野以及双单眼视野[5]。对分析单眼盲区、双眼盲区（如A柱障碍角、组合仪表可视性）等非常方便。

图6所示为按照SAE1050中规定的方法和利用二维角度坐标图获得的左A柱障碍角的分析结果，两种方法分析结论一致，但后者的表达更加直观，并能分别测得该位置左、右眼点的左A柱单目障碍角。

b.二维角度坐标图直接地表达出各特征所占据的视角大小，并评价其可视性。

图5 曲线上任意点的方位角和举升角结果对比

图6 左A柱障碍角的分析结果对比

在图4中，可以直接估读出组合仪表在左眼视野中所占据的视野角度范围：方位角约-15°~20°，举升角约-25°~-15°。

图7所示为以3D数据方法和利用二维角度坐标图测得的组合仪表可视性分析结果。其中，θL为左侧方位角；θR为右侧方位角；ФT为上方举升角；ФD为下方举升角。估读得到的结果与两种方法分析得到的结果一致，但在二维角度坐标图中可以直接测量得到，过程大大简化。

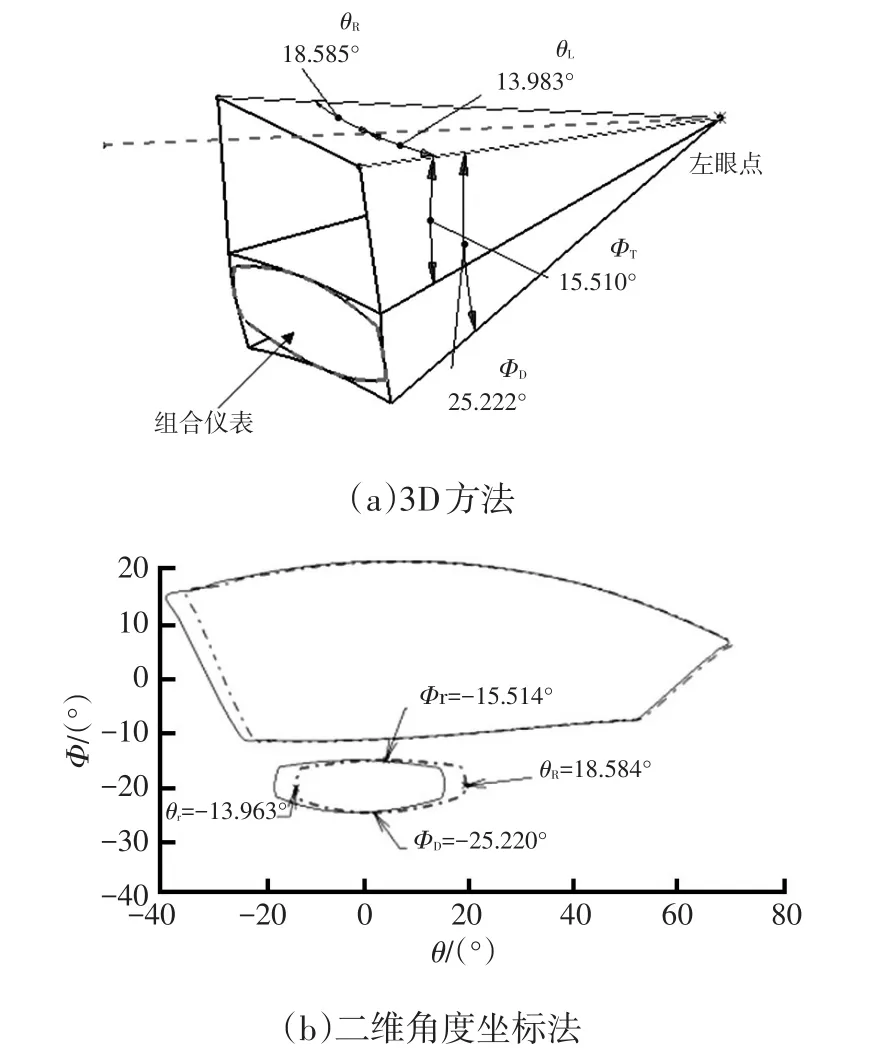
图7 左眼点组合仪表视野分析结果对比

c.二维角度坐标图反映了距离对视角大小的影响。如对称布置的左、右前门玻璃，由于与眼点的距离不同，在视野中所占据的视角范围也不相同。

5.4 二维角度坐标图的其他作用

二维角度坐标图能够帮助理解不同因素对视野的影响。不同人体及其位置的眼点视野角度如图8所示，它清晰地反映了人体位置和高度对视野的影响：对于同一人体，座椅前端位置前方视野更好，但组合仪表等内部视野舒适性不如座椅后端；对于同一位置的不同人体，高百分位人体的下视野优于低百分位人体，上视野和组合仪表等内部视野较低百分位人体差。二维角度坐标图反映的这些信息，对于理解和辅助视野设计有很好的指导作用。

图8 不同人体及其位置的眼点视野角度

6 结束语

二维角度坐标图包含大量的视野信息，为汽车视野分析提供了除3D数据方法外的另一种选择，且分析更为简便，在表达上更为直观。二维角度坐标图的自动计算和生成，省去了繁琐的操作过程，便于二维角度坐标图的应用。

[1]McIsaac EJ,BhiseVD.Automotive Field of View Analy⁃sis Using Polar Plots[C]//International Congress&Ex⁃position.1995.

[2]Bhise V D.汽车设计中的人机工程学[M].北京：机械工业出版社，2014.

[3]中国国家标准化管理委员.汽车驾驶员前方视野要求及测量方法：GB 11562—2014[S].2014.

[4[胡挺，吴立军.CATIA二次开发技术基础[M].北京：电子工业出版社，2006.

[5]Society of Automotive Engineers.Describing and Mea⁃suring the Driver's Field of View:J1050[S].2003.