基于BP-EKF算法的电池SOC估计*
徐艳民
(1.广东机电职业技术学院,广州,510515;2.华南理工大学,广州,510641)
1 前言
电动汽车电池的荷电量SOC无法直接测量,只能通过电池的外部特征进行估计。但是电动汽车的电池端电压在使用过程中变化很大,使得电池在工作过程中具有高度的非线性,增加了电池SOC估计的难度。当前电池SOC的估计方法分为两类,一是通过研究电池内部的化学反应和工作原理来估计电池SOC,但是此类方法成本高、研究复杂、通用性差;二是通过建立电池模型,测量电池的电压、电流等参数来估计电池SOC,此方法成本较低,且通用性好。国内外对电池SOC的估计问题研究较多,文献[1,2]使用自适应卡尔曼滤波算法,对电池健康程度进行加权,可以准确估计出未知老化程度的电池SOC;文献[3,4]使用无迹卡尔曼滤波算法,更加准确地逼近了电池的非线性系统,提高了电池SOC估计精度;文献[5,6]使用QPSOBP神经网络方法对电池SOC进行估计,通过对神经网络进行训练实现对电池SOC的准确估计。
对电池SOC的估计要求精度高、速度快、初始误差大时也能快速回归等。为了满足这些要求,本文设计了BP-EKF算法,此算法不仅具有很高的收敛精度,而且反应快,可以快速收敛至理论值附近,能够满足当前电动汽车的使用要求。
2 电池状态空间方程
2.1 电池等效模型
电池的等效模型是将电子器件连成电路,模拟电池内部状态,其目的是通过测量电流、电压、温度等外部特征间接计算内阻、SOC等内部参数。电池的常用模型[7]有理想模型、线性模型、Thevenin模型等。理想模型是将电池等效为一个电动势,忽略其它因素,对电动车而言此模型与现实情况差距太大,无法使用;线性模型将电池等效为一个电动势和内阻串联,此模型过于简单,省略了电池的动态过程。
本文使用的电池模型为Thevenin模型,模型等效电路如图1所示。图中,UOC为等效电池的开路电压,R0等效为电池的欧姆内阻,RP等效为电池的极化电阻,CP等效为电池的极化电容,RPCP构成的RC网络可以模拟电池极化过程的动态过程。

图1 Thevenin模型
2.2 模型参数测试与状态空间方程
本文所使用电池为5 Ah的磷酸铁锂电池。将电池在满电情况下,以0.5 A电流脉冲放电25 min,然后静置,记录整个过程中电池端电压,结果如图2所示。

图2 放电过程的端电压
图2中,V1表示断电瞬间由于内阻分压消失引起的端电压变化,V2表示极化过程中电压的变化,3τ为电压升至95%平稳电压的时间。从图中可以看出,Thevenin模型中内阻R0可以模拟V1的变化过程,RPCP构成的RC网络可以模拟V2的变化过程,即Thevenin模型完全可以将电池放电过程中的主要变化模拟出来,所以本文对电池SOC估计时使用Thevenin模型。
使用连续脉冲恒流放电的方法对模型参数进行测试,首先将5 Ah的电池充满静置24 h,然后以1 A的恒流放电0.45 h,静置0.5 h后再次以1 A的恒流放电0.45 h,如此循环直至放电至截止电压,每次放电量约为10%。试验结果如表1所示。
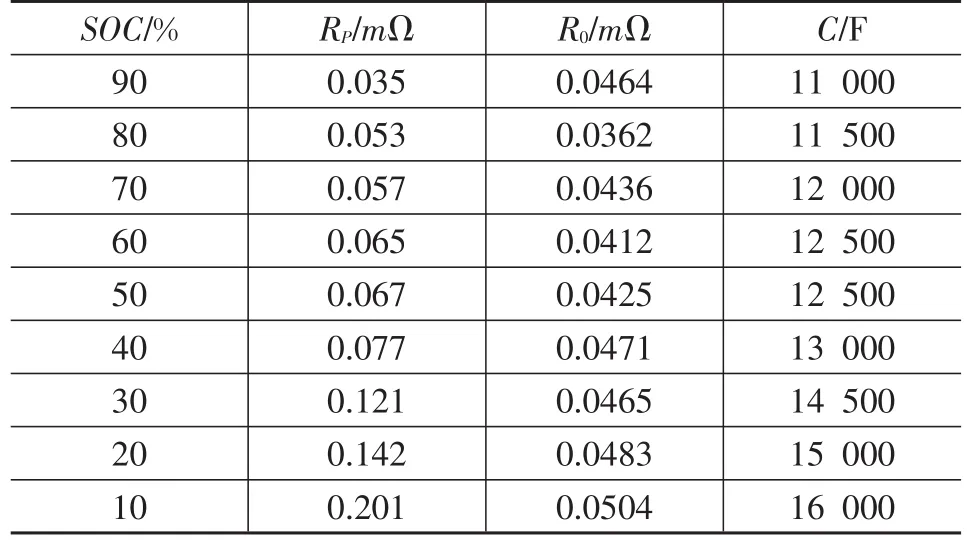
表1 Thevenin模型参数值
将实际使用的电池进行放电试验,与此Thevenin模型进行比较可以看出,Thevenin模型可以准确模拟出电池放电过程,相对误差最大为2%。
选择电池SOC、极化电容两端电压Up为状态量端电压U1为输出量,电流i为输入量,则可建立状态空间方程为:
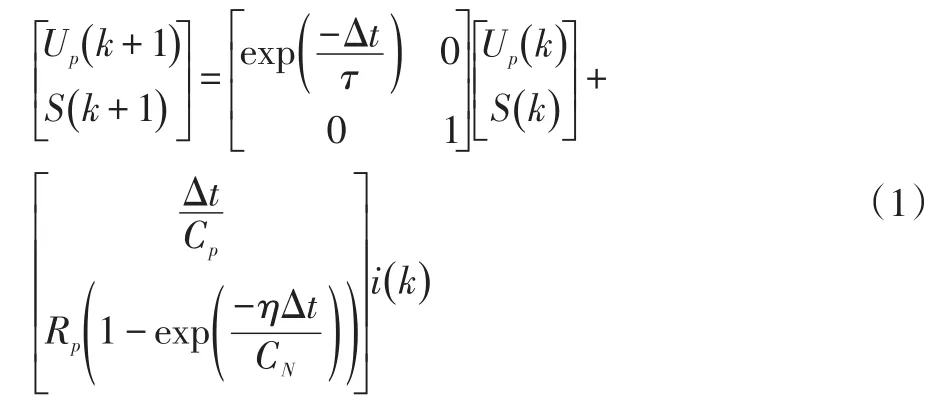
式中,Δt为采样间隔;τ为积分时间常数且有τ=RpCp;η为库伦效率;CN为当前状态下的电池最大容量。
输出方程为:

为了确定开路电压UOC与SOC的对应关系,本文设计了恒流间歇放电试验。以0.5 A的恒流对磷酸铁锂电池放出一定量的电量,然后静置1 h,测其开路电压。为了提高拟合精度,本文选择对UOC-SOC曲线进行分段拟合,拟合曲线为:

测试值与拟合曲线如图3所示,从图3中可以看出,拟合曲线与实测值拟合程度很高。

图3 UOC-SOC拟合曲线
3 BP-EKF算法
3.1 扩展卡尔曼滤波算法
扩展卡尔曼滤波[8](Extended Kalman Filter,EKF)将卡尔曼滤波的应用范围扩展到非线性系统,此算法将非线性系统近似线性化,从而满足卡尔曼滤波使用的条件。非线性系统空间方程为:

式中,W(k)为状态噪声;V(k)为观测噪声。
使用泰勒级数展开方法,只保留一次项,将此非线性系统线性化,得:
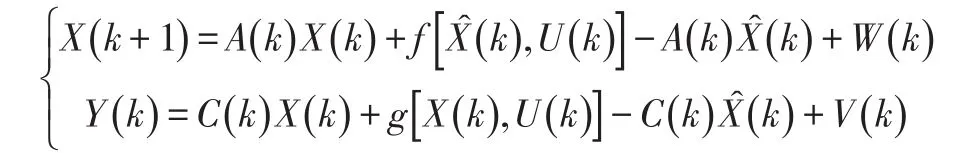
使用上述方法对式(1)和式(2)给出的空间方程进行线性化,得:

将电池等效模型进行线性化后就可以使用卡尔曼基本公式进行滤波,滤波的迭代公式为:

式中,Q(k)为状态噪声方差阵;R(k)为观测噪声方差阵。
3.2 BP-EKF算法介绍
EKF算法将非线性系统近似为线性系统的过程中,省略了泰勒展开的高阶项,对于高度非线性系统,会产生巨大的非线性误差。而磷酸铁锂电池在使用过程中表现出非常复杂的非线性,因此单独使用EKF算法估计电池SOC会产生较大误差,所以本文提出了BP-EKF算法,使用BP神经网络算法对EKF进行补偿和优化,进一步提高了SOC估计精度。
3.2.1 BP神经网络算法
BP神经网络[9](BackPropagation Neural Network)是误差反向传播的前向神经网络,是当前应用最为广泛的一种神经网络结构。BP神经网络结构分为输入层、隐含层和输出层,其中隐含层可以为一层也可以为多层,最简单的BP神经网络结构为三层结构,此结构可以无限逼近任意连续函数,其结构图如图4所示。
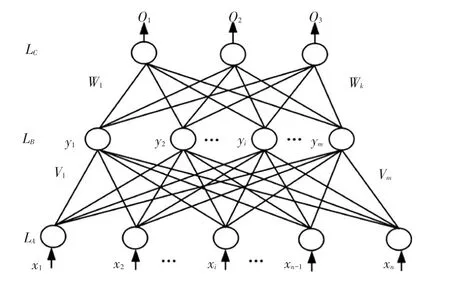
图4 BP神经网络结构
图4中,LA、LB、LC分别表示输入层、隐含层和输出层。表示输入层LA的输入向量,表示隐含层的输出,{}0i表示输出层的输出向量,vij表示LA层的第i个神经元到LB层的第j个神经元的传递权值,wij表示LB层的第i个神经元到LC层的第j个神经元的传递权值。
BP神经网络的工作原理是,输入经输入层进入神经网络,经隐含层和输出层处理后输出,若输出值与期望输出误差较大,则误差反向传播,通过调整神经元之间的传递权值,使得神经网络输出与期望输出在误差范围内。
为了实现对EKF算法的优化,考虑电池等效模型,本文选用输入层神经元数为4、隐含层为10、输出层为1的三层网络结构。输入量分别为,输出量为
3.2.2 BP-EKF算法设计
BP神经网络对EKF算法的优化,不仅弥补了EKF的非线性误差,而且降低了对电池模型的精度要求,同时提高了SOC估计精度。其算法过程为:
a.BP神经网络的训练过程。对5Ah的磷酸铁锂电池进行不同放电电流下的放电试验,然后使用建立的电池模型和EKF算法处理数据,得到训练神经网络使用的和通过训练确定神经元之间的传递权值。
b.算法的实时估计。首先给出算法的结构图如图5所示。此算法的实质是,使用训练完的BP神经网络计算出SOC实际值与估计值之间的误差,对EKF的状态估计值进行补偿,从而使计算得到的SOC更加精确。精确的SOC估计值会决定下一时刻的模型参数值,所以SOC值的精确估计影响全局。

图5 BP-EKF算法结构图
BP-EKF算法的优势表现在:对电池无特殊要求,因此具有普适性,容易推广;可以补偿EKF的非线性误差,提高SOC估计精度;神经网络的自学习能力和对函数的逼近能力,使得此算法对电池模型精度要求不高。
4 试验验证
4.1 试验设计
首先是BP神经网络的训练。本文使用的BP神经网络为三层结构,从输入层到输出层神经元的数量分别为4、10、1。设置训练的最大迭代次数为5 000,期望误差为10-4,使用 5Ah电池在不同放电电流下的采集数据共2 500组,试验迭代至1 795次时达到精度要求,训练完毕。在不同放电电流下进行放电试验重新采集500组数据,对训练结果进行验证,神经网络预测值与实际值相对误差在1.5%以内,说明神经网络可以以较高精度估计SOC误差值。
对BP-EKF算法进行验证。使用训练完的神经网络和EKF算法搭建BP-EKF算法,验证此算法在无初始估计误差、有初始估计误差、无初始估计误差但加入噪声、有初始估计误差且加入噪声4种情况下的SOC估计表现。根据电池实际情况,将电池初始电量真值设置为94%,初始估计误差设置为14%,加入的噪声为方差0.01的高斯白噪声。使用美国城市道路循环工况电流(Ur⁃ban Dynamometer Driving Schedule,UDDS)[10]模拟电动汽车使用过程中的电池电流,此电流模拟汽车的加速、减速、怠速和恒速过程,电流的一个周期为1 370 s。
4.2 数据处理及结论
将系统噪声初值设置为Q=[0.1,0.1;0.1,0.1],观测噪声R=1,状态误差协方差初值,仿真时间设置为6 000 s。分别使用BP-EKF算法和EKF算法对4种情况下的电池SOC进行估计,最终收敛误差如表2所示。
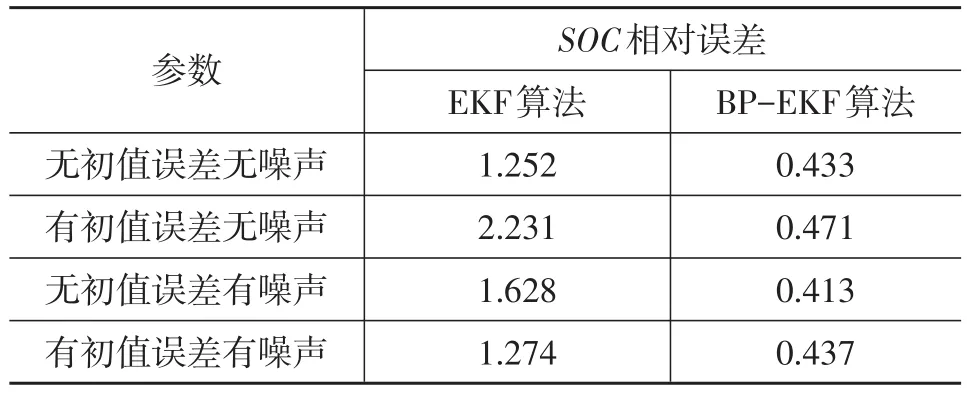
表2 BP-EKF与EKF估计误差对比 %
由于篇幅限制,本文只以图形方式给出了初始误差为14%且掺入噪声时的数据处理结果。结果如图6所示。

图6 有初值误差加噪处理结果
分析图6和表2中的数据,可以得到以下结论:
a.从图6可以看出,在初值误差为14%时,300 s后就接近理论值,说明BP-EKF算法收敛很快,可以满足使用要求。
b.在初值误差较大、加入噪声的情况下,BP-EKF算法收敛精度依然很高,说明BP-EKF算法具有很好的鲁棒性。
c.对比4种情况下两种算法的SOC估计精度可以看出,BP-EKF算法相对EKF算法,SOC估计精度提高70%左右,充分说明了此算法的有效性,此算法对SOC的估计速度和精度可以满足电动汽车使用要求。
5 结束语
本文介绍了当前常用的几种电池等效模型,通过试验选取了适用于磷酸铁锂电池的等效模型并进行了参数辨识,建立了电池的状态空间方程;分析了扩展卡尔曼滤波算法和BP神经网络算法,提出了BP-EKF算法,使用此算法对4种情况下的电池SOC进行估计,与EKF算法进行对比可以看出,本文提出的算法反应速度快、收敛精度高、鲁棒性好。
[1]魏克新,陈峭岩.基于多模型自适应卡尔曼滤波器的电动汽车电池荷电状态估计[J].中国电机工程学报,2012,32(31):19-26.
[2]Charkhgard M,Farrokhi M.State-of-Charge Estimation for Lithium-Ion Batteries Using Neural Networks and EKF[J].IEEE Transactions on IndustrialElectronics,2011,57(12):4178-4187.
[3]魏克新,陈峭岩.基于自适应无迹卡尔曼滤波算法的锂离子动力电池状态估计[J].中国电机工程学报,2014(3):445-452.
[4]么居标,吕江毅,任小龙.基于无迹卡尔曼滤波的动力电池荷电状态估计[J].电源技术,2014,38(9):1629-1630.
[5]Sun B X,Wang L.TheSOCEstimation of NIMH Battery Pack for HEV Based on BP Neural Network[C].IntelligentSystemsand Applications,2009.ISA 2009.International Workshop on.IEEE,2009:1-4.
[6]刘征宇,杨俊斌,张庆,等.基于QPSO-BP神经网络的锂电池SOC预测[J].电子测量与仪器学报,2013,27(3):224-228.
[7]林成涛,仇斌,陈全世.电流输入电动汽车电池等效电路模型的比较[J].机械工程学报,2005,41(12):76-81.
[8]李高林.基于扩展卡尔曼滤波的永磁同步电机的无位置传感器控制[D].长沙:湖南大学,2011.
[9]吴冬敏,邵剑平,芮延年.基于蚁群算法和神经网络的数控机床故障诊断技术研究[J].机械设计与制造,2013,1(1):165-167.
[10]胡三丽.电动车辆锂离子动力电池的SOC预测方法研究[D].广西:广西科技大学,2015.

